



Next: A Random Matrix Theory
Up: Methods
Previous: Analysing returns
Contents
The correlation of stock prices
The correlation coefficient, 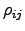 between stocks
between stocks 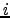 and
and 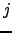 is given by:
is given by:
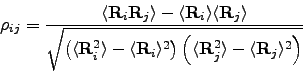 |
(2.6) |
where 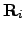 is the vector of the time series of log-returns,
is the vector of the time series of log-returns,
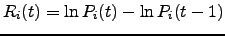 and
and 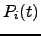 is the daily closure price of stock
is the daily closure price of stock 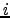 at day
at day 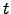 . The notation
. The notation
 means an average over time
means an average over time
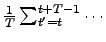 , where
, where 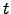 is the first day and
is the first day and 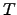 is the length of our time series.
We can normalise the time series of returns for each stock by subtracting the mean and dividing by the standard deviation:
is the length of our time series.
We can normalise the time series of returns for each stock by subtracting the mean and dividing by the standard deviation:
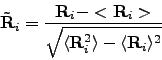 |
(2.7) |
The correlation coefficient is then given by:
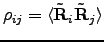 .
.
This coefficient can vary between
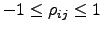 , where
, where 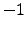 means completely anti-correlated stocks and
means completely anti-correlated stocks and 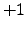 completely correlated stocks. If
completely correlated stocks. If 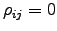 the stocks
the stocks 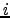 and
and 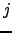 are uncorrelated. The coefficients form a symmetric
are uncorrelated. The coefficients form a symmetric 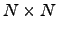 matrix with diagonal elements equal to unity.
The correlation matrix with elements
matrix with diagonal elements equal to unity.
The correlation matrix with elements 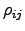 can be represented as:
can be represented as:
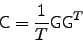 |
(2.8) |
where 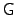 is an
is an 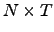 matrix with elements
matrix with elements
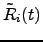 and
and 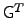 denotes the transpose of
denotes the transpose of 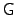 .
.
The distribution of correlation coefficients is an important aspect of our study because can show how the stocks from a portfolio are related with each other. If we compare the distribution of real data with the one made from random data (Figure 3.1), conclusions about the non-randomness of the market can be done. We can also study the moments of this distribution, as the mean [20,25]:
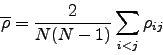 |
(2.9) |
the variance:
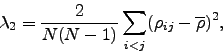 |
(2.10) |
the skewness:
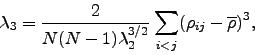 |
(2.11) |
and the kurtosis:
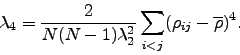 |
(2.12) |
Just the elements of the upper triangle of the matrix are used to compute the matrix, because it's a symmetric matrix with diagonal elements equal to unity. If we divide our time series in small windows and we move these windows in small steps, we create different correlation matrices, and if we compute the moments of each matrix, we can study these moments in time.




Next: A Random Matrix Theory
Up: Methods
Previous: Analysing returns
Contents
Ricardo Coelho
2007-05-08
![]() between stocks
between stocks ![]() and
and ![]() is given by:
is given by:
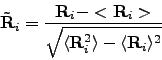
![]() , where
, where ![]() means completely anti-correlated stocks and
means completely anti-correlated stocks and ![]() completely correlated stocks. If
completely correlated stocks. If ![]() the stocks
the stocks ![]() and
and ![]() are uncorrelated. The coefficients form a symmetric
are uncorrelated. The coefficients form a symmetric ![]() matrix with diagonal elements equal to unity.
The correlation matrix with elements
matrix with diagonal elements equal to unity.
The correlation matrix with elements ![]() can be represented as:
can be represented as: