3.5 Rotational transitions in the C60 thin film

The study of phase transitions in two-dimensional (2D) systems is an active area of research due to their potential applications, such as improving the performance of liquid crystal opto-electronic devices [121] and high-T_C superconductors [122, 123], and determining the thermodynamic properties of nanoparticles [124]; and also due to the fundamental physics at play such as the crystal structure of novel intermetallic compounds [125]. There are major differences between phase transitions in 2D and 3D systems [126–129]. For example, melting in 3D crystals is always a first order transition, whereas in 2D systems this is not necessarily the case.

In the close-packed, two-dimensional layer of C60 molecules, individual molecules are weakly bonded to their nearest neighbors. If each molecule in such a monolayer could be addressed individually, this could provide the basis for a device with an ultra-high element density. The properties of such devices are determined by the behavior of both the individual molecules and the C60 layer as a whole.

The unique properties of fullerenes and fullerene-based compounds result from the structure and shape of the C60 molecule. The symmetry of the molecule and its deviations from a uniform spherical shape give it rotational degrees of freedom, which often determine the physical properties of C60 compounds, C60-based clusters, 2D layers and the 3D crystal. At room temperature, C60 molecules arranged in a face-centred cubic lattice (FCC) undergo rapid rotation around their centers of mass. The typical time for a single molecular rotation is in the range of 3 picoseconds [130].

Below 259 K, however, ordering occurs, resulting in a change of space group symmetry from FCC to simple cubic [131–133]. Neutron scattering studies [132, 134] have shown that between 90 K and 259 K, C60 molecules in the 3D crystal shuffle between two nearly degenerate orientations, which differ in energy by 11 meV. The orientations are separated by an energy barrier of 290 meV [135, 136].

There is a glassy transition in the 3D crystal at 90 K, resulting from a freezing of the molecules’ hopping between the two orientations [137]. The relaxation time is estimated to be about 1 day at 90 K [138, 139]. The relaxation process around the glassy transition can be fitted by a non-exponential function exp{−(t∕τ)^β} [137], where β = 0.94 [139]. The deviation of the relaxation dependency from a simple exponential (β = 1) curve provides evidence for significant interaction between the molecules.

The rotational phase transition in an 80 nm, single-crystalline C60 film deposited on GaAs(111) has been previously studied by X-ray diffraction [140]. The results of these measurements reveal an anomaly in the lattice parameter at the phase transition temperature T_C = 240K, 19 K below that of the bulk C60 crystal. This difference was attributed to a strain effect in the C60 film introduced by the substrate.

Mean field theory has been used to model the interactions of solid C60, both at the surface of the crystal and in the bulk, and these calculations have been confirmed by experimental results. In solid C60, melting of the orientational order starts from the top layer of the surface. Lu et al. [138] and Lamoen and Michel [141] have each modelled the interactions in bulk C60 using mean field techniques, and were able to reproduce the experimentally-observed crystal symmetries, including the phase transition from a low-temperature simple cubic structure to a disordered face-centred cubic structure at 260 K.

Passerone and Tosatti [142], and Laforge et al. [143] later built upon these models to describe the rotational surface disordering phase transition for the (111) surface of solid C60, for which three separate phases are predicted and observed. Below 150 K, the surface has (2 × 2) symmetry. Three molecules in the surface (2 × 2) unit cell have only a twofold axis normal to the surface. The fourth, more frustrated molecule has instead its threefold axis normal to the surface. Between 150 K and 230 K, the surface symmetry is still (2 × 2), but the more frustrated molecule begins to rotate, and above 230 K, all surface molecules are in the disordered state, with (1 × 1) surface symmetry.

This section is focused on the link between an individual molecule’s transitions between different states and the phase transition of a statistical ensemble of C60 molecules forming a single molecular layer on the WO2/W(110) surface in the temperature range between 78 K and 320 K. A rotational phase transition at 259 K and a kinetic glassy transition at 220 K have been observed. A good agreement between the parameters of the observed rotational transitions and those predicted from the properties of individual C60 molecules has been found.

3.5.1 Temperature dependence

At low temperatures (below 220 K), STM images of individual molecules reveal an orbital structure that is determined by the orientation of the C60 molecule (Figure 3.12a, b). The arrangement of the molecular orbitals depends on the cooling regime. When the sample was quenched with a cooling rate of 10 K/min, it formed the orbital structure presented in Figure 3.12a. This structure is characterized by a random orientation of C60 molecules forming a glassy, metastable state. No correlations between the individual orientations of neighboring C60 molecules have been found.

The orbital arrangement shown in Figure 3.12b was realized by slowly cooling the film, at a rate of 100 K/day, from 300 K down to 78 K. The molecular orbitals of individual C60 appear in the STM image of the orbital-correlated state as stripes aligned in approximately the same direction (Figure 3.12b). Almost all C60 molecules in Figure 3.12b exhibit this striped structure, which indicates that these molecules face the substrate with an h–h bond [46]. Such an approximate orbital alignment has been observed both along and perpendicular to a close-packed direction of the molecular layer. As the state shown in Figure 3.12b results from slow cooling, it would suggest that the alignment with the h–h bonds facing the substrate has lower energy than the glassy, metastable state obtained by quenching the sample. In this chapter, common notations for states characterized by different bonds between C60 and the surface are used: h, h–h, p, h–p, and s.

At a temperature of 78 K, the majority of the molecules retained their orbital structure and they were static for the duration of the experiment (up to several days), regardless of whether they were in the h–h or h–p state. In contrast, at high temperatures (T > 259K), the orbital structure of individual C60 molecules is no longer visible in STM images (Figure 3.12c) due to the molecules’ rotation, which is faster than the time resolution of the STM. All C60 molecules appear in these STM images as perfect spheres.

At intermediate temperatures (220–259 K), both static and rotating molecules appear in the STM images (Figure 3.12d). In the temperature range 220–259 K the fraction of static molecules rapidly decreases with increasing temperature.

At T < 220K, almost all molecules exhibit the orbital structure. The few anomalies are likely caused by defects on the surface. Figure 3.13 shows the temperature dependence of the square of the probability of finding a static C60 molecule, p², to demonstrate the observed transitions and reveal the order parameter η. Each point in Figure 3.13 corresponds to several large-scale STM images of the C60 film at that temperature (of similar size to Figure 3.12d), and p is calculated by counting the number of static molecules in an image and dividing by the total number of visible molecules.

According to Landau’s theory of phase transitions, the order parameter η is proportional to (T_C −T)^1∕2. At low temperatures (T < 220K), p² is constant with respect to temperature, but does not quite reach unity, since the few molecules close to the defects appearing in the STM images were not included in the number of static molecules. The horizontal blue trend line shown is a fit to the data, with its slope set to 0.

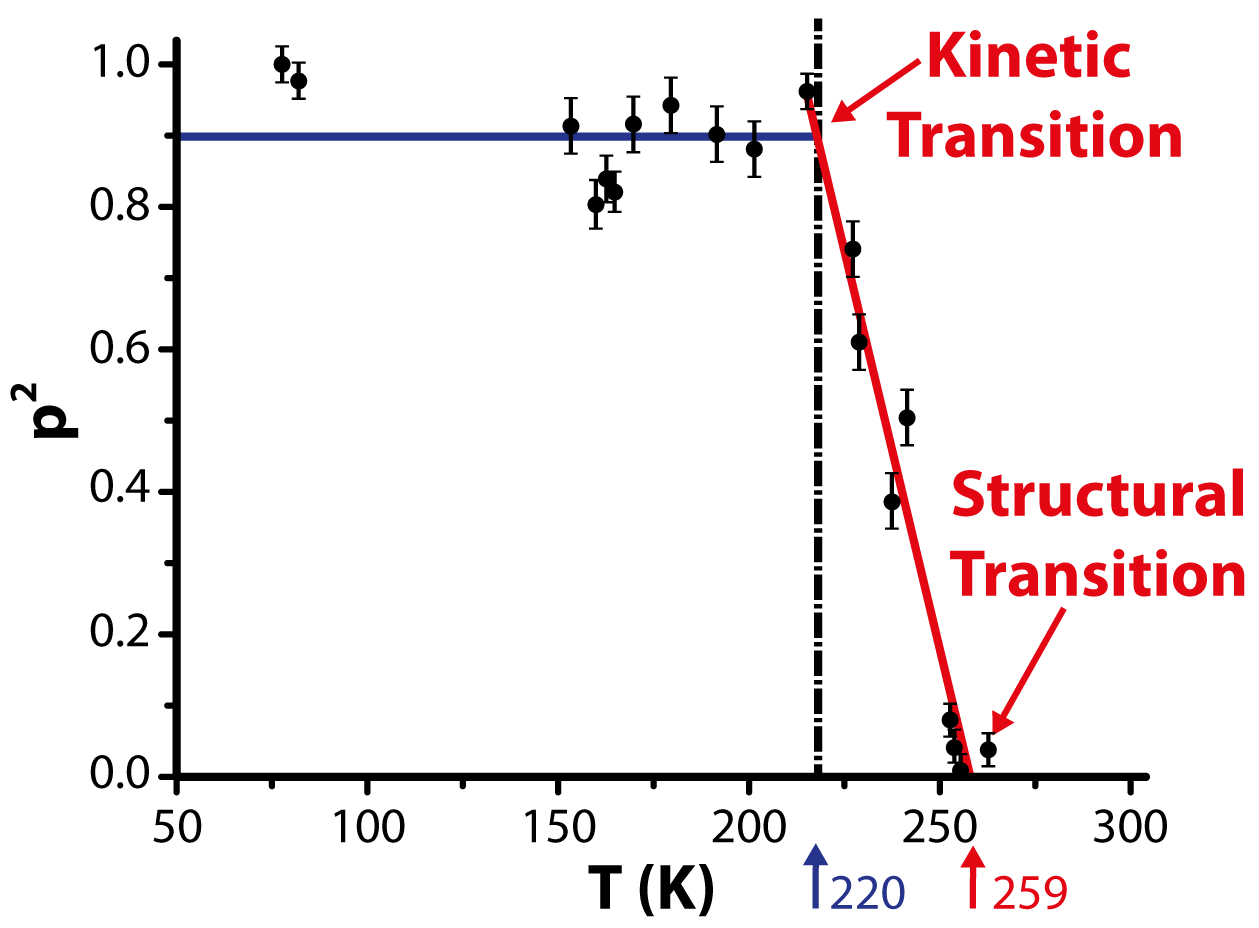
In the temperature range from 220–259 K, p² is fitted by a linear function p² = α(T _C − T), where α = 0.022 ± 0.002K^-1 and T_C = 259K. T_C indicates the temperature of the rotational phase transition. The glassy transition at T_g = 220K is a kinetic transition, at which the molecular switching rate between different states becomes slower than the time scale of the experiment. Below T_g, the C60 molecules’ nanomotion becomes virtually frozen and orbital-resolved STM images of individual molecules do not change.

3.5.2 Molecular transitions between different states

Orbital-resolved STM images of C60 present a unique opportunity to study the rotational transition mechanism on a molecular scale. Figure 3.14 shows a consecutive set of STM images of the C60 monolayer measured at T = 256K, in the vicinity of the rotational phase transition, (T_C − T)∕T_C = 0.012.

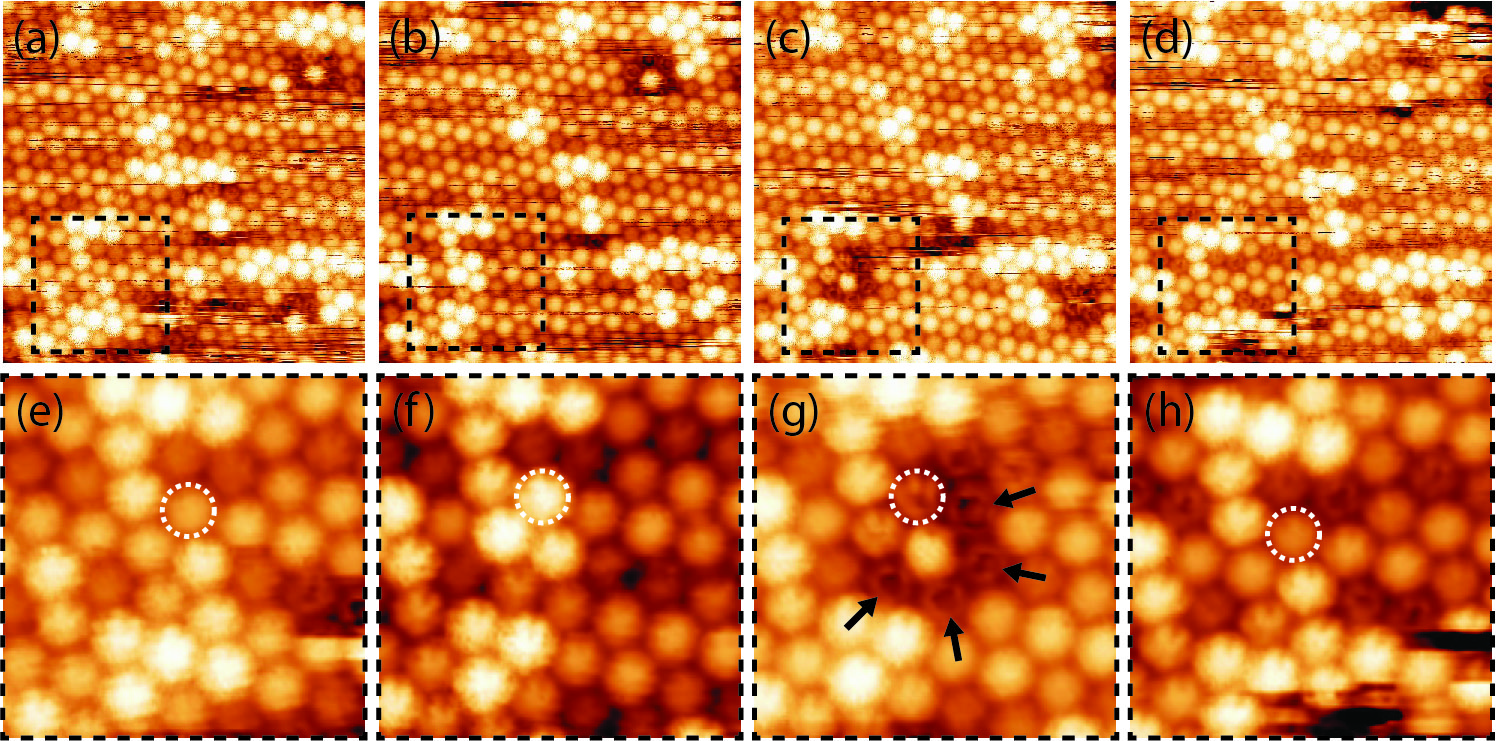
The STM images presented in Figure 3.14a–h indicate how C60 molecules can switch between several different states, leading to changes in their appearance. Some molecules switch between a high- and a low-conductance state, observed in STM images as a repetitive switching between a bright and dark appearance. This will be explored in detail in Section 3.6. Furthermore, static molecules exhibit an orbital structure [46], while those with high-magnitude oscillations and molecular rotation appear blurry in STM images.

Panels e–h show a zoom of the area marked by a dashed box in panels a–d. A single molecule which switches between states in subsequent scans is shown by a dashed circle. The mechanism of a molecule’s switching is connected to its rotation, accompanied by charge transfer to or from the molecule, leading to it becoming polarized [144, 145]. The molecules can also switch between static (orbitals resolved) and dynamic (orbitals blurred) states.

We also observe molecules that appear in the STM images as a ring shape, or a ring with a protrusion at the centre (Figure 3.12c, Figure 3.14e, f, h). Such shapes can be explained by the molecules spinning around their axis perpendicular to the surface. This is shown in detail in Figure 3.17. Arrows in Figure 3.14g indicate several such spinning molecules exhibiting the ring shape appearance. These molecules do not spin in Figure 3.14e or Figure 3.14f.

From the analysis of an extensive number of STM images it was found that, in many cases, the switching of one molecule into a bright state can trigger the spinning of its nearest neighbors. It was also observed that spinning molecules tend to occupy positions along the grooves of the WO2/W(110) substrate, as shown in Fig. 3.15. This suggests that the energy levels of the C60 molecules are affected by the substrate and also that the molecular states can be made more stable or less stable depending on the position of the molecule within the unit cell of the WO2/W(110) structure.

Therefore, in addition to the transition between different orbital states, there are transitions between the static state of the molecule and spinning state (in-plane rotation). Such phenomena are only observed for isolated molecules and molecular clusters in the monolayer, and so are not caused by molecular transfer to the tip or other tip effects, because if that were the case, the tip would affect all molecules being imaged.

3.5.3 DFT calculations of C60 orientation & spinning molecules

DFT was performed using the VASP code and LDA pseudopotentials. The choice of LDA is justified, as it has been shown that DFT-LDA has given excellent results for the total energies and band structures of fullerites and other carbon-based structures (graphite, nanotubes) [146–151].

Girifalco and Hodak state that first-principles calculations for graphitic structures can be carried out quite successfully, but they are sensitive to the details of the calculation, and long-range dispersion interactions, such as van der Waals forces, should be included for separation distances greater than 1.15 of the equilibrium separation [152]. However, the separation distance of C60–C60 on the WO2/W(110) surface is 9.5 ± 0.5 Å, which is less than the intermolecular distance of 10 Å in the bulk C60 crystal. This strongly suggests that van der Waals interactions can be neglected for the system under investigation in this thesis, and that DFT-LDA calculations are sufficient.

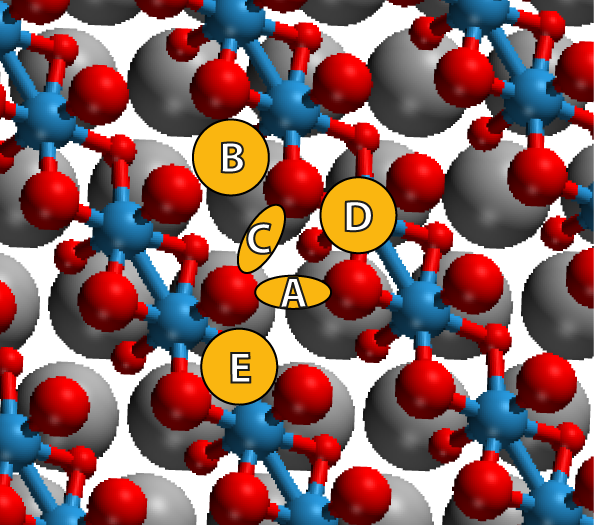
To find the optimum surface site of a single C60 molecule on one layer of WO₂, several different surface sites (labelled A, B, C, D and E in Figure 3.16) were sampled and the total energy of those systems was calculated. The system was found to have the lowest ground state energy when the C60’s surface-facing C–C bond bridged two surface oxygen atoms, each of which was bonded to a different tungsten atom (site A). This site was chosen for all further calculations, and in order to further minimize the energy of the system, different orientations of C60 on this site were simulated. For all orientations, the C60 molecule was allowed to relax on a constrained layer of WO₂.

DFT calculations of the total free energy reveal that the h–h configuration corresponds to the lowest energy state. The h–p configuration is separated from the lowest energy state by 17 meV, which is comparable to k_BT in our STM experiments. The energy gap between the p and the h–h configurations is about 90 meV. The h and s configurations are the least favorable, being separated in energy from the h–h configuration by 360 meV and 420 meV respectively. The partial charge density of each of these systems was calculated in the range from E_F to 1 eV, where E_F is the Fermi energy.

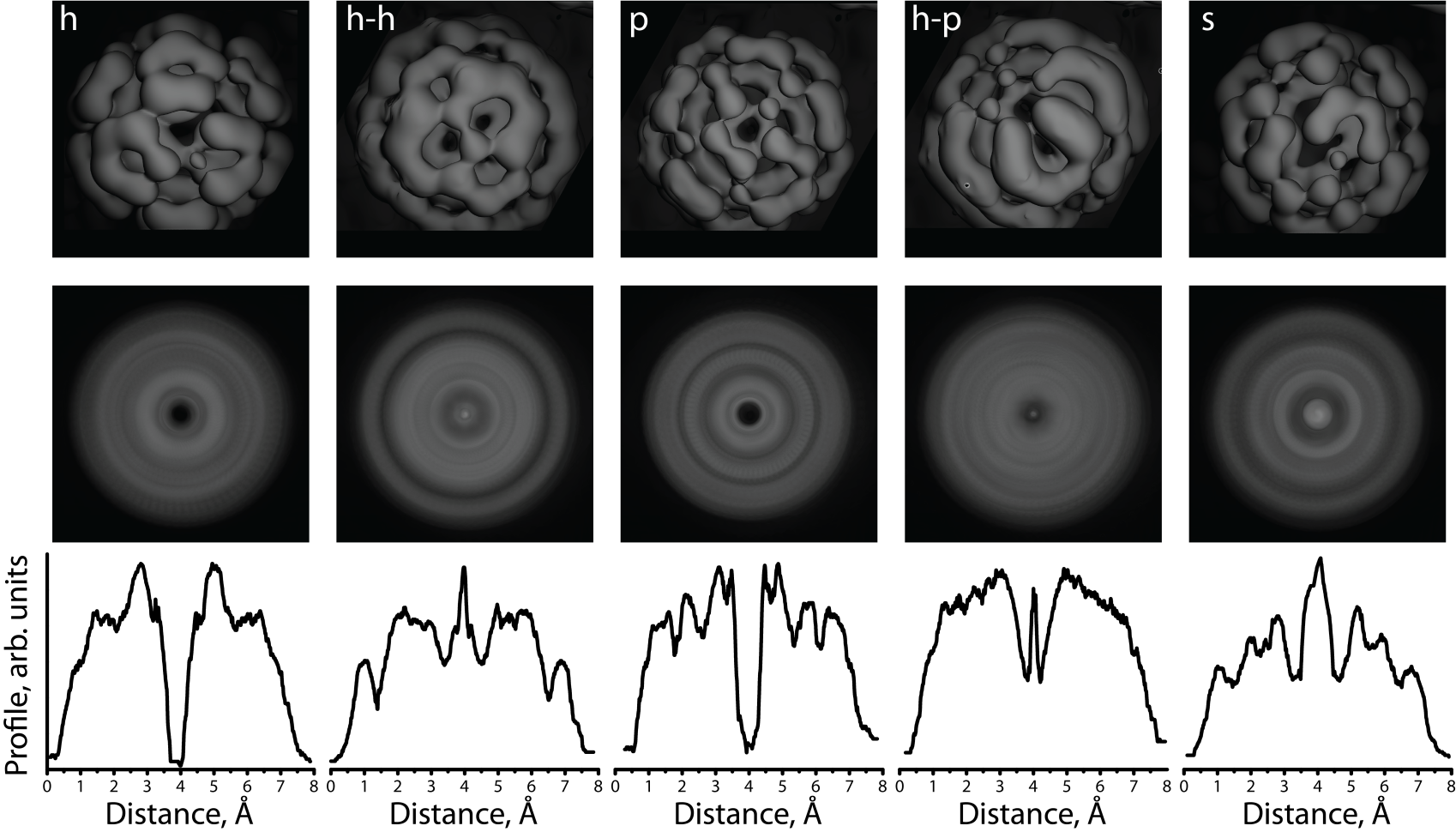
The obtained charge distribution images (Figure 3.17, first row) were then processed by rotating them in increments of 5 degrees. The resulting rotated images (Figure 3.17, second row) were combined to form a single composite weighted image for each orientation. This represents a molecule spinning too fast for the STM probe to resolve. The charge distribution images for h and p orientations reveal a dip at the center of the molecular image while for h–h, h–p and s orientations, the ring shape of the molecule is accompanied by a protrusion at the center. Cross-section profiles of these simulated spinning molecules are shown in Figure 3.17 for comparison with experiment. STM images of individual spinning molecules were found to have either a ring shape with a dip/dent (Figure 3.18a) or a protrusion in the centre (see molecules indicated by black arrows in Figure 3.12c and Figure 3.18c).

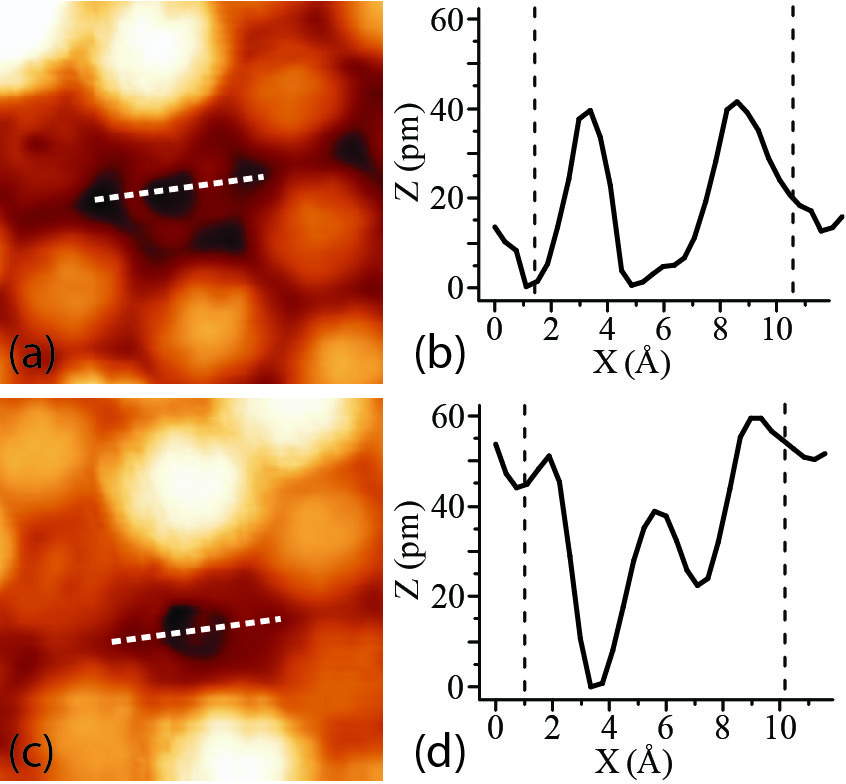
Cross-sections of typical STM images of the spinning C60 molecules are presented in Figure 3.18. Panel (b) corresponds to the dip at the centre while (d) corresponds to the protrusion. About 90% of the examined STM images of spinning C60 molecules reveal a protrusion at the centre of ring shaped images. According to DFT calculations, h–h and h–p orientations are most favorable in energy. Thus, we conclude that most of spinning molecules face the surface by C–C bonds. The STM image presented in Figure 3.18 with a dip at the center of the molecule is most likely due to a spinning molecule with a pentagon facing the substrate.

The peak-to-peak diameter of the holes has been observed to vary between approximately 3–6 Å, and the diameters of the experimental cross-sections in Figure 3.18 are approximately a factor of 2 larger than those calculated in Figure 3.17. This difference, and the distribution of diameters, is attributed to molecular movement on the surface, such as the precession of the spinning axis around the surface normal, for which different precession angles will alter the apparent size of the hole by different amounts. The h and s configurations of the molecules are unlikely to be observed to spin under the present experimental conditions because of the large gap in energy from the ground state. Thus the model suggests that a spinning molecule presents a reasonable explanation for the unusual appearance of the C60 molecules observed in the temperature range of 220–259 K.

3.5.4 Phase transition

In the three-dimensional C60 crystal, two transitions are associated with molecular rotation: a first-order transition that takes place at 259 K and a kinetic glassy transition at 90 K [130–136]. Above 259 K, the molecules freely rotate. At lower temperatures, the molecules hop between two orientations separated in energy by about 11 meV. At 90 K, the C60 crystal undergoes a glassy transition when the equilibrium relaxation time τ exceeds the laboratory experiment time. τ was estimated to change from 1 second to 1 day between 130 K and 90 K, with a relaxation activation energy, W_τ of about 290 meV [138].

We found that at T > 259K, the C60 molecules in the monolayer deposited on the WO2/W(110) surface freely rotate (Figure 3.12d), similar to behaviour observed in solid C60. In contrast, at lower temperatures (T < 259K) we found significant differences between the monolayer and bulk C60. However, it is surprising that the temperature of the rotational phase transition in the C60 monolayer on the WO2/W(110) surface coincides with that of solid C60.

When very close to the phase transition temperature, fluctuations appear in the form of blinking or spinning molecules. Hence, close to T_C there will be inhomogeneity introduced by these fluctuations but not necessarily large regions of instability, similar to how orientational melting begins at the surface of bulk C60 [143]. The amount of these fluctuations decays exponentially away from T_C, and at low temperatures the film looks homogeneous (Figure 3.12b).

According to mean field theory [153], the temperature of a phase transition, T_C = E∕2k_B, is determined by the total energy of interaction between the molecule and its neighbors. In a C60 monolayer, this is determined by the C60’s interaction with its neighboring molecules, the C60–substrate interaction and the crystal field. The interaction between C60 molecules has been studied using several models. Calculations [154, 155] reveal that, in the case of C60 molecules separated by 1 nm, a distance comparable to the separation between molecules’ centres in a monolayer, the dominant contribution is due to the Coulomb interaction between the molecules’ respective charge densities. These calculations show that several combinations of orbital configurations of two adjacent C60 molecules are close in energy.

The coordination number of a C60 molecule in a monolayer is halved to 6, compared to the 12-fold coordinated FCC bulk lattice. Therefore one could simplistically expect a T_C reduced roughly by a factor of two compared to that of the bulk, if the interaction with the substrate was neglected. Such a reduction is indeed observed at the (111) surface of a C60 crystal [143, 156]. In contrast, our experiment shows the same value of T_C = 259K for the C60 monolayer as that of the bulk, suggesting that an energy contribution on the order of k_BT_C = 24meV originates from interactions with the substrate.

There are two possible mechanisms for such an interaction: via the crystal field, which has a strong component perpendicular to the substrate due to the breaking of z-translational invariance [157]; or due to the effect of the overlap of the orbitals of the C60 molecules and the substrate.

The wave function of the HOMO of a single C60 decays out of the molecule over the length scale of a covalent bond (1.4 Å). This is comparable to the distance between the C atoms of an individual C60 molecule and the substrate surface atoms, as determined experimentally (approximately 1.5 Å). The importance of the interaction of C60 with the substrate is confirmed by the decoration of WO2/W(110) grooves by spinning molecules (Figure 3.15d). This suggests that the energy of the C60 is sensitive even to relatively small changes in the environment, such as being brought into closer contact with the substrate due to the WO2/W(110) coincidence structure.

In the mean field theory approximation, the order parameter’s dependence on the temperature is specified as p² ≈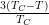 = α(T_C − T), where α = 0.012K^-1. The experimentally-measured value of α = 0.022 ± 0.002K^-1 is approximately a factor of two greater than that predicted by theory. One reason for this discrepancy is that correlation effects are ignored by mean field theory. Examples of such correlation effects that have been observed are presented in Figure 3.12d, where it is shown that static molecules form clusters, and their orientations within the clusters are correlated. This implies that the total energy of a molecule’s interaction with its neighbours is also affected by its configuration on the substrate.

3.5.5 Kinetic transition

The glassy transition and non-exponential relaxation in solid C60 are due to the freezing of weakly-correlated orientations of nearest-neighbor molecules [137]. In bulk C60, the molecules can occupy two rotational orientations which are almost equivalent in energy but are separated by a potential barrier, and these orientations are distributed in a random fashion over the sites of an FCC lattice. The relaxation of solid C60 is determined by the potential barrier between these two states. All individual molecules in solid C60 occupy equivalent positions in the FCC lattice; each molecule relaxes nearly identically in an intrinsically non-exponential manner according to a homogeneous scenario [158].

This relaxation is characterized by the Kohlrausch-Williams-Watts or stretched exponential function, q(t) = q₀  exp[−(t∕τ)^β], where τ is the relaxation time, and β is called the non-exponential factor or “stretching exponent”. β = 1 corresponds to an exponential, Arrhenius-like relaxation [137]. The temperature dependence of τ can be fitted by the Vogel-Fulcher-Tammann (VFT) function, τ(T) = 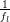  exp[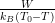], where f_l is the libron frequency [158, 159]. When T₀ = 0K, the Arrhenius equation is realized and W corresponds to the activation energy. According to empirical observations, T₀ corresponds to the temperature of an ideal glass state (“Kauzmann temperature”), at which the crystal and the extrapolated glass state attain equal entropies [159] and the relaxation time becomes infinite.

Both β and 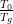are a measure of the deviation from Arrhenius relaxation. The relaxation in solid C60 was found to differ slightly from a purely exponential decay (β = 0.94) [137]. The kinetic behavior of the C60 monolayer grown on the WO2/W(110) surface is influenced by several factors. The low-temperature glassy state of the C60 film is characterized by a random orientation of the molecules (Figure 3.12a). In contrast, the glassy state in solid C60 is characterized by the random freezing of molecules among just two states. The large number of different molecular orientations observed in the film results in an averaging-out of the interaction potentials and should cause Arrhenius-like relaxation processes. However, STM experiments reveal correlations in the nanomotion of the C60 molecules that suggest arguments in favour of a constrain-dynamic scenario [160]. It is proposed that the mechanism for the molecule–molecule interaction required for such a constrain-dynamic scenario can be based on some molecules acquiring charge. Indeed, the time-resolved STM experiments presented herein demonstrate that the rotational transition of an individual C60 molecule between states is accompanied by charge transfer to the molecule, and subsequently, charge carried by a molecule affects the energy levels and barrier heights of its neighboring molecules via the Coulomb interaction.

From the lifetime of a molecule in a single state, the potential barrier height separating the states has been calculated to be 617 meV. If one assumes that the bulk libron frequency of f_l = 1 × 10¹²Hz and the relaxation time at the temperature of glassy transition for solid C60, τ_S(90K) = 1day can be applied to the film, then the VFT law can be used to estimate the Kauzmann temperature T₀. The obtained value T₀ = 45K indicates that the relaxation process in the C60 monolayer film is close to the Arrhenius scenario of 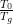= 0.2.