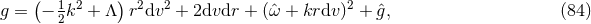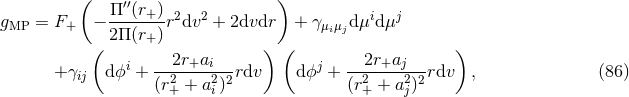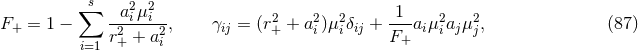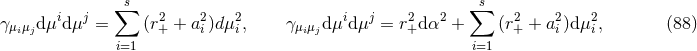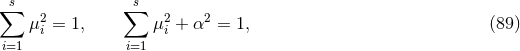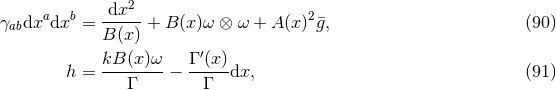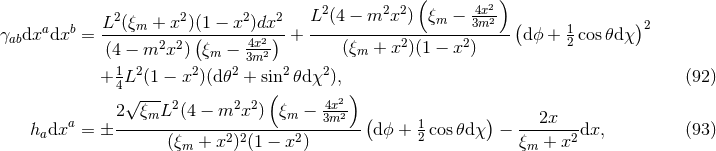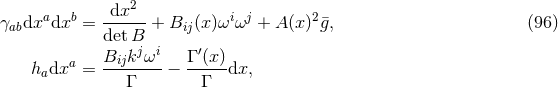4 Vacuum Solutions
The Einstein equations for a near-horizon geometry (7 ) in the absence of matter fields are equivalent to
the following equation on
) in the absence of matter fields are equivalent to
the following equation on 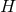 with the function
with the function 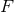 determined by
see Eqs. (17
determined by
see Eqs. (17 ), (18
), (18 ). In this section we will explore solutions to Eq. (66
). In this section we will explore solutions to Eq. (66 ) in various dimensions. It
is useful to note that the contracted Bianchi identity for the horizon metric is equivalent to
) in various dimensions. It
is useful to note that the contracted Bianchi identity for the horizon metric is equivalent to
4.1 Static: all dimensions
A complete classification is possible for 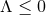 . Recall from Section 3.2.1, the staticity conditions for a
near-horizon geometry are
. Recall from Section 3.2.1, the staticity conditions for a
near-horizon geometry are 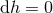 and
and 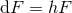 .
.
Theorem 4.1 ([42]). The only vacuum static near-horizon geometry for 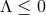 and compact
and compact 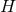 is given by
is given by 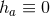 ,
, 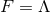 and
and 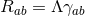 . For
. For 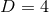 this result is also valid for
this result is also valid for 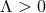 .
.
Proof: A simple proof of the first statement is as follows. Substituting the staticity conditions (50 ) into (67
) into (67 )
gives
)
gives
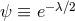 . Irrespective of the topology of
. Irrespective of the topology of 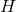 one can argue that
one can argue that 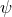 is a globally-defined
function (for simply connected
is a globally-defined
function (for simply connected 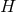 this is automatic, otherwise it can be shown by working in patches on
this is automatic, otherwise it can be shown by working in patches on
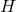 and exploiting the fact that
and exploiting the fact that  in each patch is only defined up to an additive constant). For
in each patch is only defined up to an additive constant). For 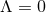 it is then clear that compactness implies
it is then clear that compactness implies 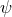 must be a constant. For
must be a constant. For 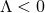 , if one assumes
, if one assumes 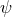 is
non-constant one can easily derive a contradiction by evaluating the above equation at the maximum and
minimum of
is
non-constant one can easily derive a contradiction by evaluating the above equation at the maximum and
minimum of 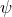 (which must exist by compactness). Hence in either case
(which must exist by compactness). Hence in either case 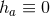 , which gives the claimed
near-horizon data.
, which gives the claimed
near-horizon data.
In four dimensions one can solve Eq. (66 ) in general without assuming compactness of
) in general without assuming compactness of 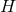 . For
non-constant
. For
non-constant 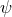 and any
and any 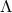 one obtains the near-horizon geometry (sending
one obtains the near-horizon geometry (sending 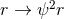 )
)
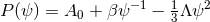 . (This is an analytically-continued Schwarzschild with a cosmological
constant.) This local form of the metric can be used to show that for
. (This is an analytically-continued Schwarzschild with a cosmological
constant.) This local form of the metric can be used to show that for 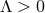 and
and 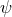 non-constant, there
are also no smooth horizon metrics on a compact
non-constant, there
are also no smooth horizon metrics on a compact 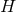 .
.
4.2 Three dimensions
The classification of near-horizon geometries in 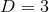 vacuum gravity with a cosmological constant can
be completely solved. Although very simple, to the best of our knowledge this has not been presented
before, so for completeness we include it here.
vacuum gravity with a cosmological constant can
be completely solved. Although very simple, to the best of our knowledge this has not been presented
before, so for completeness we include it here.
The main simplification comes from the fact that cross sections of the horizon 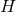 are one-dimensional,
so the horizon equations are automatically ODEs. Furthermore, there is no intrinsic geometry on
are one-dimensional,
so the horizon equations are automatically ODEs. Furthermore, there is no intrinsic geometry on
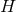 and so the only choice concerns its global topology, which must be either
and so the only choice concerns its global topology, which must be either 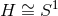 or
or
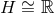 .
.
Theorem 4.2. Consider a near-horizon geometry with compact cross section 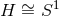 , which
satisfies the vacuum Einstein equations including cosmological constant
, which
satisfies the vacuum Einstein equations including cosmological constant  . If
. If 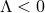 the
near-horizon geometry is given by the quotient of AdS3 in Eq. (73
the
near-horizon geometry is given by the quotient of AdS3 in Eq. (73 ). For
). For 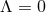 the only solution
is the trivial flat geometry
the only solution
is the trivial flat geometry 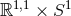 . There are no solutions for
. There are no solutions for 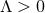 .
.
Proof: We may choose a periodic coordinate 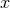 on
on 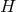 so the horizon metric is simply
so the horizon metric is simply 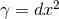 and the
1-form
and the
1-form 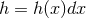 . Observe that
. Observe that 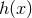 must be a globally-defined function and hence must be a
periodic function of
must be a globally-defined function and hence must be a
periodic function of 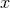 . Since the curvature and metric connection trivially vanish, the horizon
equations (66
. Since the curvature and metric connection trivially vanish, the horizon
equations (66 ) and (67
) and (67 ) simplify to
) simplify to
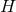 . If
. If 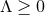 , integrate Eq. (71
, integrate Eq. (71 ) over
) over 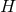 to deduce that
to deduce that 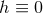 and
and
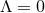 , which gives the trivial flat near-horizon geometry
, which gives the trivial flat near-horizon geometry 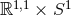 . For
. For 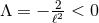 we argue as
follows. Multiply Eq. (71
we argue as
follows. Multiply Eq. (71 ) by
) by 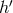 and integrate over
and integrate over 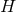 to find
to find 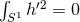 . Hence
. Hence 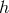 must be a constant and substituting into the horizon equations gives
must be a constant and substituting into the horizon equations gives 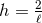 and
and 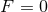 (without loss of generality we have chosen a sign for
(without loss of generality we have chosen a sign for 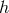 ). The near-horizon geometry is then
This metric is locally AdS3 and in the second equality we have written it as a fibration over
AdS2.
). The near-horizon geometry is then
This metric is locally AdS3 and in the second equality we have written it as a fibration over
AdS2.
It is worth remarking that the ODE (71 ) can be completely integrated without assuming compactness.
For
) can be completely integrated without assuming compactness.
For 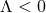 this reveals a second solution
this reveals a second solution 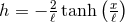 and
and 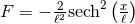 , where we have set
the integration constant to zero by translating the coordinate
, where we have set
the integration constant to zero by translating the coordinate 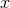 . Upon changing
. Upon changing 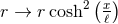 the
resulting near-horizon geometry is:
the
resulting near-horizon geometry is:
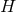 cannot be taken
to be compact and hence we must have
cannot be taken
to be compact and hence we must have 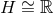 . For
. For 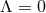 there is also a second
solution given by
there is also a second
solution given by 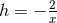 and
and 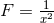 , although this is singular. For
, although this is singular. For 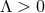 there is
a unique solution given by
there is
a unique solution given by 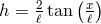 and
and 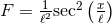 , although this is also
singular.18
, although this is also
singular.18
4.3 Four dimensions
The general solution to Eq. (66 ) is not known in this case. In view of the rigidity theorem it is natural to
assume axisymmetry. If one assumes such a symmetry, the problem becomes of ODE type and it is possible
to completely solve it. The result is summarised by the following theorem, first proved in [122
) is not known in this case. In view of the rigidity theorem it is natural to
assume axisymmetry. If one assumes such a symmetry, the problem becomes of ODE type and it is possible
to completely solve it. The result is summarised by the following theorem, first proved in [122 , 163
, 163 ] for
] for
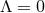 and in [154
and in [154 ] for
] for 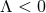 .
.
Theorem 4.3 ([122, 163 , 154
, 154 ]). Consider a spacetime containing a degenerate horizon, invariant
under an
]). Consider a spacetime containing a degenerate horizon, invariant
under an 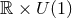 isometry, satisfying the vacuum Einstein equations including a cosmological
constant. Any non-static near-horizon geometry, with compact cross section, is given by the
near-horizon limit of the extremal Kerr or Kerr-(A)dS black hole.
isometry, satisfying the vacuum Einstein equations including a cosmological
constant. Any non-static near-horizon geometry, with compact cross section, is given by the
near-horizon limit of the extremal Kerr or Kerr-(A)dS black hole.
Proof: We present a streamlined version of the proof in [154 ]. As described in Section 3.2.2, axisymmetry
implies one can introduce coordinates on
]. As described in Section 3.2.2, axisymmetry
implies one can introduce coordinates on 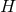 so that
so that
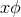 component of Eq. (66
component of Eq. (66 ) implies
) implies 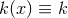 is a constant. The
is a constant. The 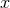 component of Eq. (68
component of Eq. (68 ) then
implies
where
) then
implies
where 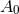 is a constant. Substituting this into Eq. (67
is a constant. Substituting this into Eq. (67 ) gives
Now subtracting the
) gives
Now subtracting the 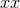 component from the
component from the 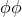 component of Eq. (66
component of Eq. (66 ) gives
A non-static near-horizon geometry must have
) gives
A non-static near-horizon geometry must have 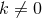 and therefore from the above equation
and therefore from the above equation 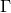 is
non-constant. Using this, one can write Eq. (77
is
non-constant. Using this, one can write Eq. (77 ) as
The solution to the ODE for
) as
The solution to the ODE for 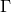 is given by
where
is given by
where 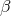 is a positive constant, which can then be used to solve the ODE for
is a positive constant, which can then be used to solve the ODE for 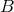 :
where
and
:
where
and 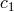 is a constant. Changing affine parameter
is a constant. Changing affine parameter 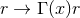 in the full near-horizon geometry finally
gives
with
in the full near-horizon geometry finally
gives
with 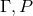 determined above. Observe that this derivation is purely local and does not assume anything
about the topology of
determined above. Observe that this derivation is purely local and does not assume anything
about the topology of 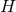 (unlike the derivation in [154
(unlike the derivation in [154 ], which assumed compactness). If
], which assumed compactness). If 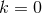 we
recover the general static solution (70
we
recover the general static solution (70 ), hence let us now assume
), hence let us now assume 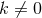 .
.
Now assume 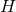 is compact, so by axisymmetry one must have either
is compact, so by axisymmetry one must have either 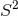 or
or 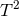 . Integrating
Eq. (77
. Integrating
Eq. (77 ) over
) over 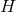 then shows that if
then shows that if 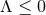 then
then 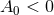 and so the metric in square brackets is AdS2.
The horizon metric extends to a smooth metric on
and so the metric in square brackets is AdS2.
The horizon metric extends to a smooth metric on 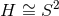 if and only if
if and only if 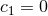 . It can then be checked
the near-horizon geometry is isometric to that of extremal Kerr for
. It can then be checked
the near-horizon geometry is isometric to that of extremal Kerr for 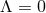 or Kerr-AdS for
or Kerr-AdS for 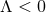 [154
[154 ].
It is also easy to check that for
].
It is also easy to check that for 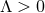 it corresponds to extremal Kerr-dS. In the non-static case, the
horizon topology theorem excludes the possibility of
it corresponds to extremal Kerr-dS. In the non-static case, the
horizon topology theorem excludes the possibility of 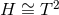 for
for 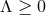 . If
. If 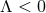 the non-static
possibility with
the non-static
possibility with 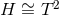 can also be excluded [164
can also be excluded [164 ].
].
It would be interesting to remove the assumption of axisymmetry in the above theorem. In [145] it is
shown that regular non-axisymmetric linearised solutions of Eq. (66 ) about the extremal Kerr near-horizon
geometry do not exist. This supports the conjecture that any smooth solution of Eq. (66
) about the extremal Kerr near-horizon
geometry do not exist. This supports the conjecture that any smooth solution of Eq. (66 ) on
) on 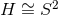 must be axisymmetric and hence given by the above theorem.
must be axisymmetric and hence given by the above theorem.
4.4 Five dimensions
In this case there are several different symmetry assumptions one could make. Classifications are known for
homogeneous horizons and horizons invariant under a 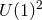 -rotational symmetry.
-rotational symmetry.
We may define a homogeneous near-horizon geometry to be one for which the Riemannian manifold
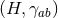 is a homogeneous space whose transitive isometry group
is a homogeneous space whose transitive isometry group 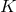 also leaves the rest of
the near-horizon data
also leaves the rest of
the near-horizon data 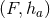 invariant. Since any near-horizon geometry (7
invariant. Since any near-horizon geometry (7 ) possesses the
2D symmetry generated by
) possesses the
2D symmetry generated by 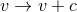 and
and 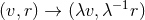 where
where 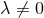 , it is clear
that this definition guarantees the near-horizon geometry itself is a homogeneous spacetime.
Conversely, if the near-horizon geometry is a homogeneous spacetime, then any cross section
, it is clear
that this definition guarantees the near-horizon geometry itself is a homogeneous spacetime.
Conversely, if the near-horizon geometry is a homogeneous spacetime, then any cross section
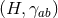 must be a homogeneous space under a subgroup
must be a homogeneous space under a subgroup 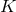 of the spacetime isometry group,
which commutes with the 2D symmetry in the
of the spacetime isometry group,
which commutes with the 2D symmetry in the 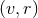 plane (since
plane (since 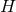 is a constant
is a constant 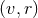 submanifold). It follows that
submanifold). It follows that 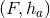 must also be invariant under the isometry
must also be invariant under the isometry 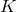 , showing that
our original definition is indeed equivalent to the near-horizon geometry being a homogeneous
spacetime.
, showing that
our original definition is indeed equivalent to the near-horizon geometry being a homogeneous
spacetime.
Homogeneous geometries can be straightforwardly classified without assuming compactness of 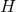 as
follows.
as
follows.
Theorem 4.4 ([158 ]). Any vacuum, homogeneous, non-static near-horizon geometry is locally isometric to
]). Any vacuum, homogeneous, non-static near-horizon geometry is locally isometric to
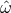 is a
is a 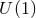 -connection over a 2D base space satisfying
-connection over a 2D base space satisfying 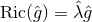 with
with 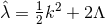 . The
curvature of the connection is
. The
curvature of the connection is 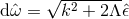 , where
, where 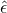 is the volume form of the 2D base, and
is the volume form of the 2D base, and
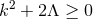 .
.
The proof uses the fact that homogeneity implies 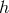 must be a Killing field and then one reduces the
problem onto the 2D orbit space. Observe that for
must be a Killing field and then one reduces the
problem onto the 2D orbit space. Observe that for 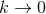 one recovers the static near-horizon
geometries. For
one recovers the static near-horizon
geometries. For 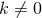 and
and 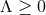 we see that
we see that 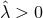 so that the 2D metric
so that the 2D metric 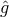 is a round
is a round
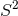 and the horizon metric is locally isometric to a homogeneously squashed
and the horizon metric is locally isometric to a homogeneously squashed 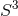 . Hence we
have:
. Hence we
have:
Corollary 4.1. Any vacuum, homogeneous, non-static near-horizon geometry is locally isometric
to the near-horizon limit of the extremal Myers–Perry black hole with 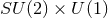 rotational
symmetry (i.e., equal angular momenta). For
rotational
symmetry (i.e., equal angular momenta). For 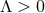 one gets the same result with the Myers–Perry
black hole replaced by its generalisation with a cosmological constant [129
one gets the same result with the Myers–Perry
black hole replaced by its generalisation with a cosmological constant [129 ].
].
For 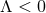 we see that there are more possibilities depending on the sign of
we see that there are more possibilities depending on the sign of 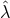 . If
. If 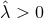 we again
have a horizon geometry locally isometric to a homogeneous
we again
have a horizon geometry locally isometric to a homogeneous 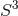 . If
. If 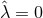 , we can write
, we can write 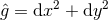 and the
and the 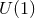 -connection
-connection 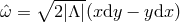 is non-trivial, so the cross sections
is non-trivial, so the cross sections  are the Nil
group manifold with its standard homogeneous metric. For
are the Nil
group manifold with its standard homogeneous metric. For  , we can write
, we can write  and the connection
and the connection 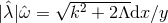 , so the cross sections
, so the cross sections 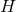 are the
are the 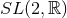 group manifold
with its standard homogeneous metric, unless
group manifold
with its standard homogeneous metric, unless 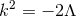 , which gives
, which gives 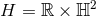 . Hence we
have:
. Hence we
have:
Corollary 4.2. For 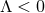 any vacuum, homogeneous, non-static near-horizon geometry is
locally isometric to either the near-horizon limit of the extremal rotating black hole [129
any vacuum, homogeneous, non-static near-horizon geometry is
locally isometric to either the near-horizon limit of the extremal rotating black hole [129 ] with
] with
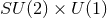 rotational symmetry, or a near-horizon geometry with: (i)
rotational symmetry, or a near-horizon geometry with: (i) 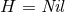 and its
standard homogenous metric, (ii)
and its
standard homogenous metric, (ii) 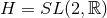 and its standard homogeneous metric or (iii)
and its standard homogeneous metric or (iii)
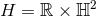 .
.
This is analogous to a classification first obtained for supersymmetric near-horizon geometries in gauged supergravity, see Proposition (5.3).
We now consider a weaker symmetry assumption, which allows for inhomogeneous horizons. A
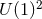 -rotational isometry is natural in five dimensions and all known explicit black-hole solutions have
this symmetry. The following classification theorem has been derived:
-rotational isometry is natural in five dimensions and all known explicit black-hole solutions have
this symmetry. The following classification theorem has been derived:
Theorem 4.5 ([152 ]). Consider a vacuum non-static near-horizon geometry with a
]). Consider a vacuum non-static near-horizon geometry with a 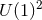 -rotational
isometry and a compact cross section
-rotational
isometry and a compact cross section 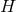 . It must be globally isometric to the near-horizon geometry of one
of the following families of black-hole solutions:
. It must be globally isometric to the near-horizon geometry of one
of the following families of black-hole solutions:
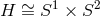 : the 3-parameter boosted extremal Kerr string.
: the 3-parameter boosted extremal Kerr string.
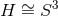 : the 2-parameter extremal Myers–Perry black hole or the 3-parameter ‘fast’ rotating
extremal KK black hole [190
: the 2-parameter extremal Myers–Perry black hole or the 3-parameter ‘fast’ rotating
extremal KK black hole [190 ].
].
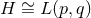 : the Lens space quotients of the above
: the Lens space quotients of the above 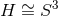 solutions.
solutions.
Remarks:
- The near-horizon geometry of the vacuum extremal black ring [187] is a 2-parameter subfamily
of case 1, corresponding to a Kerr string with vanishing tension [162
 ].
].
- The near-horizon geometry of the ‘slowly’ rotating extremal KK black hole [190] is identical to that of the 2-parameter extremal Myers–Perry in case 2.
- The
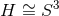 cases can be written as a single 3-parameter family of near-horizon
geometries [135
cases can be written as a single 3-parameter family of near-horizon
geometries [135 ].
].
- The
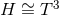 case has been ruled out [131
case has been ruled out [131 ].
].
For 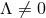 , the analogous problem has not been solved. The only known solution in this case is the
, the analogous problem has not been solved. The only known solution in this case is the 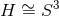 near-horizon geometry of the rotating black hole with a cosmological constant [129], which generalises
the Myers–Perry black hole. It would be interesting to classify near-horizon geometries with
near-horizon geometry of the rotating black hole with a cosmological constant [129], which generalises
the Myers–Perry black hole. It would be interesting to classify near-horizon geometries with
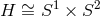 in this case since this would capture the near-horizon geometry of the yet-to-be-found
asymptotically-AdS5 black ring. A perturbative attempt at constructing such a solution is discussed in
[152].
in this case since this would capture the near-horizon geometry of the yet-to-be-found
asymptotically-AdS5 black ring. A perturbative attempt at constructing such a solution is discussed in
[152].
4.5 Higher dimensions
For spacetime dimension 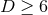 , so the horizon cross section dim
, so the horizon cross section dim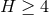 , the horizon equation (66
, the horizon equation (66 ) is
far less constraining than in lower dimensions. Few general classification results are known, although several
large families of vacuum near-horizon geometries have been constructed.
) is
far less constraining than in lower dimensions. Few general classification results are known, although several
large families of vacuum near-horizon geometries have been constructed.
4.5.1 Weyl solutions
The only known classification result for vacuum 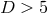 near-horizon geometries is for
near-horizon geometries is for 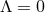 solutions
with
solutions
with 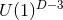 -rotational symmetry. These generalise the
-rotational symmetry. These generalise the 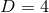 axisymmetric solutions and
axisymmetric solutions and 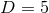 solutions with
solutions with 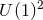 -symmetry discussed in Sections 4.3 and 4.4 respectively. By performing a detailed
study of the orbit spaces
-symmetry discussed in Sections 4.3 and 4.4 respectively. By performing a detailed
study of the orbit spaces 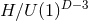 it has been shown that the only possible topologies for
it has been shown that the only possible topologies for 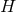 are:
are:
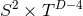 ,
, 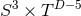 ,
, 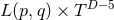 , and
, and 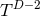 [139
[139 ].
].
An explicit classification of the possible near-horizon geometries (for the non-toroidal case) was derived
in [135 ], see their Theorem 1. Using their theorem it is easy to show that the most general solution with
], see their Theorem 1. Using their theorem it is easy to show that the most general solution with
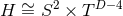 is in fact isometric to the near-horizon geometry of a boosted extremal Kerr-membrane
(i.e., perform a general boost of Kerr
is in fact isometric to the near-horizon geometry of a boosted extremal Kerr-membrane
(i.e., perform a general boost of Kerr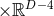 along the
along the 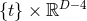 coordinates and then compactify
coordinates and then compactify
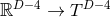 ). Non-static near-horizon geometries with
). Non-static near-horizon geometries with 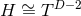 have been ruled out [131]
(including a cosmological constant).
have been ruled out [131]
(including a cosmological constant).
4.5.2 Myers–Perry metrics
The Myers–Perry (MP) black-hole solutions [183] generically have isometry groups 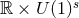 where
where
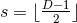 . Observe that if
. Observe that if 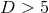 then
then 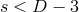 and hence these solutions fall outside the
classification discussed in Section 4.5.1. They are parameterised by their mass parameter
and hence these solutions fall outside the
classification discussed in Section 4.5.1. They are parameterised by their mass parameter 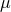 and
angular momentum parameters
and
angular momentum parameters 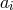 for
for 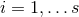 . The topology of the horizon cross section
. The topology of the horizon cross section
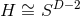 . A generalisation of these metrics with non-zero cosmological constant has been
found [99
. A generalisation of these metrics with non-zero cosmological constant has been
found [99 ]. We will focus on the
]. We will focus on the 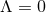 case, although analogous results hold for the
case, although analogous results hold for the 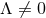 solutions.
solutions.
The location of the horizon is determined by the largest positive number 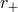 such that
in odd and even dimensions
such that
in odd and even dimensions 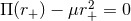 and
and 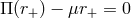 , respectively, where
, respectively, where
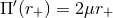 and
and
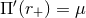 , respectively. These conditions hold only when the black hole is spinning in all the two planes
available, i.e., we need
, respectively. These conditions hold only when the black hole is spinning in all the two planes
available, i.e., we need 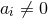 for all
for all 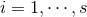 . Without loss of generality we will henceforth
assume
. Without loss of generality we will henceforth
assume 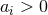 and use the extremality condition to eliminate the mass parameter
and use the extremality condition to eliminate the mass parameter 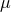 . The
near-horizon geometry of the extremal MP black holes can be written in a unified form [79
. The
near-horizon geometry of the extremal MP black holes can be written in a unified form [79 ]:
where
and in odd and even dimensions
respectively. The direction cosines
]:
where
and in odd and even dimensions
respectively. The direction cosines 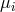 and
and 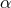 take values in the range
take values in the range 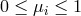 with
with 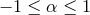 and in odd and even dimensions satisfy
respectively. The generalisation of these near-horizon geometries for
and in odd and even dimensions satisfy
respectively. The generalisation of these near-horizon geometries for 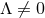 was given in [165]. It is worth
noting that if subsets of the angular momentum parameters
was given in [165]. It is worth
noting that if subsets of the angular momentum parameters 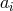 are set equal, the rotational symmetry
enhances to a non-Abelian unitary group.
are set equal, the rotational symmetry
enhances to a non-Abelian unitary group.
Since these are vacuum solutions one can trivially add flat directions to generate new solutions. For
example, by adding one flat direction one can generate a boosted MP string, whose near-horizon geometries
have 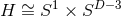 topology. Interestingly, for odd dimensions
topology. Interestingly, for odd dimensions 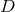 the resulting geometry has
the resulting geometry has 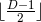 commuting rotational isometries. For this reason, it was conjectured that a special case of this is also the
near-horizon geometry of yet-to-be-found asymptotically-flat black rings (as is known to be the case in five
dimensions) [79].
commuting rotational isometries. For this reason, it was conjectured that a special case of this is also the
near-horizon geometry of yet-to-be-found asymptotically-flat black rings (as is known to be the case in five
dimensions) [79].
4.5.3 Exotic topology horizons
Despite the absence of explicit  black-hole solutions, a number of solutions to Eq. (66
black-hole solutions, a number of solutions to Eq. (66 ) are known.
It is an open problem as to whether there are corresponding black-hole solutions to these near-horizon
geometries.
) are known.
It is an open problem as to whether there are corresponding black-hole solutions to these near-horizon
geometries.
All the constructions given below employ the following data. Let 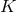 be a compact Fano Kähler–Einstein
manifold19
of complex dimension
be a compact Fano Kähler–Einstein
manifold19
of complex dimension  and
and 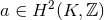 is the indivisible class given by
is the indivisible class given by 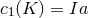 with
with 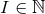 (the Fano index
(the Fano index 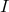 and satisfies
and satisfies 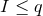 with equality iff
with equality iff 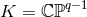 ). The
Kähler–Einstein metric
). The
Kähler–Einstein metric 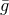 on
on 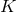 is normalised as
is normalised as 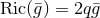 and we denote its isometry
group by
and we denote its isometry
group by 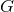 . The simplest example occurs for
. The simplest example occurs for 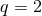 , in which case
, in which case 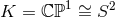 with
with
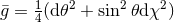 .
.
In even dimensions greater than four, an infinite class of near-horizon geometries is revealed by the following result.
Proposition 4.1 ([156 ]). Let
]). Let 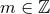 and
and 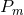 be the principal
be the principal 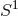 -bundle over any Fano
Kähler–Einstein manifold
-bundle over any Fano
Kähler–Einstein manifold 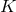 , specified by the characteristic class
, specified by the characteristic class 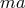 . For each
. For each 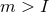 there exists a 1-parameter family of smooth solutions to Eq. (66
there exists a 1-parameter family of smooth solutions to Eq. (66 ) on the associated
) on the associated 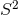 -bundles
-bundles
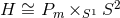 .
.
The dim 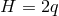 ansatz used for the near-horizon data is the
ansatz used for the near-horizon data is the 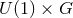 invariant form
invariant form
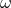 is a
is a 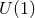 -connection over
-connection over 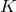 with curvature
with curvature 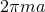 . The solutions depend on one
continuous parameter
. The solutions depend on one
continuous parameter 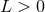 and the integer
and the integer 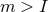 . The continuous parameter corresponds to
the angular momentum
. The continuous parameter corresponds to
the angular momentum ![J [∂ ] ϕ](article975x.gif) where
where 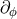 generates the
generates the 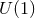 -isometry in the
-isometry in the 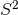 -fibre.
The various functions are given by
-fibre.
The various functions are given by 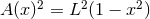 ,
, 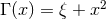 ,
, 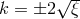 and
and
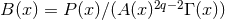 where
where 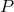 is a polynomial in
is a polynomial in 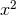 and smoothness fixes
and smoothness fixes 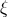 to be a
function of
to be a
function of 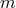 .
.
The simplest example is the 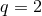 ,
, 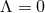 solution, for which the near-horizon data takes the explicit
form
solution, for which the near-horizon data takes the explicit
form
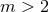 . The coordinate ranges are
. The coordinate ranges are 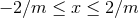 ,
, 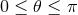 ,
, 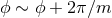 ,
,
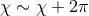 . Cross sections of the horizon
. Cross sections of the horizon 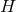 , are homeomorphic to
, are homeomorphic to 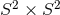 if
if 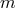 is even,
or the non-trivial bundle
is even,
or the non-trivial bundle 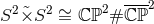 if
if 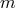 is odd. For
is odd. For 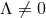 the solutions are
analogous.
the solutions are
analogous.
For 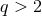 the Fano base
the Fano base 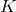 is higher dimensional and there are more choices available. The topology
of the total space is always a non-trivial
is higher dimensional and there are more choices available. The topology
of the total space is always a non-trivial 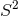 -bundle over
-bundle over 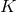 and in fact different
and in fact different 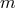 give different
topologies, so there are an infinite number of horizon topologies allowed. Furthermore, one can choose
give different
topologies, so there are an infinite number of horizon topologies allowed. Furthermore, one can choose 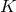 to have no continuous isometries giving examples of near-horizon geometries with a single
to have no continuous isometries giving examples of near-horizon geometries with a single 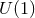 -rotational
isometry. Hence, if there are black holes corresponding to these horizon geometries they would saturate the
lower bound in the rigidity theorem.
-rotational
isometry. Hence, if there are black holes corresponding to these horizon geometries they would saturate the
lower bound in the rigidity theorem.
It is worth noting that the local form of the above class of near-horizon metrics includes as a special case
that of the extremal MP metrics 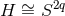 with equal angular momenta (for
with equal angular momenta (for 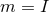 ). The above class of
horizon geometries are of the same form as the Einstein metrics on complex line bundles [186],
which in four dimensions corresponds to the Page metric [185
). The above class of
horizon geometries are of the same form as the Einstein metrics on complex line bundles [186],
which in four dimensions corresponds to the Page metric [185 ], although we may of course set
], although we may of course set
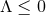 .
.
Similar constructions of increasing complexity can be made in odd dimensions, again revealing an infinite class of near-horizon geometries.
Proposition 4.2. Let 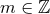 and
and 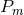 be the principal
be the principal 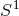 -bundle over
-bundle over 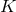 specified by the
characteristic class
specified by the
characteristic class 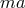 . There exists a 1-parameter family of Sasakian solutions to Eq. (66
. There exists a 1-parameter family of Sasakian solutions to Eq. (66 ) on
) on
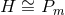 .
.
As a simple example consider 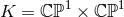 . This leads to an explicit homogeneous near-horizon
geometry with
. This leads to an explicit homogeneous near-horizon
geometry with
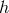 is a vector field,
is a vector field, 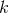 is a constant and
is a constant and 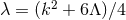 .
Regularity requires that the Chern number
.
Regularity requires that the Chern number 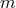 of the
of the 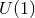 -fibration over each
-fibration over each 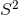 to be the same and
the period
to be the same and
the period 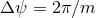 . The total space is a Lens space
. The total space is a Lens space 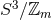 -bundle over
-bundle over 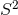 and is topologically
and is topologically
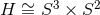 . For
. For  and
and 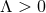 this corresponds to a Sasaki–Einstein metric on
this corresponds to a Sasaki–Einstein metric on 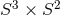 sometimes known as
sometimes known as 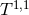 .
.
The above proposition can be generalised as follows.
Proposition 4.3 ([158]). Given any Fano Kähler–Einstein manifold 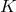 of complex dimension
of complex dimension
 and coprime
and coprime 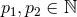 satisfying
satisfying 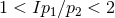 , there exists a 1-parameter family of
solutions to Eq. (66
, there exists a 1-parameter family of
solutions to Eq. (66 ) where
) where 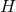 is a compact Sasakian
is a compact Sasakian 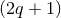 -manifold.
-manifold.
These examples have 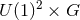 symmetry, although possess only one independent angular
momentum along the
symmetry, although possess only one independent angular
momentum along the 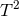 -fibres. These are deformations of the Sasaki–Einstein
-fibres. These are deformations of the Sasaki–Einstein 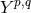 manifolds [94].
manifolds [94].
There also exist a more general class of non-Sasakian horizons in odd dimensions.
Proposition 4.4 ([157 ]). Let
]). Let
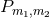 be the principal
be the principal 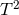 -bundle over any Fano Kähler–Einstein manifold
-bundle over any Fano Kähler–Einstein manifold 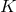 , specified by
the characteristic classes
, specified by
the characteristic classes 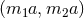 where
where 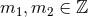 . For a countably infinite set of non-zero
integers
. For a countably infinite set of non-zero
integers 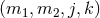 , there exists a two-parameter family of smooth solutions to Eq. (66
, there exists a two-parameter family of smooth solutions to Eq. (66 ) on the
associated Lens space bundles
) on the
associated Lens space bundles 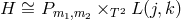 .
.
The dim 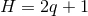 form of the near-horizon data in the previous two propositions is the
form of the near-horizon data in the previous two propositions is the
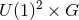 invariant form
invariant form
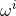 is a principal
is a principal 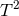 -connection over
-connection over 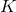 whose curvature is
whose curvature is 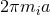 . The explicit
functions
. The explicit
functions 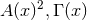 are linear in
are linear in 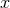 and
and 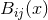 are ratios of various polynomials in
are ratios of various polynomials in 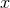 .
Generically these solutions possess two independent angular momenta along the
.
Generically these solutions possess two independent angular momenta along the 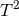 -fibres. The
Sasakian horizon geometries of Proposition 4.3 arise as a special case with
-fibres. The
Sasakian horizon geometries of Proposition 4.3 arise as a special case with 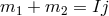 and possess only one independent angular momentum. The base
and possess only one independent angular momentum. The base 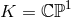 gives horizon
topologies
gives horizon
topologies 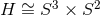 or
or 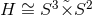 depending on whether
depending on whether 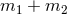 is even or odd
respectively.
is even or odd
respectively.
It is worth noting that the local form of this class of near-horizon metrics includes as a special case that
of the extremal MP metrics 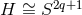 with all but one equal angular momenta. The above class of
horizon geometries are of the same form as the Einstein metrics found in [37, 157
with all but one equal angular momenta. The above class of
horizon geometries are of the same form as the Einstein metrics found in [37, 157 ].
].



![b b ∇aF − F ha − 2h ∇ [ahb] + ∇ ∇ [ahb] = 0. (68 )](article696x.gif)

![dψ2 g = ψ2[A0r2dv2 + 2dvdr ] + ------+ P (ψ)dχ2, (70 ) P (ψ )](article724x.gif)

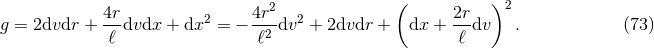
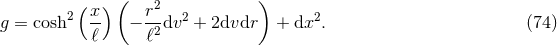
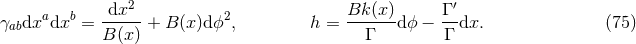






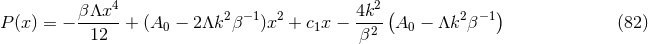
![2 2 Γ (x) 2 P (x) 2 g = Γ (x)[A0r dv + 2dvdr ] + P(x-)dx + Γ-(x-)(dϕ + krdv ) , (83 )](article802x.gif)