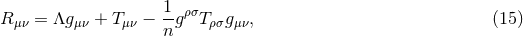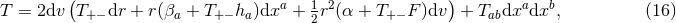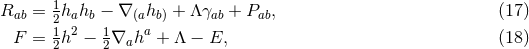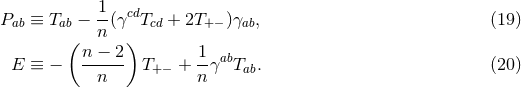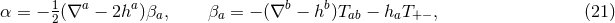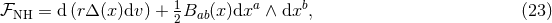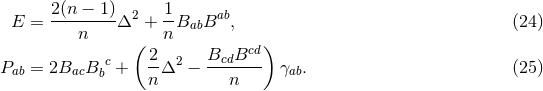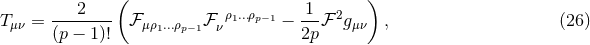2 Degenerate Horizons and Near-Horizon Geometry
2.1 Coordinate systems and near-horizon limit
In this section we will introduce a general notion of a near-horizon geometry.
This requires us to first introduce some preliminary constructions. Let 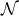 be a
smooth9
codimension-1 null hypersurface in a
be a
smooth9
codimension-1 null hypersurface in a 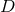 dimensional spacetime
dimensional spacetime 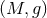 . In a neighbourhood of any such
hypersurface there exists an adapted coordinate chart called Gaussian null coordinates that we now
recall [179
. In a neighbourhood of any such
hypersurface there exists an adapted coordinate chart called Gaussian null coordinates that we now
recall [179 , 86].
, 86].
Let 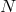 be a vector field normal to
be a vector field normal to  whose integral curves are future-directed null geodesic
generators of
whose integral curves are future-directed null geodesic
generators of  . In general these will be non-affinely parameterised so on
. In general these will be non-affinely parameterised so on  we have
we have 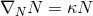 for
some function
for
some function  . Now let
. Now let 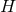 denote a smooth
denote a smooth 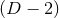 -dimensional spacelike submanifold of
-dimensional spacelike submanifold of 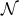 ,
such that each integral curve of
,
such that each integral curve of 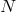 crosses
crosses 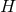 exactly once: we term
exactly once: we term 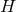 a cross section of
a cross section of 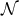 and
assume such submanifolds exist. On
and
assume such submanifolds exist. On 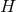 choose arbitrary local coordinates
choose arbitrary local coordinates 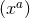 , for
, for 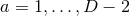 ,
containing some point
,
containing some point 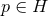 . Starting from
. Starting from 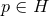 , consider the point in
, consider the point in 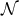 a parameter value
a parameter value  along the integral curve of
along the integral curve of 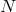 . Now assign coordinates
. Now assign coordinates 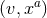 to such a point, i.e., we extend the
functions
to such a point, i.e., we extend the
functions 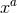 into
into 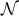 by keeping them constant along such a curve. This defines a set of coordinates
by keeping them constant along such a curve. This defines a set of coordinates
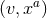 in a tubular neighbourhood of the integral curves of
in a tubular neighbourhood of the integral curves of 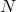 through
through 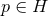 , such that
, such that
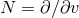 . Since
. Since 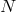 is normal to
is normal to 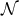 we have
we have 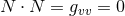 and
and 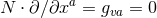 on
on
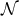 .
.
We now extend these coordinates into a neighbourhood of 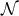 in
in 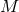 as follows. For any point
as follows. For any point
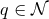 contained in the above coordinates
contained in the above coordinates 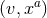 , let
, let 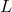 be the unique past-directed null vector
satisfying
be the unique past-directed null vector
satisfying 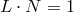 and
and 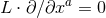 . Now starting at
. Now starting at 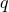 , consider the point in
, consider the point in 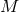 an affine
parameter value
an affine
parameter value  along the null geodesic with tangent vector
along the null geodesic with tangent vector 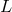 . Define the coordinates of such a point
in
. Define the coordinates of such a point
in 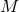 by
by 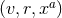 , i.e., the functions
, i.e., the functions 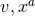 are extended into
are extended into 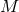 by requiring them to be constant
along such null geodesics. This provides coordinates
by requiring them to be constant
along such null geodesics. This provides coordinates 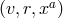 defined in a neighbourhood of
defined in a neighbourhood of 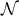 in
in 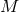 ,
as required.
,
as required.
We extend the definitions of 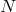 and
and 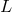 into
into 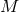 by
by 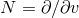 and
and 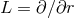 . By construction
the integral curves of
. By construction
the integral curves of 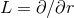 are null geodesics and hence
are null geodesics and hence 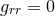 everywhere in the neighbourhood
of
everywhere in the neighbourhood
of 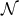 in
in 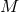 in question. Furthermore, using the fact that
in question. Furthermore, using the fact that 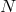 and
and 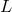 commute (they are coordinate
vector fields), we have
commute (they are coordinate
vector fields), we have
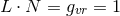 for all
for all  . A similar argument shows
. A similar argument shows 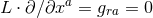 for all
for all
 .
.
These considerations show that, in a neighbourhood of  in
in  , the spacetime metric
, the spacetime metric  written in
Gaussian null coordinates
written in
Gaussian null coordinates  is of the form
is of the form
 is the hypersurface
is the hypersurface 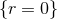 , the metric components
, the metric components 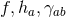 are smooth functions of all the
coordinates, and
are smooth functions of all the
coordinates, and 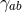 is an invertible
is an invertible 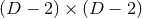 matrix. This coordinate chart is unique up to
choice of cross section
matrix. This coordinate chart is unique up to
choice of cross section 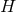 and choice of coordinates
and choice of coordinates 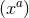 on
on 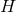 . Upon a change of coordinates on
. Upon a change of coordinates on 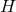 the quantities
the quantities 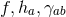 transform as a function, 1-form and non-degenerate metric, respectively. Hence
they may be thought of as components of a globally-defined function, 1-form and Riemannian metric on
transform as a function, 1-form and non-degenerate metric, respectively. Hence
they may be thought of as components of a globally-defined function, 1-form and Riemannian metric on
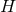 .
.
The coordinates developed above are valid in the neighbourhood of any smooth null hypersurface 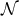 .
In this work we will in fact be concerned with smooth Killing horizons. These are null hypersurfaces that
possess a normal that is a Killing field
.
In this work we will in fact be concerned with smooth Killing horizons. These are null hypersurfaces that
possess a normal that is a Killing field 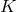 in
in 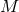 . Hence we may set
. Hence we may set 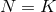 in the above construction.
Since
in the above construction.
Since 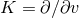 we deduce that in the neighbourhood of a Killing horizon
we deduce that in the neighbourhood of a Killing horizon 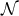 , the metric can be
written as Eq. (5
, the metric can be
written as Eq. (5 ) where the functions
) where the functions 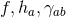 are all independent of the coordinate
are all independent of the coordinate  . Using the
Killing property one can rewrite
. Using the
Killing property one can rewrite 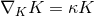 as
as 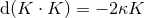 on
on 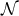 , where
, where  is now the usual
surface gravity of a Killing horizon.
is now the usual
surface gravity of a Killing horizon.
We may now introduce the main objects we will study in this work: degenerate Killing horizons. These
are defined as Killing horizons 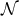 such that the normal Killing field
such that the normal Killing field 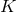 is tangent to affinely
parameterised null geodesics on
is tangent to affinely
parameterised null geodesics on 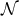 , i.e.,
, i.e., 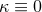 . Therefore,
. Therefore, 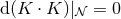 , which implies that in
Gaussian null coordinates
, which implies that in
Gaussian null coordinates 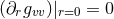 . It follows that
. It follows that 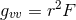 for some smooth function
for some smooth function 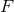 .
Therefore, in the neighbourhood of any smooth degenerate Killing horizon the metric in Gaussian null
coordinates reads
.
Therefore, in the neighbourhood of any smooth degenerate Killing horizon the metric in Gaussian null
coordinates reads
We are now ready to define the near-horizon geometry of a 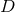 -dimensional spacetime
-dimensional spacetime 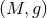 containing such a degenerate horizon. Given any
containing such a degenerate horizon. Given any 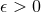 , consider the diffeomorphism defined by
, consider the diffeomorphism defined by 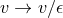 and
and 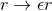 . The metric in Gaussian null coordinates transforms
. The metric in Gaussian null coordinates transforms 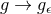 where
where 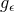 is given by Eq. (6
is given by Eq. (6 )
with the replacements
)
with the replacements 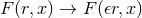 ,
, 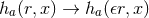 and
and 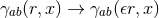 . The
near-horizon limit is then defined as the
. The
near-horizon limit is then defined as the 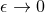 limit of
limit of 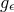 . It is clear this limit always exists since all
metric functions are smooth at
. It is clear this limit always exists since all
metric functions are smooth at 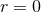 . The resulting metric is called the near-horizon geometry and is
given by
. The resulting metric is called the near-horizon geometry and is
given by
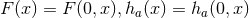 and
and 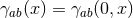 . Notice that the
. Notice that the  dependence of the
metric is completely fixed. In fact the near-horizon geometry is completely specified by the following
geometric data on the
dependence of the
metric is completely fixed. In fact the near-horizon geometry is completely specified by the following
geometric data on the 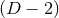 -dimensional cross section
-dimensional cross section 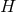 : a smooth function
: a smooth function 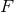 , 1-form
, 1-form 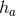 and
Riemannian metric
and
Riemannian metric 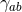 . We will often refer to the triple of data
. We will often refer to the triple of data 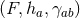 on
on 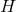 as the near-horizon
data.
as the near-horizon
data.
Intuitively, the near-horizon limit is a scaling limit that focuses on the spacetime near the horizon  .
We emphasise that the degenerate assumption
.
We emphasise that the degenerate assumption 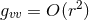 is crucial for defining this limit
and such a general notion of a near-horizon limit does not exist for a non-degenerate Killing
horizon.
is crucial for defining this limit
and such a general notion of a near-horizon limit does not exist for a non-degenerate Killing
horizon.
2.2 Curvature of near-horizon geometry
As we will see, geometric equations (such as Einstein’s equations) for a near-horizon geometry can be
equivalently written as geometric equations defined purely on a 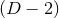 -dimensional cross section
manifold
-dimensional cross section
manifold 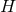 of the horizon. In this section we will write down general formulae relating the curvature of a
near-horizon geometry to the curvature of the horizon
of the horizon. In this section we will write down general formulae relating the curvature of a
near-horizon geometry to the curvature of the horizon 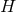 . For convenience we will denote the dimension of
. For convenience we will denote the dimension of
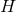 by
by 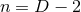 .
.
It is convenient to introduce a null-orthonormal frame for the near-horizon metric (7 ), denoted by
), denoted by
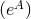 , where
, where 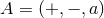 ,
, 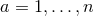 and
and
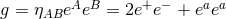 , where
, where 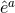 are vielbeins for the horizon metric
are vielbeins for the horizon metric
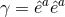 .10
The dual basis vectors are
where
.10
The dual basis vectors are
where 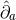 denote the dual vectors to
denote the dual vectors to 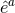 . The connection 1-forms satisfy
. The connection 1-forms satisfy 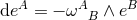 and are
given by
where
and are
given by
where 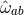 and
and  are the connection 1-forms and Levi-Civita connection of the metric
are the connection 1-forms and Levi-Civita connection of the metric 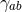 on
on
 respectively. The curvature two-forms defined by
respectively. The curvature two-forms defined by 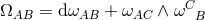 give the
Riemann tensor in this basis using
give the
Riemann tensor in this basis using 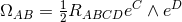 . The curvature two forms are:
where
. The curvature two forms are:
where 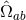 is the curvature of
is the curvature of 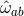 on
on 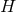 . The non-vanishing components of the Ricci tensor are thus
given by:
where
. The non-vanishing components of the Ricci tensor are thus
given by:
where 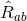 is the Ricci tensor of the metric
is the Ricci tensor of the metric 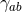 on
on 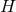 . The spacetime contracted Bianchi identity
implies the following identities on
. The spacetime contracted Bianchi identity
implies the following identities on 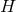 :
which may also be verified directly from the above expressions.
:
which may also be verified directly from the above expressions.
It is worth noting that the following components of the Weyl tensor automatically vanish:
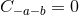 and
and 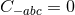 . This means that
. This means that 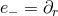 is a multiple Weyl aligned null direction
and hence any near-horizon geometry is at least algebraically special of type II within
the classification of [47]. In fact, it can be checked that the null geodesic vector field
is a multiple Weyl aligned null direction
and hence any near-horizon geometry is at least algebraically special of type II within
the classification of [47]. In fact, it can be checked that the null geodesic vector field 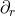 has
vanishing expansion, shear and twist and therefore any near-horizon geometry is a Kundt
spacetime.11
Indeed, by inspection of Eq. (7
has
vanishing expansion, shear and twist and therefore any near-horizon geometry is a Kundt
spacetime.11
Indeed, by inspection of Eq. (7 ) it is clear that near-horizon geometries are a subclass of the degenerate Kundt
spacetimes,12
which are all algebraically special of at least type II [184].
) it is clear that near-horizon geometries are a subclass of the degenerate Kundt
spacetimes,12
which are all algebraically special of at least type II [184].
Henceforth, we will drop the “hats” on all horizon quantities, so 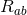 and
and 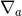 refer to the Ricci
tensor and Levi-Civita connection of
refer to the Ricci
tensor and Levi-Civita connection of 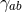 on
on 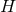 .
.
2.3 Einstein equations and energy conditions
We will consider spacetimes that are solutions to Einstein’s equations:
where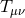 is the energy-momentum and
is the energy-momentum and 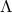 is the cosmological constant of our spacetime. We will be
interested in a variety of possible energy momentum tensors and thus in this section we will keep the
discussion general.
is the cosmological constant of our spacetime. We will be
interested in a variety of possible energy momentum tensors and thus in this section we will keep the
discussion general.
An important fact is that if a spacetime containing a degenerate horizon satisfies Einstein’s equations
then so does its near-horizon geometry. This is easy to see as follows. If the metric 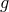 in Eq. (6
in Eq. (6 ) satisfies
Einstein’s equations, then so will the 1-parameter family of diffeomorphic metrics
) satisfies
Einstein’s equations, then so will the 1-parameter family of diffeomorphic metrics 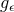 for any
for any 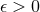 .
Hence the limiting metric
.
Hence the limiting metric 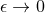 , which by definition is the near-horizon geometry, must also satisfy the
Einstein equations.
, which by definition is the near-horizon geometry, must also satisfy the
Einstein equations.
The near-horizon limit of the energy momentum tensor thus must also exist and takes the form
where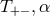 are functions on
are functions on 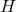 and
and 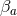 is a 1-form on
is a 1-form on 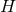 . Working in the vielbein frame
(8
. Working in the vielbein frame
(8 ), it is then straightforward to verify that the
), it is then straightforward to verify that the 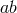 and
and 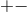 components of the Einstein
equations for the near-horizon geometry give the following equations on the cross section
components of the Einstein
equations for the near-horizon geometry give the following equations on the cross section 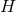 :
where we have defined
It may be shown that the rest of the Einstein equations are automatically satisfied as a consequence of
Eqs. (17
:
where we have defined
It may be shown that the rest of the Einstein equations are automatically satisfied as a consequence of
Eqs. (17 ), (18
), (18 ) and the matter field equations, as follows.
) and the matter field equations, as follows.
The matter field equations must imply the spacetime conservation equation 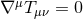 . This is
equivalent to the following equations on
. This is
equivalent to the following equations on 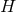 :
:
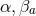 in terms of
in terms of 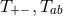 . The
. The
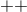 and
and 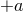 components of the Einstein equations are
components of the Einstein equations are 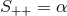 and
and 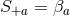 respectively, where
respectively, where
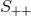 and
and 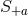 are defined in Eq. (12
are defined in Eq. (12 ). The first equation in (21
). The first equation in (21 ) and the identity (13
) and the identity (13 ) imply that the
) imply that the
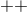 equation is satisfied as a consequence of the
equation is satisfied as a consequence of the 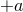 equation. Finally, substituting Eqs. (17
equation. Finally, substituting Eqs. (17 ) and
(18
) and
(18 ) into the identity (14
) into the identity (14 ), and using the second equation in (21
), and using the second equation in (21 ), implies the
), implies the 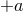 equation.
Alternatively, a tedious calculation shows that the
equation.
Alternatively, a tedious calculation shows that the 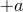 equation follows from Eqs. (17
equation follows from Eqs. (17 ) and
(18
) and
(18 ) using the contracted Bianchi identity for Eq. (17
) using the contracted Bianchi identity for Eq. (17 ), together with the second equation in
(21
), together with the second equation in
(21 ).
).
Although the energy momentum tensor must have a near-horizon limit, it is not obvious that the matter
fields themselves must. Thus, consider the full spacetime before taking the near-horizon limit. Recall that
for any Killing horizon  and therefore
and therefore 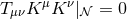 . This imposes a constraint on
the matter fields. We will illustrate this for Einstein–Maxwell theory whose energy-momentum tensor is
. This imposes a constraint on
the matter fields. We will illustrate this for Einstein–Maxwell theory whose energy-momentum tensor is
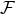 is the Maxwell 2-form, which must satisfy the Bianchi identity
is the Maxwell 2-form, which must satisfy the Bianchi identity 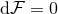 . It can be checked that
in Gaussian null coordinates
. It can be checked that
in Gaussian null coordinates 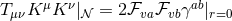 and hence we deduce that
and hence we deduce that 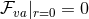 .
Thus, smoothness requires
.
Thus, smoothness requires 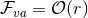 , which implies the near-horizon limit of
, which implies the near-horizon limit of 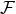 in fact exists.
Furthermore, imposing the Bianchi identity to the near-horizon limit of the Maxwell field relates
in fact exists.
Furthermore, imposing the Bianchi identity to the near-horizon limit of the Maxwell field relates 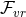 and
and
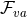 , allowing one to write
where
, allowing one to write
where 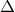 is a function on
is a function on 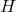 and
and 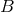 is a closed 2-form on
is a closed 2-form on 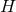 . The 2-form
. The 2-form 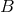 is the Maxwell field
induced on
is the Maxwell field
induced on 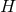 and locally can be written as
and locally can be written as 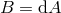 for some 1-form potential
for some 1-form potential 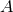 on
on 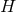 . It can be
checked that for the near-horizon limit
We will present the Maxwell equations in a variety of dimensions in Section 6.
. It can be
checked that for the near-horizon limit
We will present the Maxwell equations in a variety of dimensions in Section 6.
It is worth remarking that the above naturally generalises to 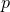 -form electrodynamics, with
-form electrodynamics, with 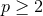 ,
for which the energy momentum tensor is
,
for which the energy momentum tensor is
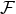 is a
is a 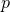 -form field strength satisfying the Bianchi identity
-form field strength satisfying the Bianchi identity 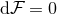 . It is then easily checked
that
. It is then easily checked
that 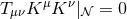 implies
implies 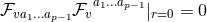 and hence
and hence 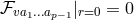 . Thus,
smoothness requires
. Thus,
smoothness requires 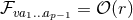 , which implies that the near-horizon limit of the
, which implies that the near-horizon limit of the 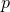 -form
exists. The Bianchi identity then implies that the most general form for the near-horizon limit is
where
-form
exists. The Bianchi identity then implies that the most general form for the near-horizon limit is
where 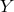 is a
is a  -form on
-form on 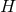 and
and 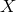 is a closed
is a closed 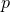 -form on
-form on 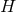 .
.
The Einstein equations for a near-horizon geometry can also be interpreted as geometrical equations
arising from the restriction of the Einstein equations for the full spacetime to a degenerate horizon, without
taking the near-horizon limit, as follows. The near-horizon limit can be thought of as the 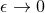 limit of
the “boost” transformation
limit of
the “boost” transformation 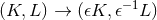 . This implies that restricting the boost-invariant
components of the Einstein equations for the full spacetime to a degenerate horizon is equivalent to the
boost invariant components of the Einstein equations for the near-horizon geometry. The boost-invariant
components are
. This implies that restricting the boost-invariant
components of the Einstein equations for the full spacetime to a degenerate horizon is equivalent to the
boost invariant components of the Einstein equations for the near-horizon geometry. The boost-invariant
components are 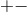 and
and 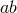 and hence we see that Eqs. (17
and hence we see that Eqs. (17 ) and (18
) and (18 ) are also valid for the full
spacetime quantities restricted to the horizon. We deduce that the restriction of these components of the
Einstein equations depends only on data intrinsic to
) are also valid for the full
spacetime quantities restricted to the horizon. We deduce that the restriction of these components of the
Einstein equations depends only on data intrinsic to 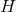 : this special feature only arises for degenerate
horizons.13
It is worth noting that the horizon equations (17
: this special feature only arises for degenerate
horizons.13
It is worth noting that the horizon equations (17 ) and (18
) and (18 ) remain valid in the more general context of
extremal isolated horizons [163
) remain valid in the more general context of
extremal isolated horizons [163 , 209, 28] and Kundt metrics [144
, 209, 28] and Kundt metrics [144 ].
].
The positivity of 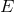 and
and 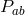 can be related to standard energy conditions. For a near-horizon
geometry
can be related to standard energy conditions. For a near-horizon
geometry 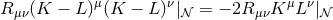 . Since
. Since  is timelike on the horizon, the
strong energy condition implies
is timelike on the horizon, the
strong energy condition implies 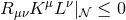 . Hence, noting that
. Hence, noting that 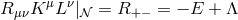 we
deduce that the strong energy condition implies
we
deduce that the strong energy condition implies
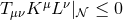 . One can show
. One can show
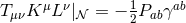 . Therefore, the dominant energy condition implies
Since
. Therefore, the dominant energy condition implies
Since  , if
, if 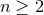 the dominant energy condition implies
the dominant energy condition implies 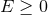 : hence, if
: hence, if 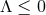 the
dominant energy condition implies both Eqs. (28
the
dominant energy condition implies both Eqs. (28 ) and (29
) and (29 ). Observe that Einstein–Maxwell theory with
). Observe that Einstein–Maxwell theory with
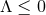 satisfies both of these conditions.
satisfies both of these conditions.
In this review, we describe the current understanding of the space of solutions to the basic horizon
equation (17 ), together with the appropriate horizon matter field equations, in a variety of dimensions and
theories.
), together with the appropriate horizon matter field equations, in a variety of dimensions and
theories.
2.4 Physical charges
So far we have considered near-horizon geometries independently of any extremal–black-hole solutions. In
this section we will assume that the near-horizon geometry arises from a near-horizon limit of an extremal
black hole. This limit discards the asymptotic data of the parent–black-hole solution. As a result, only a
subset of the physical properties of a black hole can be calculated from the near-horizon geometry alone. In
particular, information about the asymptotic stationary Killing vector field is lost and hence one cannot
compute the mass from a Komar integral, nor can one compute the angular velocity of the horizon with
respect to infinity. Below we discuss physical properties that can be computed purely from the near-horizon
geometry [123 , 79
, 79 , 154
, 154 ].
].
Area. The area of cross sections of the horizon 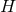 is defined by
is defined by
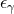 is the volume form associated to the induced Riemannian metric
is the volume form associated to the induced Riemannian metric 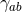 on
on 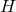 .
.
For definiteness we now assume the parent black hole is asymptotically flat.
Angular momentum. The conserved angular momentum associated with a rotational symmetry,
generated by a Killing vector 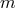 , is given by a Komar integral on a sphere at spacelike infinity
, is given by a Komar integral on a sphere at spacelike infinity
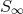 :14
:14
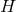 , by applying Stokes’
theorem to a spacelike hypersurface
, by applying Stokes’
theorem to a spacelike hypersurface 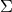 with boundary
with boundary 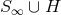 . The field equations can be used to
evaluate the volume integral that is of the form
. The field equations can be used to
evaluate the volume integral that is of the form 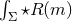 , where
, where 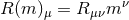 . In particular, for
vacuum gravity one simply has:
For Einstein–Maxwell theories the integral
. In particular, for
vacuum gravity one simply has:
For Einstein–Maxwell theories the integral 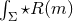 can also be written as an integral over
can also be written as an integral over 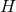 , giving
extra terms that correspond to the contribution of the matter fields to the angular momentum. For
example, consider pure Einstein–Maxwell theory in any dimension so the Maxwell equation is
, giving
extra terms that correspond to the contribution of the matter fields to the angular momentum. For
example, consider pure Einstein–Maxwell theory in any dimension so the Maxwell equation is 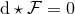 .
Parameterising the near-horizon Maxwell field by (23
.
Parameterising the near-horizon Maxwell field by (23 ) one can show that, in the gauge
) one can show that, in the gauge 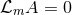 ,
so the angular momentum is indeed determined by the near-horizon data.
,
so the angular momentum is indeed determined by the near-horizon data.
In five spacetime dimensions it is natural to couple Einstein–Maxwell theory to a Chern–Simons (CS) term. While the Einstein equations are unchanged, the Maxwell equation now becomes
where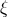 is the CS coupling constant. The angular momentum in this case can also be written purely as an
integral over
is the CS coupling constant. The angular momentum in this case can also be written purely as an
integral over 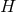 :
Of particular interest is the theory defined by CS coupling
:
Of particular interest is the theory defined by CS coupling 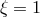 , since this corresponds to the bosonic
sector of minimal supergravity.
, since this corresponds to the bosonic
sector of minimal supergravity.
Gauge charges. For Einstein–Maxwell theories there are also electric, and possibly magnetic, charges. For example, in pure Einstein–Maxwell theory in any dimension, the electric charge is written as an integral over spatial infinity:
By applying Stokes’ Theorem to a spacelike hypersurface as above, and using the Maxwell equation,
one easily finds
For
as above, and using the Maxwell equation,
one easily finds
For  Einstein–Maxwell–CS theory one instead gets
For
Einstein–Maxwell–CS theory one instead gets
For  one also has a conserved magnetic charge
one also has a conserved magnetic charge  . Using the Bianchi identity this
can be written as
For
. Using the Bianchi identity this
can be written as
For 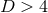 asymptotically-flat black holes there is no conserved magnetic charge. However, for
asymptotically-flat black holes there is no conserved magnetic charge. However, for
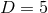 black rings
black rings 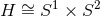 , one can define a quasi-local dipole charge over the
, one can define a quasi-local dipole charge over the 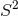 where in the second equality we have expressed it in terms of the horizon Maxwell field.
where in the second equality we have expressed it in terms of the horizon Maxwell field.
Note that in general the gauge field 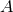 will not be globally defined on
will not be globally defined on 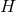 , so care must be taken to
evaluate expressions such as (35
, so care must be taken to
evaluate expressions such as (35 ) and (38
) and (38 ), see [123, 155
), see [123, 155 ].
].

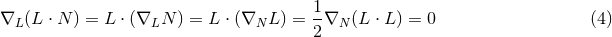
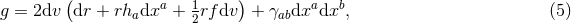
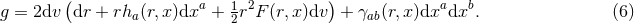
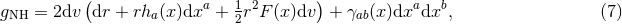
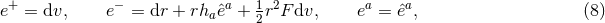
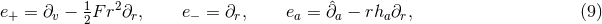
![ω+− = rF e+ + 1haea, ω+a = 1r2(∂ˆaF − F ha)e+ − 1hae − + rˆ∇ [ahb]eb, 1 + 2 2 + 2 ω −a = − 2hae , ωab = ˆωab − r ˆ∇[ahb]e , (10 )](article191x.gif)
![( ) Ω = Ωˆ + e+ ∧ e− ˆ∇ h + re+ ∧ ed − h ˆ∇ h + ˆ∇ ∇ˆ h + 1h ˆ∇ h − 1h ∇ˆ h , ab ab [a b] ( d [a b] d [a b] )2 a [b d] 2 b [a d] (1- ) + − b + ˆ 1 ˆ 1ˆ a b Ω+ − = 4haha − F e ∧ e + re ∧ e ∂bF − F hb + 2ha∇ [ahb] + 2∇ [ahb]e ∧ e , 2 + d [( 1ˆ ) ˆ 1 ˆ ˆ ˆ 1 ˆ ] Ω+a = r e ∧ e − 2∇d + hd (∂aF − F ha) + 2F ∇ [ahd] + ∇[cha]∇ [chd] + 2h [a∇d ]F + − ( 1 ) 1 − b( 1 ) + re ∧ e haF − ∂ˆaF − 2hb∇ˆ[bha ] + 2 e ∧ e ˆ∇ahb − 2hahb ( ) + reb ∧ ed − ∇ˆd ˆ∇ [ahb] + 12ha∇ˆ[dhb] − 12hb∇ˆ[ahd ] , ( ) Ω−a = 12e+ ∧ eb ∇ˆbha − 12hahb , (11 )](article198x.gif)
![R+ − = F − 12haha + 12 ˆ∇aha, ˆ ˆ 1 Rab = Rab[ + ∇ (ahb) − 2hahb, ] R = r2 − 1ˆ∇2F + 3haˆ∇ F + 1F∇ˆah − F h h + ∇ˆ h ˆ∇ h ≡ r2S , ++ [ 2 2 a 2 a ]a a [c a] [c a] ++ R = r ∇ˆ F − Fh − 2h ˆ∇ h + ∇ˆ ˆ∇ h ≡ rS , (12 ) +a a a b [a b] b [a b] +a](article202x.gif)
![S++ = − 12(∇ˆa − 2ha)S+a, (13 ) ˆ b 1 c b S+a = − ∇ [Rba − 2γba(R c + 2R+ − )] + h Rba − haR+ − , (14 )](article207x.gif)