3 General Results
In this section we describe a number of general results concerning the topology and symmetry of near-horizon geometries under various assumptions.
3.1 Horizon topology theorem
Hawking’s horizon topology theorem is one of the fundamental ingredients of the classic four-dimensional
black-hole uniqueness theorems [127 ]. It states that cross sections of the event horizon of an
asymptotically-flat, stationary, black-hole solution to Einstein’s equations, satisfying the dominant
energy condition, must be homeomorphic to
]. It states that cross sections of the event horizon of an
asymptotically-flat, stationary, black-hole solution to Einstein’s equations, satisfying the dominant
energy condition, must be homeomorphic to 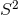 . The proof is an elegant variational argument
that shows that any cross section with negative Euler characteristic can be deformed outside
the event horizon such that its outward null geodesics converge. This means one has an outer
trapped surface outside the event horizon, which is not allowed by general results on black
holes.15
. The proof is an elegant variational argument
that shows that any cross section with negative Euler characteristic can be deformed outside
the event horizon such that its outward null geodesics converge. This means one has an outer
trapped surface outside the event horizon, which is not allowed by general results on black
holes.15
Galloway and Schoen have shown how to generalise Hawking’s horizon topology theorem to higher
dimensional spacetimes [91 ]. Their theorem states if the dominant energy condition holds, a cross section
]. Their theorem states if the dominant energy condition holds, a cross section 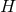 of the horizon of a black hole, or more generally a marginally outer trapped surface, must have positive Yamabe
invariant.16
The positivity of the Yamabe invariant, which we define below, is equivalent to the existence of a
positive scalar curvature metric and is well known to impose restrictions on the topology, see, e.g.,
[89]. For example, when
of the horizon of a black hole, or more generally a marginally outer trapped surface, must have positive Yamabe
invariant.16
The positivity of the Yamabe invariant, which we define below, is equivalent to the existence of a
positive scalar curvature metric and is well known to impose restrictions on the topology, see, e.g.,
[89]. For example, when 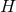 is three dimensional, the only possibilities are connected sums of
is three dimensional, the only possibilities are connected sums of
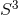 (and their quotients) and
(and their quotients) and 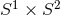 , consistent with the known examples of black-hole
solutions.
, consistent with the known examples of black-hole
solutions.
In the special case of degenerate horizons a simple proof of this topology theorem can be given directly
from the near-horizon geometry [166 ]. This is essentially a specialisation of the simplified proof of the
Galloway–Schoen theorem given in [189
]. This is essentially a specialisation of the simplified proof of the
Galloway–Schoen theorem given in [189 ]. However, we note that since we only use properties of the
near-horizon geometry, in particular only the horizon equation (17
]. However, we note that since we only use properties of the
near-horizon geometry, in particular only the horizon equation (17 ), we do not require the existence of a
black hole.
), we do not require the existence of a
black hole.
For four dimensional spacetimes, so dim 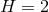 , the proof is immediate, see, e.g., [144, 152
, the proof is immediate, see, e.g., [144, 152 ].
].
Theorem 3.1. Consider a spacetime containing a degenerate horizon with a compact cross section
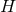 and assume the dominant energy condition holds. If
and assume the dominant energy condition holds. If 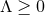 then
then 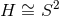 , except for the
special case where the near-horizon geometry is flat (so
, except for the
special case where the near-horizon geometry is flat (so 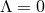 ) and
) and 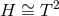 . If
. If 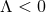 and
and
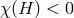 the area of
the area of 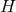 satisfies
satisfies 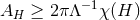 with equality if and only if the near-horizon
geometry is
with equality if and only if the near-horizon
geometry is 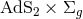 , where
, where 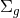 is a compact quotient of hyperbolic space of genus
is a compact quotient of hyperbolic space of genus 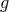 .
.
The proof is elementary. The Euler characteristic of 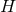 can be calculated by integrating the trace of
Eq. (17
can be calculated by integrating the trace of
Eq. (17 ) over
) over 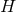 to get
to get
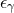 is the volume form of the horizon metric
is the volume form of the horizon metric 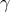 . Therefore, for
. Therefore, for 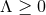 and matter satisfying the
dominant energy condition
and matter satisfying the
dominant energy condition 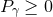 (see Eq. (29
(see Eq. (29 )), it follows that
)), it follows that 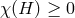 . Equality can only occur if
. Equality can only occur if
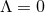 ,
, 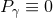 ,
, 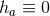 : using Eqs. (17
: using Eqs. (17 ) and (18
) and (18 ) this implies
) this implies 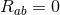 and
and 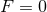 , so the
near-horizon geometry is the trivial flat solution
, so the
near-horizon geometry is the trivial flat solution 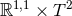 . For the
. For the 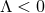 case the above argument fails
and one finds no restriction on the topology of
case the above argument fails
and one finds no restriction on the topology of 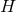 . Instead, for
. Instead, for 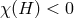 , one can derive a lower bound
for the area of
, one can derive a lower bound
for the area of 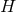 :
This agrees with the lower bounds found in [95, 208] in the more general context of apparent horizons. The
lower bound in Eq. (42
:
This agrees with the lower bounds found in [95, 208] in the more general context of apparent horizons. The
lower bound in Eq. (42 ) is saturated if and only if
) is saturated if and only if 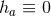 ,
, 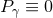 , which implies
, which implies 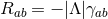 and
and
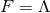 , so the near-horizon geometry is
, so the near-horizon geometry is 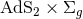 .
.
It is of interest to generalise these results to higher dimensions along the lines of Galloway and Schoen.
As is well known, the total integral of the scalar curvature in itself does not constrain the topology of
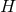 in this case. An analogue of this invariant for dim
in this case. An analogue of this invariant for dim 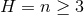 is given by the Yamabe
invariant
is given by the Yamabe
invariant 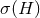 . This is defined via the Yamabe constant associated to a given conformal
class of metrics
. This is defined via the Yamabe constant associated to a given conformal
class of metrics ![[γ]](article399x.gif) on
on 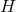 . First consider the volume-normalised Einstein–Hilbert functional
. First consider the volume-normalised Einstein–Hilbert functional
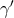 is a Riemannian metric on
is a Riemannian metric on 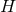 and
and 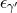 is the associated volume form. As is well known, this
functional is neither bounded from above or below. However, the restriction of
is the associated volume form. As is well known, this
functional is neither bounded from above or below. However, the restriction of 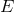 to any conformal class
of metrics is always bounded from below: the Yamabe constant
to any conformal class
of metrics is always bounded from below: the Yamabe constant ![Y (H, [γ ])](article406x.gif) for a given conformal
class is then defined as the infimum of this functional. Parameterising the conformal class by
for a given conformal
class is then defined as the infimum of this functional. Parameterising the conformal class by
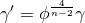 , for smooth positive functions
, for smooth positive functions 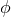 , we have
, we have ![Y(H, [γ]) ≡ infϕ>0 E γ[ϕ]](article409x.gif) , where
The Yamabe invariant
, where
The Yamabe invariant 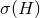 is defined by
is defined by ![σ(H ) = sup Y(H, [γ]) [γ]](article412x.gif) , where the supremum is taken over
all possible conformal classes. The solution to the Yamabe problem states the following remarkable fact: for
every conformal class
, where the supremum is taken over
all possible conformal classes. The solution to the Yamabe problem states the following remarkable fact: for
every conformal class ![[γ ]](article413x.gif) on compact
on compact 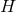 , the functional
, the functional ![E γ[ϕ ]](article415x.gif) achieves its infimum and this occurs for
a constant scalar curvature metric.
achieves its infimum and this occurs for
a constant scalar curvature metric.
We are now ready to present the degenerate horizon topology theorem.
Theorem 3.2. Consider a spacetime containing a degenerate horizon with a compact cross section 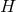 and assume the dominant energy condition holds. If
and assume the dominant energy condition holds. If 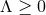 , then either
, then either 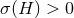 or the
induced metric on the horizon is Ricci flat. If
or the
induced metric on the horizon is Ricci flat. If 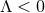 and
and 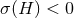 the area of
the area of 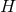 satisfies
satisfies
A simple proof exploits the solution to the Yamabe problem mentioned above [189, 166 ]. First
observe that if there exists a conformal class of metrics
]. First
observe that if there exists a conformal class of metrics ![[γ]](article423x.gif) for which the Yamabe constant
for which the Yamabe constant
![Y (H, [γ ]) > 0](article424x.gif) then it follows that
then it follows that 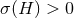 . Therefore, to establish that
. Therefore, to establish that 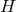 has positive Yamabe
invariant, it is sufficient to show that for some
has positive Yamabe
invariant, it is sufficient to show that for some 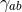 the functional
the functional ![E [ϕ] > 0 γ](article428x.gif) for all
for all 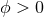 ,
since the solution to the Yamabe problem then tells us that
,
since the solution to the Yamabe problem then tells us that ![Y (H,[γ]) = E γ[ϕ0] > 0](article430x.gif) for some
for some
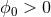 .
.
For our Riemannian manifolds 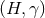 it is easy to show, except for one exceptional circumstance, that
it is easy to show, except for one exceptional circumstance, that
![E γ[ϕ] > 0](article433x.gif) for all
for all 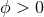 and thus
and thus ![Y(H, [γ]) > 0](article435x.gif) . The proof is as follows. The horizon equation (17
. The proof is as follows. The horizon equation (17 )
can be used to establish the identity
)
can be used to establish the identity
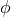 , where we have defined the differential operator
, where we have defined the differential operator 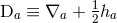 . It is worth noting that this
identity relies crucially on the precise constants appearing in Eq. (17
. It is worth noting that this
identity relies crucially on the precise constants appearing in Eq. (17 ). This implies the following integral
identity over
). This implies the following integral
identity over  :
If
:
If 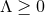 , the dominant energy condition
, the dominant energy condition 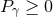 implies
implies ![Eγ[ϕ] ≥ 0](article443x.gif) for all
for all 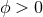 with equality only
if
with equality only
if 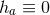 ,
, 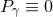 and
and 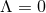 . The exceptional case
. The exceptional case 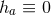 ,
, 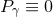 and
and 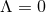 implies
implies 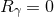 ,
which allows one to infer [91] that either
,
which allows one to infer [91] that either 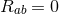 or
or 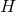 admits a metric of positive scalar curvature
(and is thus positive Yamabe after all).
admits a metric of positive scalar curvature
(and is thus positive Yamabe after all).
As in four spacetime dimensions the above argument fails for 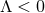 , and thus provides no restriction
of the topology of
, and thus provides no restriction
of the topology of 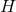 . Instead, assuming the dominant energy condition, Eq. (47
. Instead, assuming the dominant energy condition, Eq. (47 ) implies
) implies
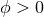 , where the second inequality follows from Hölder’s inequality. Therefore, by the definition
of
, where the second inequality follows from Hölder’s inequality. Therefore, by the definition
of ![Y (H, [γ])](article458x.gif) , we deduce that
, we deduce that ![2∕n Y (H,[γ]) ≥ − n|Λ|AH](article459x.gif) . It follows that if
. It follows that if 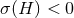 , we get the stated
non-trivial lower bound on the area of
, we get the stated
non-trivial lower bound on the area of 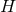 . We note that the lower bound can only be achieved if
. We note that the lower bound can only be achieved if 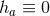 and
and 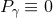 , which implies
, which implies 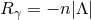 , in which case
, in which case 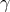 necessarily minimises the functional
necessarily minimises the functional 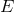 in
the conformal class
in
the conformal class ![[γ ]](article467x.gif) so that
so that ![Y(H, [γ]) = − n |Λ |A2∕n H](article468x.gif) . However, since
. However, since ![− Y (H, [γ]) ≥ |σ(H )|](article469x.gif) , it need
not be the case that the lower bound in Eq. (45
, it need
not be the case that the lower bound in Eq. (45 ) is saturated by such horizon metrics (in contrast to the
) is saturated by such horizon metrics (in contrast to the
 case above).
case above).
We note that the above topology theorems in fact only employ the scalar curvature of the horizon metric
and not the full horizon equation (17 ). It would be interesting if one could use the non-trace part of the
horizon equation to derive further topological restrictions.
). It would be interesting if one could use the non-trace part of the
horizon equation to derive further topological restrictions.
3.2 AdS2-structure theorems
It is clear that a general near-horizon geometry, Eq. (7 ), possesses enhanced symmetry: in addition to
the translation symmetry
), possesses enhanced symmetry: in addition to
the translation symmetry 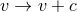 one also has a dilation symmetry
one also has a dilation symmetry 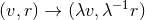 where
where 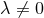 and together these form a two-dimensional non-Abelian isometry group. In this
section we will discuss various near-horizon symmetry theorems that guarantee further enhanced
symmetry.
and together these form a two-dimensional non-Abelian isometry group. In this
section we will discuss various near-horizon symmetry theorems that guarantee further enhanced
symmetry.
3.2.1 Static near-horizon geometries
A static near-horizon geometry is one for which the normal Killing field  is hypersurface orthogonal,
i.e.,
is hypersurface orthogonal,
i.e., 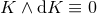 everywhere.
everywhere.
Theorem 3.3 ([162 ]). Any static near-horizon geometry is locally a warped product of AdS2, dS2 or
]). Any static near-horizon geometry is locally a warped product of AdS2, dS2 or
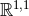 and
and 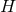 . If
. If 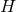 is simply connected this statement is global. In this case if
is simply connected this statement is global. In this case if 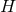 is compact
and the strong energy conditions holds it must be the AdS2 case or the direct product
is compact
and the strong energy conditions holds it must be the AdS2 case or the direct product 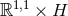 .
.
Proof : As a 1-form 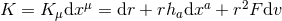 . A short calculation then reveals that
. A short calculation then reveals that
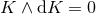 if and only if
if and only if
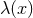 is a function on
is a function on 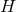 and
and 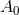 is a constant. Substituting these into the near-horizon
geometry and changing the affine parameter
is a constant. Substituting these into the near-horizon
geometry and changing the affine parameter 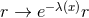 gives:
The metric in the square bracket is a maximally symmetric space: AdS2 for
gives:
The metric in the square bracket is a maximally symmetric space: AdS2 for 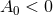 , dS2 for
, dS2 for 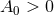 and
and
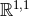 for
for 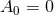 . If
. If 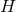 is simply connected then
is simply connected then 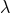 is globally defined on
is globally defined on 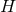 . Now consider
Eq. (18
. Now consider
Eq. (18 ), which in this case reduces to
Assume
), which in this case reduces to
Assume 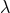 is a globally-defined function. Integrating over
is a globally-defined function. Integrating over 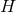 shows that if the strong energy
condition (28
shows that if the strong energy
condition (28 ) holds then
) holds then 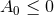 . The equality
. The equality 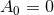 occurs if and only if
occurs if and only if 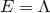 , in which case
, in which case
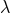 is harmonic and hence a constant.
is harmonic and hence a constant.
3.2.2 Near-horizon geometries with rotational symmetries
We begin by considering near-horizon geometries with a 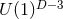 rotational symmetry, whose orbits are
generically cohomogeneity-1 on cross sections of the horizon
rotational symmetry, whose orbits are
generically cohomogeneity-1 on cross sections of the horizon 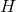 . The orbit spaces
. The orbit spaces 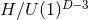 have been
classified and are homeomorphic to either the closed interval or a circle, see, e.g., [139
have been
classified and are homeomorphic to either the closed interval or a circle, see, e.g., [139 ]. The former
corresponds to
]. The former
corresponds to 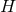 of topology
of topology 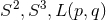 times an appropriate dimensional torus, whereas
the latter corresponds to
times an appropriate dimensional torus, whereas
the latter corresponds to 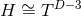 . Unless otherwise stated we will assume non-toroidal
topology.
. Unless otherwise stated we will assume non-toroidal
topology.
It turns out to be convenient to work with a geometrically-defined set of coordinates as introduced
in [152 ]. Let
]. Let 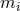 for
for 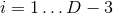 be the Killing vector fields generating the isometry. Define the
1-form
be the Killing vector fields generating the isometry. Define the
1-form 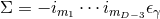 , where
, where 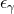 is the volume form associated with the metric
is the volume form associated with the metric 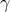 on
on 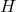 . Note
that
. Note
that 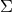 is closed and invariant under the Killing fields
is closed and invariant under the Killing fields 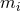 and so defines a closed one-form on
the orbit space. Hence there exists a globally-defined invariant function
and so defines a closed one-form on
the orbit space. Hence there exists a globally-defined invariant function 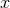 on
on 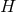 such that
such that
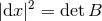 , where
, where 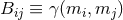 , so
, so 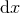 vanishes precisely at the endpoints of the
closed interval where the matrix
vanishes precisely at the endpoints of the
closed interval where the matrix 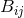 has rank
has rank  . As a function on
. As a function on 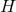 ,
, 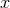 has precisely one
minimum
has precisely one
minimum 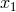 and one maximum
and one maximum 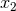 , which must occur at the endpoints of the orbit space. Hence
, which must occur at the endpoints of the orbit space. Hence
![D− 3 ∼ H ∕U (1) = [x1,x2]](article530x.gif) .
.
Introducing coordinates adapted to the Killing fields 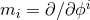 , we can use
, we can use 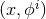 as a chart on
as a chart on
 everywhere except the endpoints of the orbit space. The metric for
everywhere except the endpoints of the orbit space. The metric for 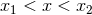 then reads
then reads
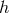 may be decomposed globally on
may be decomposed globally on 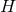 as
where
as
where 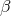 is co-closed. Since
is co-closed. Since  is invariant under the
is invariant under the 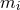 , it follows that
, it follows that 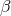 and
and 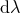 are as well.
Further, periodicity of the orbits of the
are as well.
Further, periodicity of the orbits of the 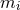 implies
implies 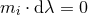 , i.e.,
, i.e., 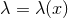 . It is convenient to
define the globally-defined positive function
Next, writing
. It is convenient to
define the globally-defined positive function
Next, writing 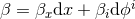 and imposing that
and imposing that 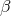 is co-closed, implies
is co-closed, implies 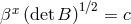 , where
, where
 is a constant. It follows
is a constant. It follows 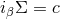 and since
and since 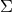 vanishes at the fixed points of the
vanishes at the fixed points of the 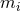 , this implies
, this implies
 must vanish. Hence we may write
where we define
must vanish. Hence we may write
where we define 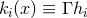 . It is worth noting that in the toroidal case one can introduce coordinates
. It is worth noting that in the toroidal case one can introduce coordinates
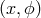 so that the horizon metric takes the same form, with
so that the horizon metric takes the same form, with 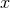 now periodic and
now periodic and 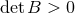 everywhere, although now the one-form
everywhere, although now the one-form 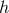 may have an extra term since the constant
may have an extra term since the constant  need not
vanish [131
need not
vanish [131 ].
].
We are now ready to state the simplest of the AdS2 near-horizon symmetry enhancement theorems:
Theorem 3.4 ([162 ]). Consider a
]). Consider a 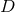 -dimensional spacetime containing a degenerate horizon,
invariant under an
-dimensional spacetime containing a degenerate horizon,
invariant under an 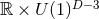 isometry group, and satisfying the Einstein equations
isometry group, and satisfying the Einstein equations
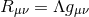 . Then the near-horizon geometry has a global
. Then the near-horizon geometry has a global 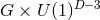 symmetry, where
symmetry, where 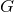 is
either
is
either 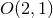 or the 2D Poincaré group. Furthermore, if
or the 2D Poincaré group. Furthermore, if 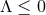 and the near-horizon geometry
is non-static the Poincaré case is excluded.
and the near-horizon geometry
is non-static the Poincaré case is excluded.
Proof: For the non-toroidal case we use the above coordinates. By examining the 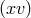 and
and 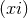 components of the spacetime Einstein equations and changing the affine parameter
components of the spacetime Einstein equations and changing the affine parameter 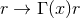 , one can
show
, one can
show
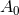 and
and 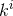 are constants. The metric in the square bracket is a maximally-symmetric space:
AdS2 for
are constants. The metric in the square bracket is a maximally-symmetric space:
AdS2 for 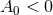 , dS2 for
, dS2 for 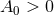 and
and 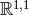 for
for 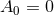 . Any isometry of these 2D base
spaces transforms
. Any isometry of these 2D base
spaces transforms 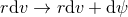 , for some function
, for some function 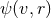 . Therefore, by simultaneously
transforming
. Therefore, by simultaneously
transforming 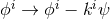 , the full near-horizon geometry inherits the full isometry group
, the full near-horizon geometry inherits the full isometry group
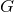 of the 2D base, which for
of the 2D base, which for 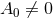 is
is 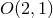 and for
and for 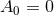 is the 2D Poincaré
group.
is the 2D Poincaré
group.
The toroidal case can in fact be excluded [131 ], although as remarked above the coordinate system
needs to be developed differently.
], although as remarked above the coordinate system
needs to be developed differently.
In fact as we will see in Section 4 one can completely solve for the near-horizon geometries of the above
form in the 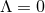 case.
case.
The above result has a natural generalisation for 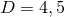 Einstein–Maxwell theories. For the sake of
generality, consider a general 2-derivative theory describing Einstein gravity coupled to Abelian vectors
Einstein–Maxwell theories. For the sake of
generality, consider a general 2-derivative theory describing Einstein gravity coupled to Abelian vectors
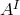 (
(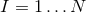 ) and uncharged scalars
) and uncharged scalars 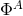 (
(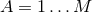 ) in
) in 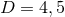 dimensions, with action
dimensions, with action
 ,
, 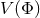 is an arbitrary scalar potential (which allows for a cosmological constant), and
or
where
is an arbitrary scalar potential (which allows for a cosmological constant), and
or
where 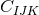 are constants. This encompasses many theories of interest, e.g., vacuum gravity with a
cosmological constant, Einstein–Maxwell theory, and various (possibly gauged) supergravity theories arising
from compactification from ten or eleven dimensions.
are constants. This encompasses many theories of interest, e.g., vacuum gravity with a
cosmological constant, Einstein–Maxwell theory, and various (possibly gauged) supergravity theories arising
from compactification from ten or eleven dimensions.
Theorem 3.5 ([162 ]). Consider an extremal–black-hole solution of the above
]). Consider an extremal–black-hole solution of the above 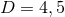 theory
with
theory
with 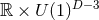 symmetry. The near-horizon limit of this solution has a global
symmetry. The near-horizon limit of this solution has a global 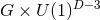 symmetry, where
symmetry, where 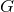 is either
is either 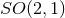 or (the orientation-preserving subgroup of) the 2D
Poincaré group. The Poincaré-symmetric case is excluded if
or (the orientation-preserving subgroup of) the 2D
Poincaré group. The Poincaré-symmetric case is excluded if 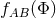 and
and 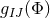 are positive
definite, the scalar potential is non-positive, and the horizon topology is not
are positive
definite, the scalar potential is non-positive, and the horizon topology is not 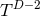 .
.
Proof: The Maxwell fields 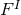 and the scalar fields are invariant under the Killing fields
and the scalar fields are invariant under the Killing fields 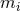 , hence
, hence
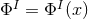 . By examining the
. By examining the 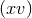 and
and 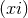 components of Einstein’s equations for the above
general theory, and changing the affine parameter
components of Einstein’s equations for the above
general theory, and changing the affine parameter 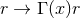 , one can show that the near-horizon metric
is given by Eq. (58
, one can show that the near-horizon metric
is given by Eq. (58 ) and the Maxwell fields are given by
) and the Maxwell fields are given by
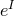 are constants. Hence both the near-horizon metric and Maxwell fields are invariant under
are constants. Hence both the near-horizon metric and Maxwell fields are invariant under
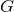 . Generic orbits of the symmetry group have the structure of
. Generic orbits of the symmetry group have the structure of 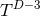 fibred over a 2D
maximally-symmetric space, i.e., AdS2, dS2 or
fibred over a 2D
maximally-symmetric space, i.e., AdS2, dS2 or 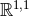 . AdS
2 and dS2 give
. AdS
2 and dS2 give 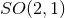 symmetry,
whereas
symmetry,
whereas 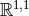 gives Poincaré symmetry. The dS
2 and
gives Poincaré symmetry. The dS
2 and 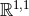 cases are excluded subject to
the additional assumptions mentioned, which ensure that the theory obeys the strong energy
condition.
cases are excluded subject to
the additional assumptions mentioned, which ensure that the theory obeys the strong energy
condition.
Remarks:
- In the original statement of this theorem asymptotically-flat or AdS boundary conditions were
assumed [162
 ]. These were only used at one point in the proof, where the property that the
generator of each rotational symmetry must vanish somewhere in the asymptotic region (on the
“axis” of the symmetry) was used to constrain the Maxwell fields. In fact, using the general form
for the near-horizon limit of a Maxwell field (23
]. These were only used at one point in the proof, where the property that the
generator of each rotational symmetry must vanish somewhere in the asymptotic region (on the
“axis” of the symmetry) was used to constrain the Maxwell fields. In fact, using the general form
for the near-horizon limit of a Maxwell field (23 ) and the fact that for non-toroidal topology
at least one of the rotational Killing fields must vanish somewhere, allows one to remove any
assumptions on the asymptotics of the black-hole spacetime.
) and the fact that for non-toroidal topology
at least one of the rotational Killing fields must vanish somewhere, allows one to remove any
assumptions on the asymptotics of the black-hole spacetime.
- In the context of black holes, toroidal topology is excluded for
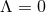 when the dominant
energy condition holds by the black-hole–topology theorems.
when the dominant
energy condition holds by the black-hole–topology theorems.
An important corollary of the above theorems is:
Corollary 3.1. Consider a 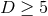 spacetime with a degenerate horizon invariant under a
spacetime with a degenerate horizon invariant under a
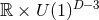 symmetry as in Theorem 3.4 and 3.5. The near-horizon geometry is static if it
is either a warped product of AdS2 and
symmetry as in Theorem 3.4 and 3.5. The near-horizon geometry is static if it
is either a warped product of AdS2 and 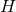 , or it is a warped product of locally AdS3 and a
, or it is a warped product of locally AdS3 and a
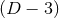 -manifold.
-manifold.
The static conditions (49 ) for Eq. (58
) for Eq. (58 ) occur if and only if: (i)
) occur if and only if: (i) 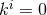 for all
for all 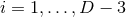 , or (ii)
, or (ii)
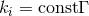 and
and 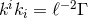 with
with 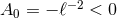 . Case (i) gives a warped product of a 2D
maximally-symmetric space and
. Case (i) gives a warped product of a 2D
maximally-symmetric space and 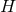 as in Theorem (3.3). For case (ii) one can introduce
as in Theorem (3.3). For case (ii) one can introduce 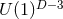 coordinates
coordinates 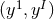 where
where 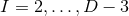 , not necessarily periodic, so that
, not necessarily periodic, so that 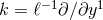 and
and
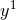 is a periodic coordinate the horizon
topology is
is a periodic coordinate the horizon
topology is 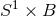 , where
, where 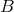 is some
is some 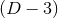 -dimensional manifold.
-dimensional manifold.
Theorem (3.5) can be extended to higher-derivative theories of gravity as follows. Consider a general
theory of gravity coupled to Abelian vectors 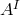 and uncharged scalars
and uncharged scalars 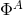 with action
with action
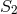 is the 2-derivative action above,
is the 2-derivative action above, 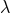 is a coupling constant, and
is a coupling constant, and 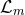 is constructed by
contracting (derivatives of) the Riemann tensor, volume form, scalar fields and Maxwell fields in such a way
that the action is diffeomorphism and gauge-invariant.
is constructed by
contracting (derivatives of) the Riemann tensor, volume form, scalar fields and Maxwell fields in such a way
that the action is diffeomorphism and gauge-invariant.
Proposition 3.1 ([162 ]). Consider an extremal black-hole solution of the above higher-derivative
theory, obeying the same assumptions as in Theorem 3.5. Assume there is a regular horizon when
]). Consider an extremal black-hole solution of the above higher-derivative
theory, obeying the same assumptions as in Theorem 3.5. Assume there is a regular horizon when
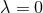 with
with 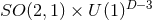 near-horizon symmetry, and the near-horizon solution is analytic
in
near-horizon symmetry, and the near-horizon solution is analytic
in 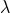 . Then the near-horizon solution has
. Then the near-horizon solution has 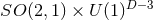 symmetry to all orders in
symmetry to all orders in 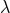 .
.
Hence Theorem 3.5 is stable with respect to higher-derivative corrections. However, it does not apply to
“small” black holes (i.e., if there is no regular black hole for 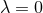 ).
).
So far, the results described all assume  commuting rotational Killing fields. For
commuting rotational Killing fields. For
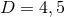 this is the same number as the rank of the rotation group
this is the same number as the rank of the rotation group 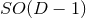 , so the above
results are applicable to asymptotically-flat or globally-AdS black holes. For
, so the above
results are applicable to asymptotically-flat or globally-AdS black holes. For 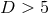 the rank
of this rotation group is
the rank
of this rotation group is 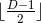 , which is smaller than
, which is smaller than  , so the above theorems do
not apply to asymptotically-flat or AdS black holes. An important open question is whether
the above theorems generalise when fewer than
, so the above theorems do
not apply to asymptotically-flat or AdS black holes. An important open question is whether
the above theorems generalise when fewer than 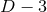 commuting rotational isometries are
assumed, in particular the case with
commuting rotational isometries are
assumed, in particular the case with 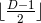 commuting rotational symmetries. To this end,
partial results have been obtained assuming a certain non-Abelian cohomogeneity-1 rotational
isometry.
commuting rotational symmetries. To this end,
partial results have been obtained assuming a certain non-Abelian cohomogeneity-1 rotational
isometry.
Proposition 3.2 ([79 ]). Consider a near-horizon geometry with a rotational isometry group
]). Consider a near-horizon geometry with a rotational isometry group
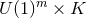 , whose generic orbit on
, whose generic orbit on 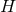 is a cohomogeneity-1
is a cohomogeneity-1 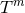 -bundle over a
-bundle over a  -invariant
homogeneous space
-invariant
homogeneous space 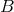 . Furthermore, assume
. Furthermore, assume 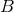 does not admit any
does not admit any  -invariant
one-forms. If Einstein’s equations
-invariant
one-forms. If Einstein’s equations 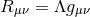 hold, then the near-horizon geometry possesses
a
hold, then the near-horizon geometry possesses
a 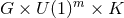 isometry group, where
isometry group, where 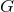 is either
is either 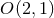 or the 2D Poincaré group.
Furthermore, if
or the 2D Poincaré group.
Furthermore, if 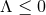 and the near-horizon geometry is non-static then the Poincaré group is
excluded.
and the near-horizon geometry is non-static then the Poincaré group is
excluded.
The assumptions in the above result reduce the Einstein equations for the near-horizon geometry to
ODEs, which can be solved in the same way as in Theorem 3.4. The special case 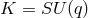 ,
,
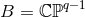 with
with 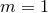 and
and 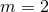 , gives a near-horizon geometry of the type that occurs for a
Myers–Perry black hole with all the angular momenta of set equal in
, gives a near-horizon geometry of the type that occurs for a
Myers–Perry black hole with all the angular momenta of set equal in 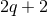 dimensions, or all but one set
equal in
dimensions, or all but one set
equal in 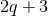 dimensions, respectively.
dimensions, respectively.
The preceding results apply only to cohomogeneity-1 near-horizon geometries. As discussed above, this is
too restrictive to capture the generic case for 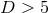 . The following result for higher-cohomogeneity
near-horizon geometries has been shown.
. The following result for higher-cohomogeneity
near-horizon geometries has been shown.
Theorem 3.6 ([166]). Consider a spacetime containing a degenerate horizon invariant under
orthogonally transitive isometry group 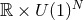 , where
, where 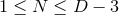 , such that the surfaces
orthogonal to the surfaces of transitivity are simply connected. Then the near-horizon geometry
has an isometry group
, such that the surfaces
orthogonal to the surfaces of transitivity are simply connected. Then the near-horizon geometry
has an isometry group 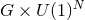 , where
, where 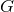 is either
is either 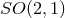 or the 2D Poincaré group.
Furthermore, if the strong energy condition holds and the near-horizon geometry is non-static, the
Poincaré case is excluded.
or the 2D Poincaré group.
Furthermore, if the strong energy condition holds and the near-horizon geometry is non-static, the
Poincaré case is excluded.
The near-horizon geometry in this case can be written as
where as in the above cases we have rescaled the affine parameter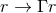 . For the
. For the 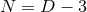 case,
orthogonal transitivity follows from Einstein’s equations [72], which provides another proof of Theorem 3.4
and 3.5. For
case,
orthogonal transitivity follows from Einstein’s equations [72], which provides another proof of Theorem 3.4
and 3.5. For 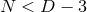 this result guarantees an AdS2 symmetry for all known extremal–black-hole
solutions, since all known explicit solutions possess orthogonally-transitive symmetry groups. In these
higher cohomogeneity cases, the relation between Einstein’s equations and orthogonal transitivity is not
understood. It would be interesting to investigate this further.
this result guarantees an AdS2 symmetry for all known extremal–black-hole
solutions, since all known explicit solutions possess orthogonally-transitive symmetry groups. In these
higher cohomogeneity cases, the relation between Einstein’s equations and orthogonal transitivity is not
understood. It would be interesting to investigate this further.

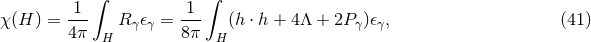
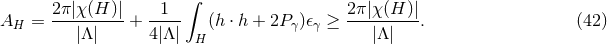
![∫ ′ --H-R-γ′𝜖γ′- E [γ] ≡ ∫ ′ n−n2, (43 ) ( H 𝜖γ )](article401x.gif)
![( ) ∫ 4(n−1)|∇ ϕ|2 + R ϕ2 𝜖 E [ϕ ] ≡--H---n−2-----------γ-----γ. (44 ) γ ( ∫ -2n- ) n−n-2 H ϕn−2𝜖γ](article410x.gif)

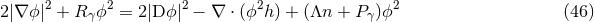
![∫ [ ] ∫ [ ] 4(n-−-1)- 2 2 2 --2n-- 2 2 n − 2 |∇ ϕ| + R γϕ 𝜖γ = 2|D ϕ| + n − 2|∇ϕ | + (nΛ + Pγ)ϕ 𝜖γ. (47 ) H H](article440x.gif)
![∫ ϕ2𝜖γ 2∕n Eγ[ϕ] ≥ − n|Λ|-∫---H2n----n−2 ≥ − n|Λ|A H (48 ) ( H ϕ n−2𝜖γ) n](article456x.gif)


![g = e−λ(x)[A0r2dv2 + 2dvdr ] + γab(x)dxadxb. (51 )](article489x.gif)


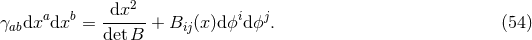



![[ 2 2 ] dx2 ( i i )( j j ) g = Γ (x) A0r dv + 2dvdr + detB--+ Bij(x) dϕ + k rdv dϕ + k rdv , (58 )](article573x.gif)
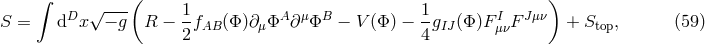
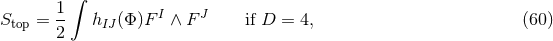
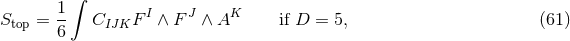
![I [ I I ( i i )] F = d erdv + bi(x ) dϕ + k rdv , (62 )](article614x.gif)
![[ r2 ( r )2] dx2 g = Γ (x) − -2dv2 + 2dvdr + dy1 + --dv + ----- + BIJ (x)dyIdyJ . (63 ) ℓ ℓ B (x)](article637x.gif)

![g = Γ (y)[A0r2dv2 + 2dvdr] + γIJ(y)(dϕI + kIrdv )(d ϕJ + kJrdv ) + γmn (y)dymdyn, (65 )](article688x.gif)