| Occasionally puzzles arise and we spend lectures solving them instead of learning stuff, so I'll try to document them here. I intend to put the solutions up as well
whenever I figure out some nice way of doing that. They're of pretty wildly varying difficulty.
1. Construct a function f with the following properties: 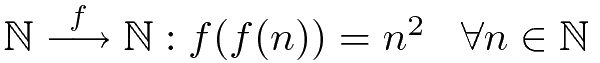
2. By only bending and stretching (no tearing), transform the shape on the left into the one on the right. (Amazing drawings provided by me, puzzles from Intuitive Topology - V. V. Prasolov.) 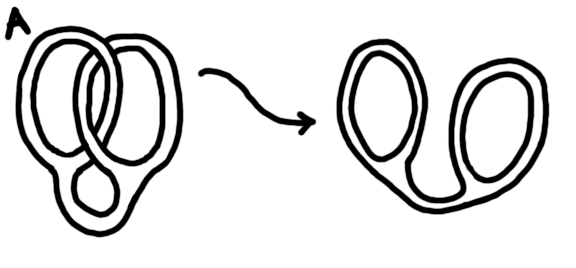
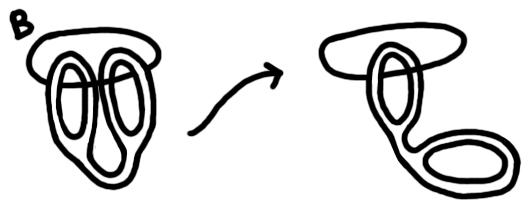
3. Define a function that takes on all real values on all real intervals. (This arose in a talk by Prof. Steven Buckley, NUIM at IMSA 2010. Apparently he got it from a 2nd year analysis problem set from UCC in 1982.) 4. Find all functions with the following properties: 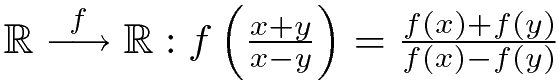
5. Given a cup of coffee and a cup of tea, you then (for some unknown reason) pour a volume of coffee into the tea. You then pour an equivalent volume of tea/coffee mixture back into the coffee. Which cup has more of its original liquid in the end? (A version of this was on a board in the maths department in NUIM, discovered at IMSA.) 6. Explain intuitively (no calculus) why the volume of a cone is 1/3 the volume of the cylinder that would contain it. 7. Given the corners of a square, construct a path between them such that the length of the path is a minimum. Then extend this to higher dimensions. 8. Holditch's Theorem says, take a curve, draw a chord on it of constant length. Put a point on the chord dividing it into lengths p and q. If the chord is then slid around the curve, the point will draw out a secondary curve, the area between which and the original curve is equal to πpq. The problem is to find the necessary conditions placed on the original curve for this to be valid. In the mean time, project euler. I was using this as a reason to learn Haskell some time ago, but gave up and forgot most of it. |









|