Another factor which can seriously affect the rate of convergence, and the mixing of the chain is the shape of the posterior distribution. Jarner [20] has considered in detail the theoretical speed of convergence for different shapes of the posterior, his work building on theoretical work of Roberts [43]. This phenomenon was observed in practice, in the context of the sampling in the models presented later on.
An example demonstrates what occurred. Consider a two dimensional
posterior, 
which is a ridge,
as illustrated in Figure 
. The methods described
sample the posterior, by starting at some location in the plane,
and moving first in the x direction, then in the y direction.
Each move is either accepted or rejected. It is clear from
Figure that the methods will take a substantial
amount of time to move from the lower left to the upper right of
the target density. In Section it is mentioned
that the chain took a very large number of steps to examine the
posterior, and that this difficulty could have been avoided. The
difficulty presented is that the chain takes many steps to sample
from the complete support of the distribution; that is the chain
does not mix well.
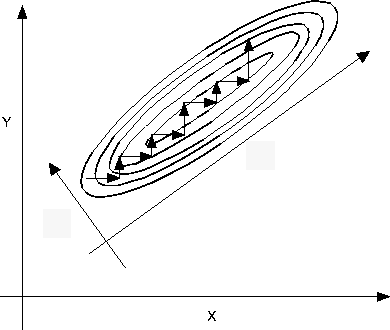
Figure: Posterior Density in x and y.
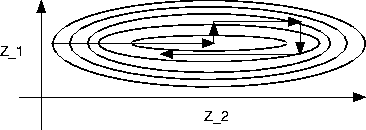
Figure: Transformed Density with Better
Mixing in 
and 
.
A reparameterisation of the problem allows a much quicker sampling
strategy. Consider the reparameterisation shown in
Figure . The transformation 
yields a basis for which the density is now a ridge
running in the direction of only, with width along the
direction. The samplers now have the ability to traverse the
target in just one step of z.
Of course, in order to carry out such a reparameterisation, one needs to have knowledge of the posterior distribution. As such, the transformation may not in general be specified a priori. It therefore requires an initial running of the chain with untransformed variables and based on this a transformation can be made. In the case of the models discussed later it was found that the transformation speeded up convergence by an order of magnitude.