Let 
be the distribution of interest. Let 
be
the Markov matrix to be constructed. Now, what is needed is a
method of constructing so that it is indeed a Markov
Matrix, and that the stationary distribution of this Matrix is
, the distribution of interest.
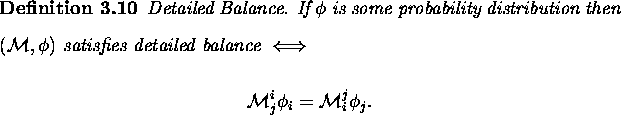
This property yields a method of constructing a suitable matrix, by using the result of the following theorem.
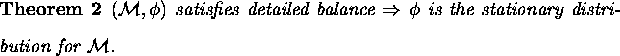
Proof: since
and this is true 
thus 
, that is
is the stationary distribution for 
. So, given a
distribution, 
, it is possible to construct a Markov matrix
with as the stationary distribution, by imposing the
condition of detailed balance.
That is, if are chosen so that 
, and of course subject to the constraints that
and 
, and that the
matrix is aperiodic irreducible, then is a transition
matrix for a Markov chain whose equilibrium distribution is 
.
The details of how one might go about such a construction are
given in the Metropolis-Hastings Algorithm [30]
[19].