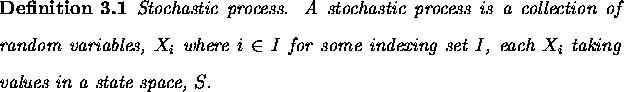
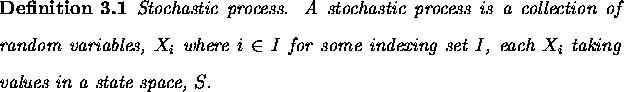
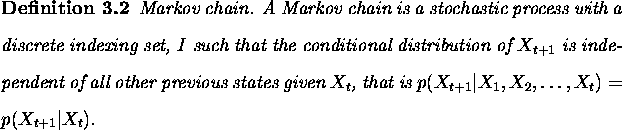
For simplicity, theory and details are given for a discrete state space, S.
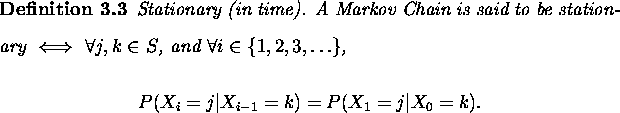
A stationary Markov chain is sometimes referred to as homogeneous in time, since, by definition, the probability of moving between two states remains constant in time.
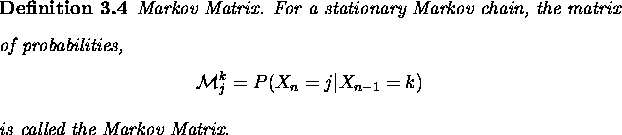
Note that this definition is independent of n (stationarity),
that the entries in the Matrix are 
(probabilities) and
that 
, since the chain must
move to some state, j. This is sometimes called a transition
matrix, and the associated probabilities transition probabilities.
It is also worth noting that the matrix 
is the matrix of probabilities 
.
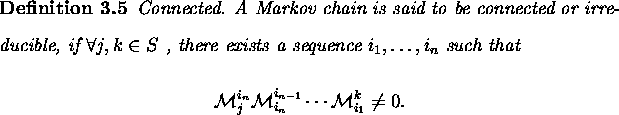
That is, there is a non-zero probability of going to state j from state k in n steps, for some n.
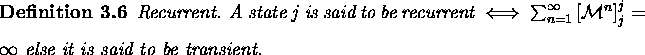
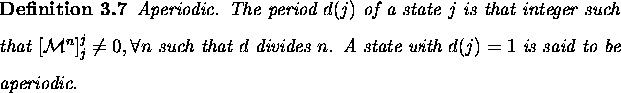
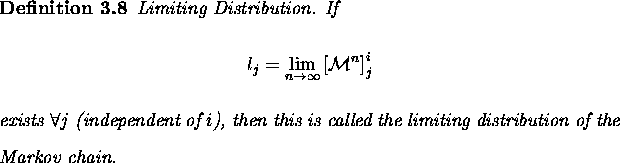
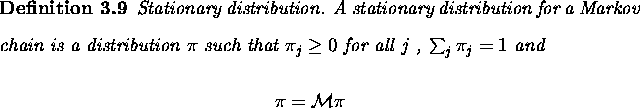
The stationary distribution is also referred to as the invariant distribution or equilibrium distribution of a Markov chain.
Recall the discussion above regarding stratified and importance sampling. If it were possible to construct a Markov chain that would visit each category the `correct' number of times, then this method could be used to sample from the distribution of interest. In practice, what `correct' means here, is that the equilibrium distribution of the Markov chain is the same as the distribution of interest. In a sense this is the reverse of the theory above, since the distribution of interest is known, and the Markov chain needs to be constructed.
It is possible to do this, under certain conditions, and there are a number of ways of doing it. Of primary interest will be the approach of Metropolis-Hastings.