Metropolis Hastings

The Metropolis-Hastings algorithm is a Markov chain Monte Carlo method as described previously. The algorithm sets about constructing a Markov matrix which has as its equilibrium distribution some target density , of interest to the operator. The algorithm requires the specification of a proposal density, , which is a probability density for j and may depend upon i. This is then used in order to propose transitions from i. The condition of detailed balance is then imposed in the following fashion.

Construct by imposing detailed balance, so that the matrix with entries given by is a Markov matrix. This is done as follows:

Otherwise, assume (without loss of generality) that

then setting , and constructing

detailed balance holds.

Thus, by defining in general

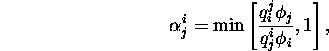
detailed balance is satisfied.

In order that what has been constructed is a Markov matrix which will generate a chain having as the invariant distribution, it remains to show that is indeed Markov. This imposes conditions on the form of q which is related in turn to . The conditions are as referred to before, aperiodicity and connectedness. These are indeed satisfied for quite a large family of densities [30], [54].

The algorithm then, works as follows;

1. Set i = 0; Set N = some large value; Choose an initial state .
2. Propose y from .
3. Accept the proposal with probability .
4. If accepted, set , else set .
5. If i<N set i=i+1; and back to step 2.

Although theory demonstrates that a chain constructed using this algorithm has a limiting distribution which is the target distribution, the question of the rate at which the limiting distribution is attained is still open.

Note that the samples generated by the chain will depend upon the choice of and only when close to the limiting distribution are the samples to be considered as having come from the target distribution.

What size should N be, and for what minimum j should be considered as a sample from the target? A number of methods have been proposed in order to answer these questions. Diagnostic methods of Gelman and Rubin [18] and others are reviewed by Cowles and Carlin [11]. Murdoch and Green have developed methods of demonstrating convergence [35], but these methods are far less practical than the heuristic diagnostics described elsewhere. A review of methods to date including those of Murdoch and Green is provided by Brooks and Roberts [7].

The Metropolis-Hastings algorithm is valid for sampling from the , for , that is for a general vector, x. However, in practice it can be more natural to consider x as the combination of subvectors . It turns out [9] that a transition matrix for a chain which converges to the target may be constructed by considering matrices for a chain which samples from and .