Kernel density estimation consists of estimating a posterior
density for a function of interest, using samples from the
posterior, often drawn using one of the numerical techniques. Let
be samples from the posterior
distribution 
. If one is interested in the
properties of the posterior density function 
, where
conditional on 
, X is independent of 
, that is
, the following result is useful;
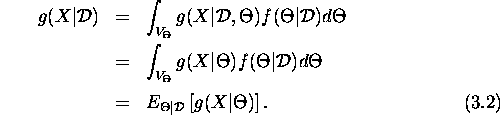
This expected value may be approximated in the usual fashion, as a
simple numerical average of the values of the function at each of
the sample points. That is using 
given by
The fact that is a density function follows from the
fact that each of the 
is a density function.
Kernel density estimation is a standard method of examining
posterior distributions, and properties of functions of the
parameters.