Consider the case of drawing from a population of unknown mean,
, but known variance 
. ( 
is termed
precision, and is just the reciprocal of variance.)
The model is that the data, X, will be normally distributed with unknown mean but given variance. Thus, in terms of a single observation, x, we can write down the likelihood;
The next step is to elicit a prior for . It may be reasonable
to assume that the prior beliefs about can be expressed as a
normal distribution, that is
where both 
and 
are specified.
Typically is the expected location of , and
is an expression of how precise that estimate is.
In general, will be small.
Thus, having collected data, it is possible to derive the posterior for
according to Bayes theorem for random variables;
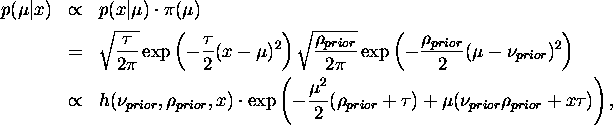
where 
is independent of . Defining
and multiplying by
which is
independent of , the above is
which reduces to
which is the form of the normal density with mean 
and
precision 
. Thus, in the case of inference for the
unknown mean, with normal prior, the posterior is normal. This
simple form of the posterior depends on the choice of the prior,
given the likelihood. The choice of prior that leads to the simple
posterior, is called a conjugate prior; more formally, given a
likelihood, 
, then a prior chosen from a family of
densities, such that the posterior is also from that family, is
said to be conjugate.
As can be seen from the above, in the case of conjugate densities, the problem of obtaining a posterior is simplified [5]. However, this is only appropriate where the chosen prior distribution, with suitable parameters can accurately represent the prior knowledge. The alternative is to use numerical techniques to obtain the properties of interest from the posterior distribution.
The question of prior elicitation is one that needs mentioning also. Apart from the philosophical difficulties that many have with prior probabilities, there are practical problems which need addressing.