The growth of cracks is modelled using the growth model. Based upon the coalescence
model already discussed, and following the methods used in the analysis of crack
formation in PMMA [29], the rate of coalescence is modelled using a
Poisson process. The modelling of which cracks are involved in coalescence is
dependent upon the spatial distribution of cracks, and is really a question of
modelling 
. In this context, spatial data
was unavailable, and the probability of being involved in coalescence was assumed to
be 
for all cracks, that is, assumed to be discrete uniform.
The model used is represented by a directed graph in
Figure 
for an example of three cracks involved in a
coalescence. The important feature of the DAG is the dependence of
the new crack on the two previous cracks, or in particular, the
parameters for the previous cracks. There are no cyclic
dependencies in the graph.
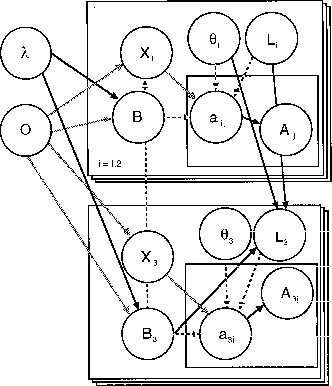
Figure: DAG for Joint Coalescence and Growth Model for Example.
In the DAG, the model for growth is the same as the model in Chapter .
The new parameters are 
which are the times of birth, death and length
at birth respectively for each crack. The hyperparameters are 
which
represent the rate of a Poisson, and an order for births and deaths, which also
determines which cracks coalesce with which. The times of birth and death are
realisations from the Poisson process. Of course these will not be observed, but they
are an important part of the model.
The dependence of the initial length of crack 3 on the parameters and initial lengths of cracks 1 and 2 and their parameters is modelled as the sum of the computed values from the differential equation governing growth at time of birth with random noise.
The model represented by this DAG is valid for the total data. This would obviously be much larger than that for just three cracks. The links depend on which cracks coalesce, and in the full DAG, there are still no cycles.