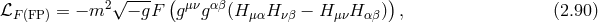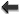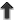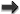2 Massive and Interacting Fields
2.1 Proca field
2.1.1 Maxwell kinetic term
Before jumping into the subtleties of massive spin-2 field and gravity in general, we start this review with
massless and massive spin-1 fields as a warm up. Consider a Lorentz vector field 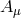 living on a
four-dimensional Minkowski manifold. We focus this discussion to four dimensions and the
extension to
living on a
four-dimensional Minkowski manifold. We focus this discussion to four dimensions and the
extension to 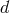 dimensions is straightforward. Restricting ourselves to Lorentz invariant and
local actions for now, the kinetic term can be decomposed into three possible contributions:
dimensions is straightforward. Restricting ourselves to Lorentz invariant and
local actions for now, the kinetic term can be decomposed into three possible contributions:
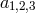 are so far arbitrary dimensionless coefficients and the possible kinetic terms are given by
where in this section, indices are raised and lowered with respect to the flat Minkowski metric. The first and
third contributions are equivalent up to a boundary term, so we set
are so far arbitrary dimensionless coefficients and the possible kinetic terms are given by
where in this section, indices are raised and lowered with respect to the flat Minkowski metric. The first and
third contributions are equivalent up to a boundary term, so we set 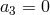 without loss of
generality.
without loss of
generality.
We now proceed to establish the behavior of the different degrees of freedom (dofs) present in this
theory. A priori, a Lorentz vector field 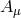 in four dimensions could have up to four dofs, which we can
split as a transverse contribution
in four dimensions could have up to four dofs, which we can
split as a transverse contribution 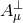 satisfying
satisfying 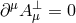 bearing a priori three dofs and a longitudinal
mode
bearing a priori three dofs and a longitudinal
mode  with
with 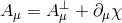 .
.
Helicity-0 mode
Focusing on the longitudinal (or helicity-0) mode 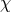 , the kinetic term takes the form
, the kinetic term takes the form
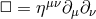 represents the d’Alembertian in flat Minkowski space and the second equality holds
after integrations by parts. We directly see that unless
represents the d’Alembertian in flat Minkowski space and the second equality holds
after integrations by parts. We directly see that unless 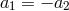 , the kinetic term for the field
, the kinetic term for the field
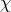 bears higher time (and space) derivatives. As a well known consequence of Ostrogradsky’s
theorem [421], two dofs are actually hidden in
bears higher time (and space) derivatives. As a well known consequence of Ostrogradsky’s
theorem [421], two dofs are actually hidden in 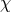 with an opposite sign kinetic term. This can be
seen by expressing the propagator
with an opposite sign kinetic term. This can be
seen by expressing the propagator  as the sum of two propagators with opposite signs:
signaling that one of the modes always couples the wrong way to external sources. The mass
as the sum of two propagators with opposite signs:
signaling that one of the modes always couples the wrong way to external sources. The mass 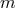 of this
mode is arbitrarily low which implies that the theory (2.1*) with
of this
mode is arbitrarily low which implies that the theory (2.1*) with  and
and 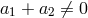 is always sick. Alternatively, one can see the appearance of the Ostrogradsky instability by
introducing a Lagrange multiplier
is always sick. Alternatively, one can see the appearance of the Ostrogradsky instability by
introducing a Lagrange multiplier 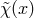 , so that the kinetic action (2.5*) for
, so that the kinetic action (2.5*) for  is equivalent to
after integrating out the Lagrange
multiplier2
is equivalent to
after integrating out the Lagrange
multiplier2
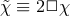 . We can now perform the change of variables
. We can now perform the change of variables 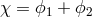 and
and 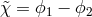 giving the
resulting Lagrangian for the two scalar fields
giving the
resulting Lagrangian for the two scalar fields 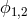 As a result, the two scalar fields
As a result, the two scalar fields 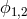 always enter with opposite kinetic terms, signaling that one of them is always
a ghost.3
The only way to prevent this generic pathology is to make the specific choice
always enter with opposite kinetic terms, signaling that one of them is always
a ghost.3
The only way to prevent this generic pathology is to make the specific choice 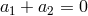 , which
corresponds to the well-known Maxwell kinetic term.
, which
corresponds to the well-known Maxwell kinetic term.
Helicity-1 mode and gauge symmetry
Now that the form of the local and covariant kinetic term has been uniquely established by the requirement
that no ghost rides on top of the helicity-0 mode, we focus on the remaining transverse mode 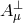 ,
,
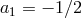 . As a result, the only possible local kinetic term for a
spin-1 field is the Maxwell one:
with
. As a result, the only possible local kinetic term for a
spin-1 field is the Maxwell one:
with 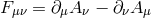 . Restricting ourselves to a massless spin-1 field (with no potential and
other interactions), the resulting Maxwell theory satisfies the following
. Restricting ourselves to a massless spin-1 field (with no potential and
other interactions), the resulting Maxwell theory satisfies the following 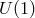 gauge symmetry:
This gauge symmetry projects out two of the naive four degrees of freedom. This can be seen at the level of
the Lagrangian directly, where the gauge symmetry (2.11*) allows us to fix the gauge of our choice. For
convenience, we perform a
gauge symmetry:
This gauge symmetry projects out two of the naive four degrees of freedom. This can be seen at the level of
the Lagrangian directly, where the gauge symmetry (2.11*) allows us to fix the gauge of our choice. For
convenience, we perform a 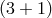 -split and choose Coulomb gauge
-split and choose Coulomb gauge 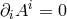 , so that only two dofs are
present in
, so that only two dofs are
present in 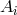 , i.e.,
, i.e., 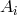 contains no longitudinal mode,
contains no longitudinal mode, 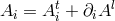 , with
, with 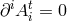 and the
Coulomb gauge sets the longitudinal mode
and the
Coulomb gauge sets the longitudinal mode 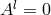 . The time-component
. The time-component 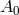 does not exhibit a kinetic
term,
and appears instead as a Lagrange multiplier imposing the constraint
The Maxwell action has therefore only two propagating dofs in
does not exhibit a kinetic
term,
and appears instead as a Lagrange multiplier imposing the constraint
The Maxwell action has therefore only two propagating dofs in 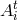 ,
To summarize, the Maxwell kinetic term for a vector field and the fact that a massless vector field in four
dimensions only propagates 2 dofs is not a choice but has been imposed upon us by the requirement that no
ghost rides along with the helicity-0 mode. The resulting theory is enriched by a
,
To summarize, the Maxwell kinetic term for a vector field and the fact that a massless vector field in four
dimensions only propagates 2 dofs is not a choice but has been imposed upon us by the requirement that no
ghost rides along with the helicity-0 mode. The resulting theory is enriched by a 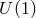 gauge symmetry
which in turn freezes the helicity-0 mode when no mass term is present. We now ‘promote’ the theory to a
massive vector field.
gauge symmetry
which in turn freezes the helicity-0 mode when no mass term is present. We now ‘promote’ the theory to a
massive vector field.
2.1.2 Proca mass term
Starting with the Maxwell action, we consider a covariant mass term 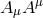 corresponding to the Proca
action
corresponding to the Proca
action
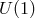 gauge symmetry (2.11*), so that the Coulomb gauge can no longer be chosen and the
longitudinal mode is now dynamical. To see this, let us use the previous decomposition
gauge symmetry (2.11*), so that the Coulomb gauge can no longer be chosen and the
longitudinal mode is now dynamical. To see this, let us use the previous decomposition 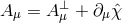 and notice that the mass term now introduces a kinetic term for the helicity-0 mode
and notice that the mass term now introduces a kinetic term for the helicity-0 mode 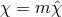 ,
A massive vector field thus propagates three dofs, namely two in the transverse modes
,
A massive vector field thus propagates three dofs, namely two in the transverse modes 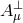 and one in the
longitudinal mode
and one in the
longitudinal mode 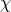 . Physically, this can be understood by the fact that a massive vector field does not
propagate along the light-cone, and the fluctuations along the line of propagation correspond to an
additional physical dof.
. Physically, this can be understood by the fact that a massive vector field does not
propagate along the light-cone, and the fluctuations along the line of propagation correspond to an
additional physical dof.
Before moving to the Abelian Higgs mechanism, which provides a dynamical way to give a mass to
bosons, we first comment on the discontinuity in number of dofs between the massive and massless case.
When considering the Proca action (2.16*) with the properly normalized fields 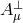 and
and 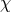 , one does not
recover the massless Maxwell action (2.9*) or (2.10*) when sending the boson mass
, one does not
recover the massless Maxwell action (2.9*) or (2.10*) when sending the boson mass 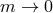 . A priori, this
seems to signal the presence of a discontinuity which would allow us to distinguish between
for instance a massless photon and a massive one no matter how tiny the mass. In practice,
however, the difference is physically indistinguishable so long as the photon couples to external
sources in a way which respects the
. A priori, this
seems to signal the presence of a discontinuity which would allow us to distinguish between
for instance a massless photon and a massive one no matter how tiny the mass. In practice,
however, the difference is physically indistinguishable so long as the photon couples to external
sources in a way which respects the 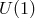 symmetry. Note however that quantum anomalies
remain sensitive to the mass of the field so the discontinuity is still present at this level, see
Refs. [197, 204].
symmetry. Note however that quantum anomalies
remain sensitive to the mass of the field so the discontinuity is still present at this level, see
Refs. [197, 204].
To physically tell the difference between a massless vector field and a massive one with tiny mass, one has to probe the system, or in other words include interactions with external sources
The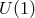 symmetry present in the massless case is preserved only if the external sources are conserved,
symmetry present in the massless case is preserved only if the external sources are conserved,
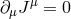 . Such a source produces a vector field which satisfies
in the massless case. The exchange amplitude between two conserved sources
. Such a source produces a vector field which satisfies
in the massless case. The exchange amplitude between two conserved sources 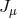 and
and 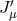 mediated by a
massless vector field is given by
On the other hand, if the vector field is massive, its response to the source
mediated by a
massless vector field is given by
On the other hand, if the vector field is massive, its response to the source 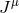 is instead
In that case, one needs to consider both the transverse and the longitudinal modes of the vector field in the
exchange amplitude between the two sources
is instead
In that case, one needs to consider both the transverse and the longitudinal modes of the vector field in the
exchange amplitude between the two sources 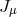 and
and 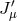 . Fortunately, a conserved source does not excite
the longitudinal mode and the exchange amplitude is uniquely given by the transverse mode,
As a result, the exchange amplitude between two conserved sources is the same in the limit
. Fortunately, a conserved source does not excite
the longitudinal mode and the exchange amplitude is uniquely given by the transverse mode,
As a result, the exchange amplitude between two conserved sources is the same in the limit 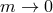 no
matter whether the vector field is intrinsically massive and propagates 3 dofs or if it is massless and only
propagates 2 modes. It is, therefore, impossible to probe the difference between an exactly massive vector
field and a massive one with arbitrarily small mass.
no
matter whether the vector field is intrinsically massive and propagates 3 dofs or if it is massless and only
propagates 2 modes. It is, therefore, impossible to probe the difference between an exactly massive vector
field and a massive one with arbitrarily small mass.
Notice that in the massive case no 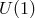 symmetry is present and the source needs not be conserved.
However, the previous argument remains unchanged so long as
symmetry is present and the source needs not be conserved.
However, the previous argument remains unchanged so long as 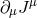 goes to zero in the massless limit
at least as quickly as the mass itself. If this condition is violated, then the helicity-0 mode
ought to be included in the exchange amplitude (2.21*). In parallel, in the massless case the
non-conserved source provides a new kinetic term for the longitudinal mode which then becomes
dynamical.
goes to zero in the massless limit
at least as quickly as the mass itself. If this condition is violated, then the helicity-0 mode
ought to be included in the exchange amplitude (2.21*). In parallel, in the massless case the
non-conserved source provides a new kinetic term for the longitudinal mode which then becomes
dynamical.
2.1.3 Abelian Higgs mechanism for electromagnetism
Associated with the absence of an intrinsic discontinuity in the massless limit is the existence of a Higgs mechanism for the vector field whereby the vector field acquires a mass dynamically. As we shall see later, the situation is different for gravity where no equivalent dynamical Higgs mechanism has been discovered to date. Nevertheless, the tools used to describe the Abelian Higgs mechanism and in particular the introduction of a Stückelberg field will prove useful in the gravitational case as well.
To describe the Abelian Higgs mechanism, we start with a vector field 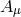 with associated Maxwell
tensor
with associated Maxwell
tensor  and a complex scalar field
and a complex scalar field 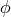 with quartic potential
with quartic potential
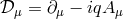 ensures the existence of the
ensures the existence of the 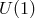 symmetry, which in
addition to (2.11*) shifts the scalar field as
Splitting the complex scalar field
symmetry, which in
addition to (2.11*) shifts the scalar field as
Splitting the complex scalar field 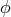 into its norm and phase
into its norm and phase 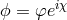 , we see that the covariant
derivative plays the role of the mass term for the vector field, when scalar field acquires a non-vanishing
vacuum expectation value (vev),
The Higgs field
, we see that the covariant
derivative plays the role of the mass term for the vector field, when scalar field acquires a non-vanishing
vacuum expectation value (vev),
The Higgs field 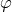 can be made arbitrarily massive by setting
can be made arbitrarily massive by setting 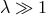 in such a way that its dynamics
may be neglected and the field can be treated as frozen at
in such a way that its dynamics
may be neglected and the field can be treated as frozen at 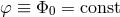 . The resulting theory is that of
a massive vector field,
where the phase
. The resulting theory is that of
a massive vector field,
where the phase 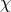 of the complex scalar field plays the role of a Stückelberg which restores the
of the complex scalar field plays the role of a Stückelberg which restores the 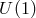 gauge symmetry in the massive case,
In this formalism, the
gauge symmetry in the massive case,
In this formalism, the 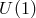 gauge symmetry is restored at the price of introducing explicitly a
Stückelberg field which transforms in such a way so as to make the mass term invariant. The symmetry
ensures that the vector field
gauge symmetry is restored at the price of introducing explicitly a
Stückelberg field which transforms in such a way so as to make the mass term invariant. The symmetry
ensures that the vector field 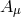 propagates only 2 dofs, while the Stückelberg
propagates only 2 dofs, while the Stückelberg 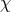 propagates the third
dof. While no equivalent to the Higgs mechanism exists for gravity, the same Stückelberg trick to
restore the symmetry can be used in that case. Since the in that context the symmetry broken
is coordinate transformation invariance, (full diffeomorphism invariance or covariance), four
Stückelberg fields should in principle be included in the context of massive gravity, as we shall see
below.
propagates the third
dof. While no equivalent to the Higgs mechanism exists for gravity, the same Stückelberg trick to
restore the symmetry can be used in that case. Since the in that context the symmetry broken
is coordinate transformation invariance, (full diffeomorphism invariance or covariance), four
Stückelberg fields should in principle be included in the context of massive gravity, as we shall see
below.
2.1.4 Interacting spin-1 fields
Now that we have introduced the notion of a massless and a massive spin-1 field, let us look at 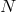 interacting spin-1 fields. We start with
interacting spin-1 fields. We start with 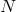 free and massless gauge fields,
free and massless gauge fields, 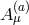 , with
, with 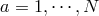 , and
respective Maxwell tensors
, and
respective Maxwell tensors 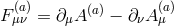 ,
,
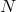 copies of
copies of 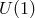 , (i.e., the symmetry group
is
, (i.e., the symmetry group
is 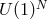 which is Abelian as opposed to
which is Abelian as opposed to 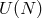 which would correspond to a Yang–Mills theory and
would not be Abelian).
which would correspond to a Yang–Mills theory and
would not be Abelian).
However, in addition to these 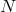 gauge invariances, the kinetic term is invariant under global rotations
in field space,
gauge invariances, the kinetic term is invariant under global rotations
in field space,
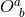 is a (global) rotation matrix. Now let us consider some interactions between these different
fields. At the linear level (quadratic level in the action), the most general set of interactions is
where
is a (global) rotation matrix. Now let us consider some interactions between these different
fields. At the linear level (quadratic level in the action), the most general set of interactions is
where 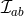 is an arbitrary symmetric matrix with constant coefficients. For an arbitrary rank-N matrix, all
is an arbitrary symmetric matrix with constant coefficients. For an arbitrary rank-N matrix, all
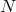 copies of
copies of 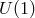 are broken, and the theory then propagates
are broken, and the theory then propagates 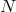 additional helicity-0
modes, for a total of
additional helicity-0
modes, for a total of 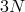 independent polarizations in four spacetime dimensions. However, if
the rank
independent polarizations in four spacetime dimensions. However, if
the rank  of
of 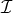 is
is 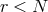 , i.e., if some of the eigenvalues of
, i.e., if some of the eigenvalues of 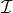 vanish, then there are
vanish, then there are
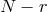 special directions in field space which receive no interactions, and the theory thus keeps
special directions in field space which receive no interactions, and the theory thus keeps
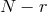 independent copies of
independent copies of 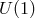 . The theory then propagates
. The theory then propagates  massive spin-1 fields
and
massive spin-1 fields
and  massless spin-2 fields, for a total of
massless spin-2 fields, for a total of 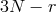 independent polarizations in four
dimensions.
independent polarizations in four
dimensions.
We can see this statement more explicitly in the case of 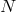 spin-1 fields by diagonalizing the mass
matrix
spin-1 fields by diagonalizing the mass
matrix 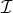 . A mentioned previously, the kinetic term is invariant under field space rotations, (2.29*), so one
can use this freedom to work in a field representation where the mass matrix
. A mentioned previously, the kinetic term is invariant under field space rotations, (2.29*), so one
can use this freedom to work in a field representation where the mass matrix 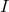 is diagonal,
is diagonal,
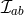 .
.
2.2 Spin-2 field
As we have seen in the case of a vector field, as long as it is local and Lorentz-invariant, the kinetic term is uniquely fixed by the requirement that no ghost be present. Moving now to a spin-2 field, the same argument applies exactly and the Einstein–Hilbert term appears naturally as the unique kinetic term free of any ghost-like instability. This is possible thanks to a symmetry which projects out all unwanted dofs, namely diffeomorphism invariance (linear diffs at the linearized level, and non-linear diffs/general covariance at the non-linear level).
2.2.1 Einstein–Hilbert kinetic term
We consider a symmetric Lorentz tensor field 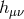 . The kinetic term can be decomposed into four possible
local contributions (assuming Lorentz invariance and ignoring terms which are equivalent upon integration
by parts):
. The kinetic term can be decomposed into four possible
local contributions (assuming Lorentz invariance and ignoring terms which are equivalent upon integration
by parts):
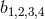 are dimensionless coefficients which are to be determined in the same way as for the
vector field. We split the 10 components of the symmetric tensor field
are dimensionless coefficients which are to be determined in the same way as for the
vector field. We split the 10 components of the symmetric tensor field 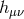 into a transverse
tensor
into a transverse
tensor 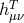 (which carries 6 components) and a vector field
(which carries 6 components) and a vector field 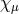 (which carries 4 components),
Just as in the case of the spin-1 field, an arbitrary kinetic term of the form (2.32*) with untuned coefficients
(which carries 4 components),
Just as in the case of the spin-1 field, an arbitrary kinetic term of the form (2.32*) with untuned coefficients
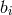 would contain higher derivatives for
would contain higher derivatives for 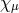 which in turn would imply a ghost. As we shall
see below, avoiding a ghost within the kinetic term automatically leads to gauge-invariance.
After substitution of
which in turn would imply a ghost. As we shall
see below, avoiding a ghost within the kinetic term automatically leads to gauge-invariance.
After substitution of 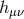 in terms of
in terms of 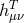 and
and 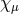 , the potentially dangerous parts are
Preventing these higher derivative terms from arising sets
or in other words, the unique (local and Lorentz-invariant) kinetic term one can write for a spin-2 field is
the Einstein–Hilbert term
where
, the potentially dangerous parts are
Preventing these higher derivative terms from arising sets
or in other words, the unique (local and Lorentz-invariant) kinetic term one can write for a spin-2 field is
the Einstein–Hilbert term
where 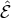 is the Lichnerowicz operator
and we have set
is the Lichnerowicz operator
and we have set 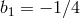 to follow standard conventions. As a result, the kinetic term for the tensor
field
to follow standard conventions. As a result, the kinetic term for the tensor
field 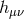 is invariant under the following gauge transformation,
We emphasize that the form of the kinetic term and its gauge invariance is independent on whether or not
the tensor field has a mass, (as long as we restrict ourselves to a local and Lorentz-invariant kinetic term).
However, just as in the case of a massive vector field, this gauge invariance cannot be maintained by a mass
term or any other self-interacting potential. So only in the massless case, does this symmetry remain exact.
Out of the 10 components of a tensor field, the gauge symmetry removes
is invariant under the following gauge transformation,
We emphasize that the form of the kinetic term and its gauge invariance is independent on whether or not
the tensor field has a mass, (as long as we restrict ourselves to a local and Lorentz-invariant kinetic term).
However, just as in the case of a massive vector field, this gauge invariance cannot be maintained by a mass
term or any other self-interacting potential. So only in the massless case, does this symmetry remain exact.
Out of the 10 components of a tensor field, the gauge symmetry removes 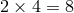 of them, leaving a
massless tensor field with only two propagating dofs as is well known from the propagation of gravitational
waves in four dimensions.
of them, leaving a
massless tensor field with only two propagating dofs as is well known from the propagation of gravitational
waves in four dimensions.
In 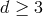 spacetime dimensions, gravitational waves have
spacetime dimensions, gravitational waves have 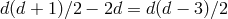 independent
polarizations. This means that in three dimensions there are no gravitational waves and in five dimensions
they have five independent polarizations.
independent
polarizations. This means that in three dimensions there are no gravitational waves and in five dimensions
they have five independent polarizations.
2.2.2 Fierz–Pauli mass term
As seen in seen in Section 2.2.1, for a local and Lorentz-invariant theory, the linearized kinetic term is uniquely fixed by the requirement that longitudinal modes propagate no ghost, which in turn prevents that operator from exciting these modes altogether. Just as in the case of a massive spin-1 field, we shall see in what follows that the longitudinal modes can nevertheless be excited when including a mass term. In what follows we restrict ourselves to linear considerations and spare any non-linearity discussions for Parts I and II. See also [327] for an analysis of the linearized Fierz–Pauli theory using Bardeen variables.
In the case of a spin-2 field 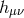 , we are a priori free to choose between two possible mass
terms
, we are a priori free to choose between two possible mass
terms 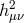 and
and 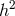 , so that the generic mass term can be written as a combination of both,
, so that the generic mass term can be written as a combination of both,
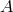 is a dimensionless parameter. Just as in the case of the kinetic term, the stability of the theory
constrains very strongly the phase space and we shall see that only for
is a dimensionless parameter. Just as in the case of the kinetic term, the stability of the theory
constrains very strongly the phase space and we shall see that only for  is the theory stable at that
order. The presence of this mass term breaks diffeomorphism invariance. Restoring it requires the
introduction of four Stückelberg fields
is the theory stable at that
order. The presence of this mass term breaks diffeomorphism invariance. Restoring it requires the
introduction of four Stückelberg fields 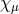 which transform under linear diffeomorphisms in
such a way as to make the mass term invariant, just as in the Abelian-Higgs mechanism for
electromagnetism [174]. Including the four linearized Stückelberg fields, the resulting mass term
is invariant under the simultaneous transformations:
This mass term then provides a kinetic term for the Stückelberg fields
which is precisely of the same form as the kinetic term considered for a spin-1 field (2.1*) in Section 2.1.1
with
which transform under linear diffeomorphisms in
such a way as to make the mass term invariant, just as in the Abelian-Higgs mechanism for
electromagnetism [174]. Including the four linearized Stückelberg fields, the resulting mass term
is invariant under the simultaneous transformations:
This mass term then provides a kinetic term for the Stückelberg fields
which is precisely of the same form as the kinetic term considered for a spin-1 field (2.1*) in Section 2.1.1
with 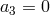 and
and 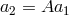 . Now the same logic as in Section 2.1.1 applies and singling out the
longitudinal component of these Stückelberg fields it follows that the only combination which does not
involve higher derivatives is
. Now the same logic as in Section 2.1.1 applies and singling out the
longitudinal component of these Stückelberg fields it follows that the only combination which does not
involve higher derivatives is 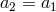 or in other words
or in other words 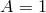 . As a result, the only possible mass term
one can consider which is free from an Ostrogradsky instability is the Fierz–Pauli mass term
In unitary gauge, i.e., in the gauge where the Stückelberg fields
. As a result, the only possible mass term
one can consider which is free from an Ostrogradsky instability is the Fierz–Pauli mass term
In unitary gauge, i.e., in the gauge where the Stückelberg fields 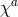 are set to zero, the Fierz–Pauli mass
term simply reduces to
where once again the indices are raised and lowered with respect to the Minkowski metric.
are set to zero, the Fierz–Pauli mass
term simply reduces to
where once again the indices are raised and lowered with respect to the Minkowski metric.
Propagating degrees of freedom
To identify the propagating degrees of freedom we may split 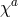 further into a transverse and a
longitudinal mode,
further into a transverse and a
longitudinal mode,
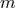 has been introduced for further convenience).
has been introduced for further convenience).
In terms of 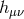 and the Stückelberg fields
and the Stückelberg fields 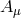 and
and 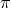 the linearized Fierz–Pauli action is
the linearized Fierz–Pauli action is
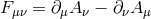 and
and 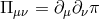 and all the indices are raised and lowered with respect to
the Minkowski metric.
and all the indices are raised and lowered with respect to
the Minkowski metric.
Terms on the first line represent the kinetic terms for the different fields while the second line represent the mass terms and mixing.
We see that the kinetic term for the field 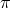 is hidden in the mixing with
is hidden in the mixing with 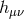 . To make the field
content explicit, we may diagonalize this mixing by shifting
. To make the field
content explicit, we may diagonalize this mixing by shifting 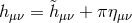 and the linearized
Fierz–Pauli action is
and the linearized
Fierz–Pauli action is
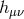 represents the helicity-2 mode as already present in GR and propagates 2 dofs,
represents the helicity-2 mode as already present in GR and propagates 2 dofs,
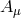 represents the helicity-1 mode and propagates 2 dofs, and finally
represents the helicity-1 mode and propagates 2 dofs, and finally 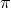 represents the helicity-0 mode
and propagates 1 dof, leading to a total of five dofs as is to be expected for a massive spin-2 field in four
dimensions.
represents the helicity-0 mode
and propagates 1 dof, leading to a total of five dofs as is to be expected for a massive spin-2 field in four
dimensions.
The degrees of freedom have not yet been split into their mass eigenstates but on doing
so one can easily check that all the degrees of freedom have the same positive mass square
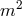 .
.
Most of the phenomenology and theoretical consistency of massive gravity is related to the dynamics of
the helicity-0 mode. The coupling to matter occurs via the coupling 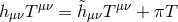 , where
, where 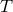 is
the trace of the external stress-energy tensor. We see that the helicity-0 mode couples directly to conserved
sources (unlike in the case of the Proca field) but the helicity-1 mode does not. In most of what follows we
will thus be able to ignore the helicity-1 mode.
is
the trace of the external stress-energy tensor. We see that the helicity-0 mode couples directly to conserved
sources (unlike in the case of the Proca field) but the helicity-1 mode does not. In most of what follows we
will thus be able to ignore the helicity-1 mode.
Higgs mechanism for gravity
As we shall see in Section 9.1, the graviton mass can also be promoted to a scalar function of one or many
other fields (for instance of a different scalar field), 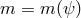 . We can thus wonder whether a dynamical
Higgs mechanism for gravity can be considered where the field(s)
. We can thus wonder whether a dynamical
Higgs mechanism for gravity can be considered where the field(s) 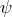 start in a phase for which the
graviton mass vanishes,
start in a phase for which the
graviton mass vanishes, 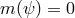 and dynamically evolves to acquire a non-vanishing vev for which
and dynamically evolves to acquire a non-vanishing vev for which
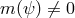 . Following the same logic as the Abelian Higgs for electromagnetism, this strategy can only
work if the number of dofs in the massless phase
. Following the same logic as the Abelian Higgs for electromagnetism, this strategy can only
work if the number of dofs in the massless phase 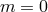 is the same as that in the massive case
is the same as that in the massive case
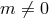 . Simply promoting the mass to a function of an external field is thus not sufficient
since the graviton helicity-0 and -1 modes would otherwise be infinitely strongly coupled as
. Simply promoting the mass to a function of an external field is thus not sufficient
since the graviton helicity-0 and -1 modes would otherwise be infinitely strongly coupled as
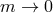 .
.
To date no candidate has been proposed for which the graviton mass could dynamically evolve from a vanishing value to a finite one without falling into such strong coupling issues. This does not imply that Higgs mechanism for gravity does not exist, but as yet has not been found. For instance on AdS, there could be a Higgs mechanism as proposed in [431], where the mass term comes from integrating out some conformal fields with slightly unusual (but not unphysical) ‘transparent’ boundary conditions. This mechanism is specific to AdS and to the existence of time-like boundary and would not apply on Minkowski or dS.
2.2.3 Van Dam–Veltman–Zakharov discontinuity
As in the case of spin-1, the massive spin-2 field propagates more dofs than the massless one. Nevertheless,
these new excitations bear no observational signatures for the spin-1 field when considering an arbitrarily
small mass, as seen in Section 2.1.2. The main reason for that is that the helicity-0 polarization of the
photon couple only to the divergence of external sources which vanishes for conserved sources. As a result
no external sources directly excite the helicity-0 mode of a massive spin-1 field. For the spin-2
field, on the other hand, the situation is different as the helicity-0 mode can now couple to the
trace of the stress-energy tensor and so generic sources will excite not only the 2 helicity-2
polarization of the graviton but also a third helicity-0 polarization, which could in principle have
dramatic consequences. To see this more explicitly, let us compute the gravitational exchange
amplitude between two sources 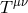 and
and 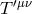 in both the massive and massless gravitational
cases.
in both the massive and massless gravitational
cases.
In the massless case, the theory is diffeomorphism invariant. When considering coupling to external
sources, of the form 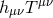 , we thus need to ensure that the symmetry be preserved, which implies that
the stress-energy tensor
, we thus need to ensure that the symmetry be preserved, which implies that
the stress-energy tensor 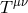 should be conserved
should be conserved 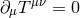 . When computing the gravitational
exchange amplitude between two sources we thus restrict ourselves to conserved ones. In the massive case,
there is a priori no reasons to restrict ourselves to conserved sources, so long as their divergences cancel in
the massless limit
. When computing the gravitational
exchange amplitude between two sources we thus restrict ourselves to conserved ones. In the massive case,
there is a priori no reasons to restrict ourselves to conserved sources, so long as their divergences cancel in
the massless limit 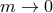 .
.
Massive spin-2 field
Let us start with the massive case, and consider the response to a conserved external source 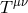 ,
,
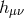 we consider the trace and the divergence
separately,
As is already apparent at this level, the massless limit
we consider the trace and the divergence
separately,
As is already apparent at this level, the massless limit 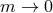 is not smooth which is at the origin of the
vDVZ discontinuity (for instance we see immediately that for a conserved source the linearized Ricci scalar
vanishes
is not smooth which is at the origin of the
vDVZ discontinuity (for instance we see immediately that for a conserved source the linearized Ricci scalar
vanishes  see Refs. [465*, 497*]. This linearized vDVZ discontinuity was recently
repointed out in [193].) As has been known for many decades, this discontinuity (or the fact that the Ricci
scalar vanishes) is an artefact of the linearized theory and is resolved by the Vainshtein mechanism [463*] as
we shall see later.
see Refs. [465*, 497*]. This linearized vDVZ discontinuity was recently
repointed out in [193].) As has been known for many decades, this discontinuity (or the fact that the Ricci
scalar vanishes) is an artefact of the linearized theory and is resolved by the Vainshtein mechanism [463*] as
we shall see later.
Plugging these expressions back into the modified Einstein equation, we get
with The propagator for a massive spin-2 field is thus given by where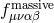 is the polarization tensor,
In Fourier space we have
The amplitude exchanged between two sources
is the polarization tensor,
In Fourier space we have
The amplitude exchanged between two sources 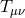 and
and 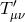 via a massive spin-2 field is thus given by
As mentioned previously, to compare this result with the massless case, the sources ought to be conserved in
the massless limit,
via a massive spin-2 field is thus given by
As mentioned previously, to compare this result with the massless case, the sources ought to be conserved in
the massless limit, 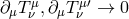 as
as 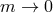 . The gravitational exchange amplitude in the massless
limit is thus given by
We now compare this result with the amplitude exchanged by a purely massless graviton.
. The gravitational exchange amplitude in the massless
limit is thus given by
We now compare this result with the amplitude exchanged by a purely massless graviton.
Massless spin-2 field
In the massless case, the equation of motion (2.50*) reduces to the linearized Einstein equation
where diffeomorphism invariance requires the stress-energy to be conserved,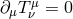 . In this
case the transverse part of this equation is trivially satisfied (as a consequence of the Bianchi
identity which follows from symmetry). Since the theory is invariant under diffeomorphism
transformations (2.38*), one can choose a gauge of our choice, for instance de Donder (or harmonic) gauge
In de Donder gauge, the Einstein equation then reduces to
The propagator for a massless spin-2 field is thus given by
where
. In this
case the transverse part of this equation is trivially satisfied (as a consequence of the Bianchi
identity which follows from symmetry). Since the theory is invariant under diffeomorphism
transformations (2.38*), one can choose a gauge of our choice, for instance de Donder (or harmonic) gauge
In de Donder gauge, the Einstein equation then reduces to
The propagator for a massless spin-2 field is thus given by
where 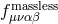 is the polarization tensor,
The amplitude exchanged between two sources
is the polarization tensor,
The amplitude exchanged between two sources 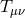 and
and 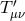 via a genuinely massless spin-2 field is thus
given by
and differs from the result (2.60*) in the small mass limit. This difference between the massless limit of the
massive propagator and the massless propagator (and gravitational exchange amplitude) is a well-known
fact and was first pointed out by van Dam, Veltman and Zakharov in 1970 [465, 497]. The resolution to
this ‘problem’ lies within the Vainshtein mechanism [463]. In 1972, Vainshtein showed that a theory of
massive gravity becomes strongly coupled a low energy scale when the graviton mass is small. As a result,
the linear theory is no longer appropriate to describe the theory in the limit of small mass and one should
keep track of the non-linear interactions (very much as what we do when approaching the Schwarzschild
radius in GR.) We shall see in Section 10.1 how a special set of interactions dominate in the massless
limit and are responsible for the screening of the extra degrees of freedom present in massive
gravity.
via a genuinely massless spin-2 field is thus
given by
and differs from the result (2.60*) in the small mass limit. This difference between the massless limit of the
massive propagator and the massless propagator (and gravitational exchange amplitude) is a well-known
fact and was first pointed out by van Dam, Veltman and Zakharov in 1970 [465, 497]. The resolution to
this ‘problem’ lies within the Vainshtein mechanism [463]. In 1972, Vainshtein showed that a theory of
massive gravity becomes strongly coupled a low energy scale when the graviton mass is small. As a result,
the linear theory is no longer appropriate to describe the theory in the limit of small mass and one should
keep track of the non-linear interactions (very much as what we do when approaching the Schwarzschild
radius in GR.) We shall see in Section 10.1 how a special set of interactions dominate in the massless
limit and are responsible for the screening of the extra degrees of freedom present in massive
gravity.
Another ‘non-GR’ effect was also recently pointed out in Ref. [280] where a linear analysis showed that massive gravity predicts different spin-orientations for spinning objects.
2.3 From linearized diffeomorphism to full diffeomorphism invariance
When considering the massless and non-interactive spin-2 field in Section 2.2.1, the linear gauge
invariance (2.38*) is exact. However, if this field is to be probed and communicates with the rest of the
world, the gauge symmetry is forced to include non-linear terms which in turn forces the kinetic term to
become fully non-linear. The result is the well-known fully covariant Einstein–Hilbert term 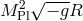 ,
where
,
where 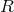 is the scalar curvature associated with the metric
is the scalar curvature associated with the metric 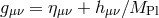 .
.
To see this explicitly, let us start with the linearized theory and couple it to an external source 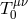 ,
via the coupling
,
via the coupling
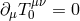 . To be more
explicit, let us consider a massless scalar field
. To be more
explicit, let us consider a massless scalar field 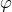 which satisfies the Klein–Gordon equation
which satisfies the Klein–Gordon equation 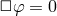 . A
natural choice for the stress-energy tensor
. A
natural choice for the stress-energy tensor 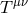 is then
so that the Klein–Gordon equation automatically guarantees the conservation of the stress-energy tensor
on-shell at the linear level and linearized diffeomorphism invariance. However, the very coupling between
the scalar field and the spin-2 field affects the Klein–Gordon equation in such a way that beyond the
linear order, the stress-energy tensor given in (2.68*) fails to be conserved. When considering the
coupling (2.67*), the Klein–Gordon equation receives corrections of the order of
is then
so that the Klein–Gordon equation automatically guarantees the conservation of the stress-energy tensor
on-shell at the linear level and linearized diffeomorphism invariance. However, the very coupling between
the scalar field and the spin-2 field affects the Klein–Gordon equation in such a way that beyond the
linear order, the stress-energy tensor given in (2.68*) fails to be conserved. When considering the
coupling (2.67*), the Klein–Gordon equation receives corrections of the order of 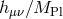 implying a failure of conservation of
implying a failure of conservation of 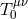 at the same order,
The resolution is of course to include non-linear corrections in
at the same order,
The resolution is of course to include non-linear corrections in 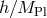 in the coupling with external
matter,
and promote diffeomorphism invariance to a non-linearly realized gauge symmetry, symbolically,
so this gauge invariance is automatically satisfied on-shell order by order in
in the coupling with external
matter,
and promote diffeomorphism invariance to a non-linearly realized gauge symmetry, symbolically,
so this gauge invariance is automatically satisfied on-shell order by order in 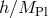 , i.e., the
scalar field (or general matter field) equations of motion automatically imply the appropriate
relation for the stress-energy tensor to all orders in
, i.e., the
scalar field (or general matter field) equations of motion automatically imply the appropriate
relation for the stress-energy tensor to all orders in 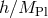 . The resulting symmetry is the
well-known fully non-linear coordinate transformation invariance (or full diffeomorphism invariance or
covariance4),
which requires the stress-energy tensor to be covariantly conserved. To satisfy this symmetry, the kinetic
term (2.36*) should then be promoted to a fully non-linear contribution,
Just as the linearized version
. The resulting symmetry is the
well-known fully non-linear coordinate transformation invariance (or full diffeomorphism invariance or
covariance4),
which requires the stress-energy tensor to be covariantly conserved. To satisfy this symmetry, the kinetic
term (2.36*) should then be promoted to a fully non-linear contribution,
Just as the linearized version 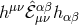 was unique, the non-linear realization
was unique, the non-linear realization 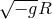 is also
unique.5
As a result, any theory of an interacting spin-2 field is necessarily fully non-linear and leads to the theory of
gravity where non-linear diffeomorphism invariance (or covariance) plays the role of the local gauge
symmetry that projects out four out of the potential six degrees of freedom of the graviton and prevents the
excitation of any ghost by the kinetic term.
is also
unique.5
As a result, any theory of an interacting spin-2 field is necessarily fully non-linear and leads to the theory of
gravity where non-linear diffeomorphism invariance (or covariance) plays the role of the local gauge
symmetry that projects out four out of the potential six degrees of freedom of the graviton and prevents the
excitation of any ghost by the kinetic term.
The situation is very different from that of a spin-1 field as seen earlier, where coupling with other fields
can be implemented at the linear order without affecting the 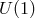 gauge symmetry. The difference is that
in the case of a
gauge symmetry. The difference is that
in the case of a 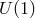 symmetry, there is a unique nonlinear completion of that symmetry, i.e., the unique
nonlinear completion of a
symmetry, there is a unique nonlinear completion of that symmetry, i.e., the unique
nonlinear completion of a 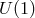 is nothing else but a
is nothing else but a 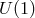 . Thus any nonlinear Lagrangian which
preserves the full
. Thus any nonlinear Lagrangian which
preserves the full 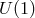 symmetry will be a consistent interacting theory. On the other hand, for spin-2
fields, there are two, and only two ways to nonlinearly complete linear diffs, one as linear diffs in the full
theory and the other as full non-linear diffs. While it is possible to write self-interactions which preserve
linear diffs, there are no interactions between matter and
symmetry will be a consistent interacting theory. On the other hand, for spin-2
fields, there are two, and only two ways to nonlinearly complete linear diffs, one as linear diffs in the full
theory and the other as full non-linear diffs. While it is possible to write self-interactions which preserve
linear diffs, there are no interactions between matter and 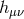 which preserve linear diffs. Thus
any theory of gravity must exhibit full nonlinear diffs and is in this sense what leads us to
GR.
which preserve linear diffs. Thus
any theory of gravity must exhibit full nonlinear diffs and is in this sense what leads us to
GR.
2.4 Non-linear Stückelberg decomposition
On the need for a reference metric
We have introduced the spin-2 field 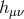 as the perturbation about flat spacetime. When considering the
theory of a field of given spin it is only natural to work with Minkowski as our spacetime metric, since
the notion of spin follows from that of Poincaré invariance. Now when extending the theory
non-linearly, we may also extend the theory about different reference metric. When dealing
with a reference metric different than Minkowski, one loses the interpretation of the field as
massive spin-2, but one can still get a consistent theory. One could also wonder whether it is
possible to write a theory of massive gravity without the use of a reference metric at all. This
interesting question was investigated in [75*], where it shown that the only consistent alternative is
to consider a function of the metric determinant. However, as shown in [75*], the consistent
function of the determinant is the cosmological constant and does not provide a mass for the
graviton.
as the perturbation about flat spacetime. When considering the
theory of a field of given spin it is only natural to work with Minkowski as our spacetime metric, since
the notion of spin follows from that of Poincaré invariance. Now when extending the theory
non-linearly, we may also extend the theory about different reference metric. When dealing
with a reference metric different than Minkowski, one loses the interpretation of the field as
massive spin-2, but one can still get a consistent theory. One could also wonder whether it is
possible to write a theory of massive gravity without the use of a reference metric at all. This
interesting question was investigated in [75*], where it shown that the only consistent alternative is
to consider a function of the metric determinant. However, as shown in [75*], the consistent
function of the determinant is the cosmological constant and does not provide a mass for the
graviton.
Non-linear Stückelberg
Full diffeomorphism invariance (or covariance) indicates that the theory should be built
out of scalar objects constructed out of the metric 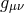 and other tensors. However,
as explained previously a theory of massive gravity requires the notion of a reference
metric6
and other tensors. However,
as explained previously a theory of massive gravity requires the notion of a reference
metric6
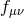 (which may be Minkowski
(which may be Minkowski 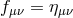 ) and at the linearized level, the mass for gravity was not built
out of the full metric
) and at the linearized level, the mass for gravity was not built
out of the full metric 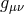 , but rather out of the fluctuation
, but rather out of the fluctuation 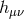 about this reference metric which does
not transform as a tensor under general coordinate transformations. As a result the mass term breaks
covariance.
about this reference metric which does
not transform as a tensor under general coordinate transformations. As a result the mass term breaks
covariance.
This result is already transparent at the linear level where the mass term (2.39*) breaks linearized diffeomorphism invariance. Nevertheless, that gauge symmetry can always be ‘formally’ restored using the Stückelberg trick which amounts to replacing the reference metric (so far we have been working with the flat Minkowski metric as the reference), to
and transforming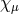 under linearized diffeomorphism in such a way that the combination
under linearized diffeomorphism in such a way that the combination 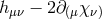 remains invariant. Now that the symmetry is non-linearly realized and replaced by general covariance, this
Stückelberg trick should also be promoted to a fully covariant realization.
remains invariant. Now that the symmetry is non-linearly realized and replaced by general covariance, this
Stückelberg trick should also be promoted to a fully covariant realization.
Following the same Stückelberg trick non-linearly, one can ‘formally restore’ covariance by including
four Stückelberg fields 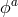 (
(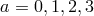 ) and promoting the reference metric
) and promoting the reference metric 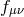 , which may of may
not be Minkowski, to a tensor
, which may of may
not be Minkowski, to a tensor 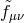 [446*, 27*],
[446*, 27*],
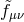 transforms as a tensor under coordinate transformations as
long as each of the four fields
transforms as a tensor under coordinate transformations as
long as each of the four fields 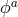 transform as scalars. We may now construct the theory of massive
gravity as a scalar Lagrangian of the tensors
transform as scalars. We may now construct the theory of massive
gravity as a scalar Lagrangian of the tensors 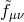 and
and 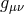 . In unitary gauge, where the Stückelberg
fields are
. In unitary gauge, where the Stückelberg
fields are 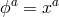 , we simply recover
, we simply recover 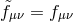 .
.
This Stückelberg trick for massive gravity dates already from Green and Thorn [267] and from Siegel [446], introduced then within the context of open string theory. In the same way as the massless graviton naturally emerges in the closed string sector, open strings also have spin-2 excitations but whose lowest energy state is massive at tree level (they only become massless once quantum corrections are considered). Thus at the classical level, open strings contain a description of massive excitations of a spin-2 field, where gauge invariance is restored thanks to same Stückelberg fields as introduced in this section. In open string theory, these Stückelberg fields naturally arise from the ghost coordinates. When constructing the non-linear theory of massive gravity from extra dimension, we shall see that in that context the Stückelberg fields naturally arise at the shift from the extra dimension.
For later convenience, it will be useful to construct the following tensor quantity,
in unitary gauge,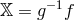 .
.
Alternative Stückelberg trick
An alternative way to Stückelberize the reference metric 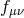 is to express it as
is to express it as
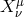 and
and 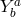 have the same eigenvalues, so one can
choose either one of them in the definition of the massive gravity Lagrangian without any distinction.
The formulation in terms of
have the same eigenvalues, so one can
choose either one of them in the definition of the massive gravity Lagrangian without any distinction.
The formulation in terms of 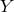 rather than
rather than 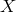 was originally used in Ref. [94], although
unsuccessfully as the potential proposed there exhibits the BD ghost instability, (see for instance
Ref. [60]).
was originally used in Ref. [94], although
unsuccessfully as the potential proposed there exhibits the BD ghost instability, (see for instance
Ref. [60]).
Helicity decomposition
If we now focus on the flat reference metric, 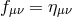 , we may further split the
Stückelberg fields as
, we may further split the
Stückelberg fields as 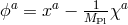 and identify the index
and identify the index  with a Lorentz
index,7
we obtain the non-linear generalization of the Stückelberg trick used in Section 2.2.2
with a Lorentz
index,7
we obtain the non-linear generalization of the Stückelberg trick used in Section 2.2.2
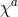 in terms of the helicity-0
and -1 modes and all indices are raised and lowered with respect to
in terms of the helicity-0
and -1 modes and all indices are raised and lowered with respect to 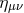 .
.
In other words, the fluctuations about flat spacetime are promoted to the tensor 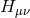
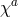 are introduced to restore the gauge invariance (full diffeomorphism invariance). We can now
always set a gauge where
are introduced to restore the gauge invariance (full diffeomorphism invariance). We can now
always set a gauge where 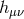 is transverse and traceless at the linearized level and
is transverse and traceless at the linearized level and 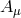 is
transverse. In this gauge the quantities
is
transverse. In this gauge the quantities 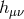 ,
, 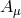 and
and 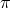 represent the helicity decomposition
of the metric.
represent the helicity decomposition
of the metric. 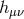 is the helicity-2 part of the graviton,
is the helicity-2 part of the graviton, 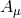 the helicity-1 part and
the helicity-1 part and 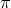 the helicity-0 part. The fact that these quantities continue to correctly identify the physical
degrees of freedom non-linearly in the limit
the helicity-0 part. The fact that these quantities continue to correctly identify the physical
degrees of freedom non-linearly in the limit 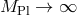 is non-trivial and has been derived
in [143*].
is non-trivial and has been derived
in [143*].
Non-linear Fierz–Pauli
The most straightforward non-linear extension of the Fierz–Pauli mass term is as follows
this mass term is then invariant under non-linear coordinate transformations. This non-linear formulation was used for instance in [27]. Alternatively, one may also generalize the Fierz–Pauli mass non-linearly as follows [75*] A priori, the linear Fierz–Pauli action for massive gravity can be extended non-linearly in an arbitrary number of ways. However, as we shall see below, most of these generalizations generate a ghost non-linearly, known as the Boulware–Deser (BD) ghost. In Part II, we shall see that the extension of the Fierz–Pauli to a non-linear theory free of the BD ghost is unique (up to two constant parameters).
2.5 Boulware–Deser ghost
The easiest way to see the appearance of a ghost at the non-linear level is to follow the Stückelberg trick
non-linearly and observe the appearance of an Ostrogradsky instability [111*, 173*], although the
original formulation was performed in unitary gauge in [75*] in the ADM language (Arnowitt,
Deser and Misner, see Ref. [29]). In this section we shall focus on the flat reference metric,
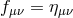 .
.
Focusing solely on the helicity-0 mode 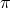 to start with, the tensor
to start with, the tensor 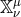 defined in (2.76*) is expressed
as
defined in (2.76*) is expressed
as
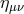 . Then
the Fierz–Pauli mass term (2.83*) reads
Upon integration by parts, we notice that the quadratic term in (2.86*) is a total derivative, which is
another way to see the special structure of the Fierz–Pauli mass term. Unfortunately this special fact does
not propagate to higher order and the cubic and quartic interactions are genuine higher order
operators which lead to equations of motion with quartic and cubic derivatives. In other words
these higher order operators
. Then
the Fierz–Pauli mass term (2.83*) reads
Upon integration by parts, we notice that the quadratic term in (2.86*) is a total derivative, which is
another way to see the special structure of the Fierz–Pauli mass term. Unfortunately this special fact does
not propagate to higher order and the cubic and quartic interactions are genuine higher order
operators which lead to equations of motion with quartic and cubic derivatives. In other words
these higher order operators ![([Π3 ] − [Π ][Π2])](article354x.gif) and
and ![([Π4] − [Π2 ]2)](article355x.gif) propagate an additional
degree of freedom which by Ostrogradsky’s theorem, always enters as a ghost. While at the
linear level, these operators might be irrelevant, their existence implies that one can always
find an appropriate background configuration
propagate an additional
degree of freedom which by Ostrogradsky’s theorem, always enters as a ghost. While at the
linear level, these operators might be irrelevant, their existence implies that one can always
find an appropriate background configuration 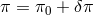 , such that the ghost is manifest
with
, such that the ghost is manifest
with 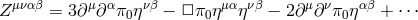 . This implies that non-linearly (or around a
non-trivial background), the Fierz–Pauli mass term propagates an additional degree of freedom which is a
ghost, namely the BD ghost. The mass of this ghost depends on the background configuration
. This implies that non-linearly (or around a
non-trivial background), the Fierz–Pauli mass term propagates an additional degree of freedom which is a
ghost, namely the BD ghost. The mass of this ghost depends on the background configuration 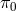 ,
As we shall see below, the resolution of the vDVZ discontinuity lies in the Vainshtein mechanism for which
the field takes a large vacuum expectation value,
,
As we shall see below, the resolution of the vDVZ discontinuity lies in the Vainshtein mechanism for which
the field takes a large vacuum expectation value, 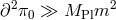 , which in the present context would lead
to a ghost with an extremely low mass,
, which in the present context would lead
to a ghost with an extremely low mass, 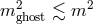 .
.
Choosing another non-linear extension for the Fierz–Pauli mass term as in (2.84*) does not seem to help much,
where we have integrated by parts on the second line, and we recover exactly the same type of higher derivatives already at the cubic level, so the BD ghost is also present in (2.84*).Alternatively the mass term was also generalized to include curvature invariants as in Ref. [69]. This theory was shown to be ghost-free at the linear level on FLRW but not yet non-linearly.
Function of the Fierz–Pauli mass term
As an extension of the Fierz–Pauli mass term, one could instead write a more general function of it, as considered in Ref. [75*]
however, one can easily see, if a mass term is actually present, i.e.,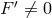 , there is no analytic choice of
the function
, there is no analytic choice of
the function 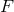 which would circumvent the non-linear propagation of the BD ghost. Expanding
which would circumvent the non-linear propagation of the BD ghost. Expanding 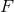 into
a Taylor expansion, we see for instance that the only choice to prevent the cubic higher-derivative
interactions in
into
a Taylor expansion, we see for instance that the only choice to prevent the cubic higher-derivative
interactions in 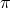 ,
, ![[Π3] − [Π ][Π2 ]](article369x.gif) is
is 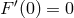 , which removes the mass term at the same time. If
, which removes the mass term at the same time. If
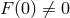 but
but 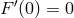 , the theory is massless about the specific reference metric, but infinitely
strongly coupled about other backgrounds.
, the theory is massless about the specific reference metric, but infinitely
strongly coupled about other backgrounds.
Instead to prevent the presence of the BD ghost fully non-linearly (or equivalently about any
background), one should construct the mass term (or rather potential term) in such a way, that all the
higher derivative operators involving the helicity-0 mode 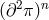 are total derivatives. This is precisely
what is achieved in the “ghost-free” model of massive gravity presented in Part II. In the next Part I we
shall use higher dimensional GR to get some insight and intuition on how to construct a consistent theory
of massive gravity.
are total derivatives. This is precisely
what is achieved in the “ghost-free” model of massive gravity presented in Part II. In the next Part I we
shall use higher dimensional GR to get some insight and intuition on how to construct a consistent theory
of massive gravity.

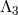 -decoupling
limit of bi-gravity
-decoupling
limit of bi-gravity
 )
)

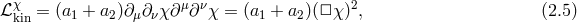






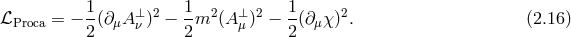


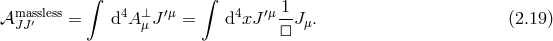
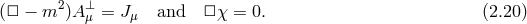
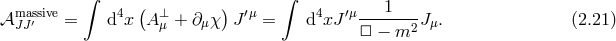
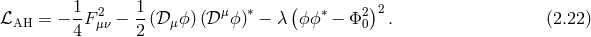

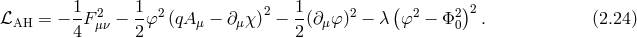
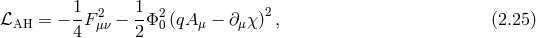





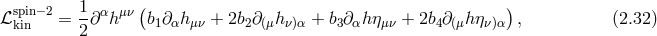

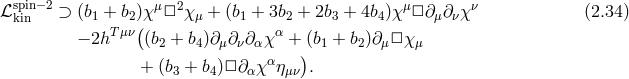

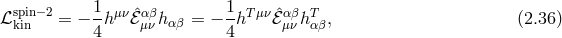
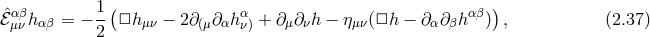


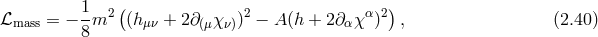

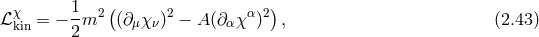
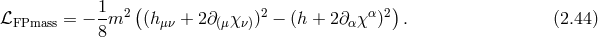


![1- μν ˆαβ 1- μν 1- 2 ℒFP = − 4 h ℰμν h αβ − 2h (Πμν − [Π]ημν) − 8F μν (2.47 ) 1 ( ) 1 − --m2 h2μν − h2 − --m (hμν − hημν) ∂(μA ν), 8 2](article213x.gif)
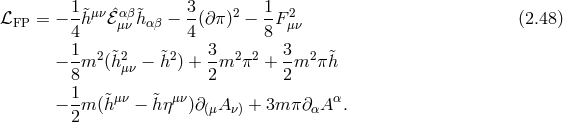
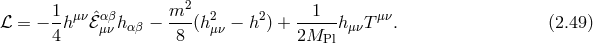
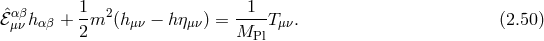
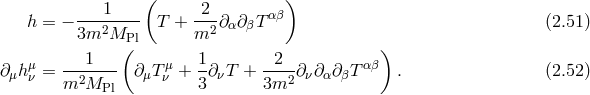
![( ) 1 [ 1 2 1 □ − m2 hμν = − ---- T μν − -T ημν − --2∂(μ∂αTνα) + ---2∂μ∂ νT (2.53 ) MPl 3 m 3m ] + --1- ∂ ∂ T αβη + -2--∂ ∂ ∂ ∂ T αβ 3m2 α β μν 3m4 μ ν α β 1 [ 1 ] = ---- &tidle;ημ(αη&tidle;νβ) − -η&tidle;μν&tidle;ηαβ Tα β, (2.54 ) MPl 3](article246x.gif)



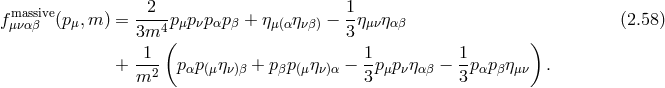
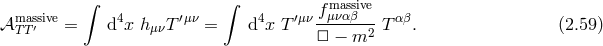
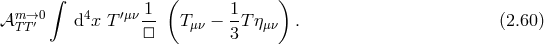


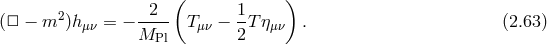


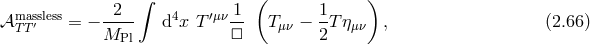


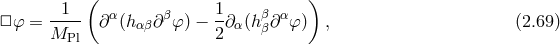
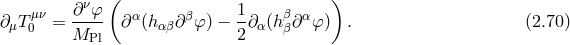
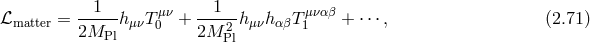
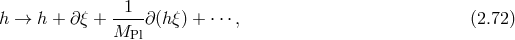
![spin−2 1 spin−2 M 2 √ --- ℒkin linear = − -h μν ˆℰαμβν h αβ −→ ℒkin covariant = --Pl − gR[g]. (2.73 ) 4 2](article287x.gif)




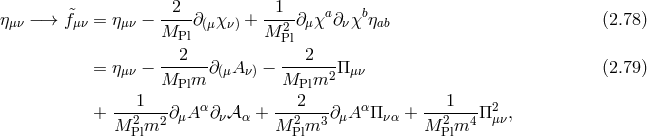
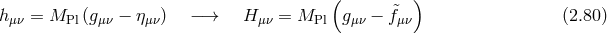
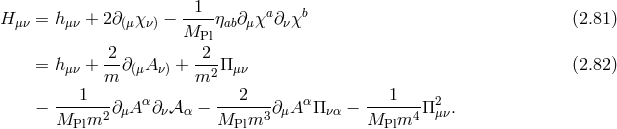
![√ ---( ) ℒ(nl1)= − m2M 2Pl − g [(𝕀 − 𝕏)2] − [𝕀 − 𝕏]2 , (2.83 ) FP](article346x.gif)
![ℒ (nl2)= − m2M 2 √ − g-√det-𝕏-([(𝕀 − 𝕏 −1)2] − [𝕀 − 𝕏 −1]2). (2.84 ) FP Pl](article347x.gif)
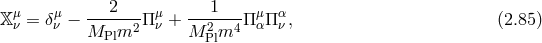
![( ) ( ) ( ) ℒ(nl1) = − -4- [Π2 ] − [Π]2 + ---4--- [Π3] − [Π][Π2 ] + --1---- [Π4] − [Π2 ]2 . (2.86 ) FP,π m2 MPlm4 M 2Plm6](article353x.gif)
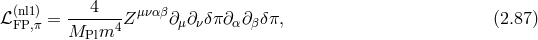

![ℒ (nl2) = − -4-([Π2 ] − [Π]2) −---4---([Π ]3 − 4[Π][Π2 ] + 3 [Π3 ]) + ⋅⋅⋅ FP,π m2 MPlm4 4 ( 2 3 ) → ------4 [Π ][Π ] − [Π ] + ⋅⋅⋅ (2.89 ) MPlm](article363x.gif)