The prior distributions as initially specified were very flat in the hyperparameters.
Closer examination of the situation revealed an experience which is well known, that
of specifying priors for parameters, where the true parameter of interest is in fact a
transformed variable. For this model, it was desired to specify a prior distribution
for the hyperparameters, 
, which were related to the logit of the
proportion of interest, p. Graphically, this observation is shown in
Figure 
. A central prior for logit(p) translates as a flat prior for
p. Very slight difference in location has a noticeable affect on the distribution of
p. In fact, a moderately high precision on logit(p) turns out to yield a not too
precise prior for p.
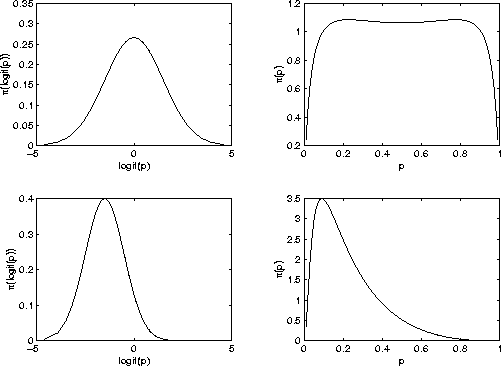
Figure: Reason for care in prior
specification when transforming variable.
In fact, a certain amount was known about p. It was known that p would not be
likely to exceed 0.5, and would probably be smaller than that. With the limited amount
of observation, this knowledge should certainly be incorporated in any specification
of the prior. The prior for 
was specified as normal with mean -0.5 and
variance 
and for 
as normal with mean 
and
precision 
, where 
was the average time of observation.