A very basic model was used for the coalescence. It was decided to
model the rate of coalescence directly. The actual spatial
mechanism itself can only be addressed at a later date in the
light of spatial data. The rate of coalescence is modelled using a
binomial model, with non-constant p as a function of time. The
directed graph of this model is shown in Figure 
.
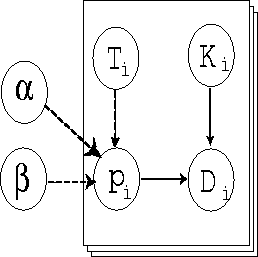
Figure: DAG for Model of
Coalescence
The observed number of coalescences at the 
stage is 
, and is taken to be
binomial. The number of cracks available for coalescence is 
, and 
is the
proportion coalescing.
The time of the observation is 
. The proportion, is assumed to
be such that
logit( ) depends linearly on time, that is
.
A model
for coalescence was programmed in WinBugs [51]. The directed acyclic
graph associated with the model is shown in Figure . Convergence was
assessed by visual examination of the chains, and the normal estimates provided from
the monitored variables.