The combination of the growth and coalescence models yields some useful results. The
posterior distributions of the 
are interesting, in that they demonstrate that
the total crack length after coalescence is often substantially less than the sum of
the lengths of the constituent cracks before coalescence. The posterior distribution
of the 
does not differ substantially from the prior. This is likely to be due to
the fact that is confounded with , since the new crack grows from time of
coalescence, a shorter original length will be sampled for an earlier time within the
interval and vice-versa. The posterior for the parameters obtained for the growth only
model, assumed that there was no coalescence. As such the data was not pure growth,
but was rather transformed data. The fact that the joint model separates out the
growth effect from the coalescence effect allows a more correct consideration of the
data. Cracks which have been involved in coalescence are observed at fewer times,
however, so there is less data with which to make accurate estimates of the crack
specific parameters.
For computational reasons, and since spatial data are not available, the reliability
has not been calculated for this case. However, the reliability of the specimen under
this model could, in principle, be estimated, since R(N) is a calculation based upon
the crack specific parameters and depends on the order of future coalescences, and
which crack coalesces with which. For example, in the case of 10 cracks, let 
denote the 
crack. One possible future ordering would be 
coalesces
with 
forming 
, then 
with 
forming 
then with
, and so on until there is only one crack left. This is only one possible
sequence of coalescence. Let o be a particular coalescence event, and let 
be
the set of all possible future coalescences. Then is finite, albeit very large
indeed. For example, for a set of 10 cracks, 
. Then;
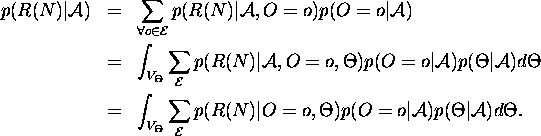
And recall that;
where the dependence on O determines which crack coalesces with which. The
depends upon the spatial distribution of the cracks. Any information on
the location of the cracks is useful in determining this; for example if the data were
observed in a number of different regions, it is likely that is close to
zero when O=o consists of coalescences of cracks in distinct regions.
A natural extension to the model is the case where the microcrack density (which is a
recognised damage function in the literature) is recorded for a number of different
regions. Following a similar methodology to [29] it is natural to extend
the hierarchical model, by having a rate 
specific to each region, with an
overall rate 
.
Thus the proposed joint model constitutes an attempt at modelling the two distinct effects; coalescence and growth. It is a flexible model which may be adapted to the case where spatial data is available.