On Quaternions; or on a new System of Imaginaries in Algebra. By SIR WILLIAM ROWAN HAMILTON LL.D, P.R.I.A., F.R.A.S., Hon. M. R. Soc. Ed. and Dub., Hon. or Corr. M. of the Royal or Imperial Academies of St. Petersburgh, Berlin, Turin and Paris, Member of the American Academy of Arts and Sciences, and of other Scientific Societies at Home and Abroad, Andrews' Prof. of Astronomy in the University of Dublin, and Royal Astronomer of Ireland.

[The London, Edinburgh and Dublin Philosophical Magazine and Journal of Science vol. xxv (1844), pp. 489-95]

To the Editors of the Philosophical Magazine and Journal

GENTLEMEN,

I have been induced to think that the account contained in the following letter, of the considerations which led me to conceive that theory of quaternions, a part of which you have done me the honour to publish in two recent Numbers (for July and October) of your Magazine, might not be without interest to some of your readers. Should you think proper to insert it, a public acknowledgement (very pleasing to my own feelings) will have been rendered, on the one hand to the Rev. Mr. Warren, whose work on the Geometrical Representation of the Square Roots of Negative Quantities (printed at Cambridge in 1828) long since attracted my attention and influenced my thoughts; and on the other hand to the gentleman (John T. Graves, Esq.) to whom the letter was addressed, and with whom I had been engaged, at intervals, for many years in a correspondence, very instructive and suggestive to me, on subjects connected therewith. Nor am I without hope that Mr. Graves may thus be led to communicate through you to mathematicians some of the extensions which he has made of results of mine, with some of those other speculations which are still more fully his own. On some future occasion I may perhaps be allowed to mention any other quarters from which I may be conscious of having derived more recent assistance, in my investigations on the same mathematical subject, many of which are hitherto unpublished.

I have the honour to be, Gentlemen,
Your obedient Servant,
WILLIAM ROWAN HAMILTON

Observatory of Trinity College, Dublin,
November 20, 1844

(Copy of a) Letter from Sir William R. Hamilton to John T. Graves, Esq. on Quaternions

Observatory, October 17, 1843

MY DEAR GRAVES,--A very curious train of mathematical speculation occurred to me yesterday, which I cannot but hope will prove of interest to you. You know that I have long wished, and I believe that you have felt the same desire, to possess a Theory of Triplets, analogous to my published Theory of Couplets, and also to Mr. Warren's geometrical representation of imaginary quantities. Now I think that I discovered¹ yesterday a theory of quaternions which includes such a theory of triplets.²

My train of thoughts was of this kind. Since is in a certain well-known sense, a line perpendicular to the line 1, it seemed natural that there should be some other imaginary to express a line perpendicular to the former; and because the rotation from this to this also being doubled conducts to -1, it ought also to be a square root of negative unity, though not to be confounded with the former. Calling the old root, as the Germans often do, i, and the new one j, I inquired what laws ought to be assumed for multiplying together a + ib + jc and x + iy + jz. It was natural to assume that the product

but what are we to do with ij? Shall it be of the form ? Its square would seem to be = 1, because ; and this might tempt us to take ij = 1 or ij = -1; but with neither assumption shall we have the sum of the squares of the coefficients of 1, i, and j in the product = to the product of the corresponding sums of squares in the factors. Take the simplest case of a product, namely, the case where it becomes a square; we have and ; the condition respecting the moduli is fulfilled, if we suppress the term involving ij altogether, and what is more , 2ab, 2ac are precisely the coordinates of the square-point, so to speak, deduced from the point a, b, c, in space, by a slight extension of Mr. Warren's rule for points in a plane. [It is a long time since I read this book, but the grand features of his view cannot be forgotten.] In fact, if we double, in its own plane, the rotation from the positive semiaxis of x to the radius vector of the point a, b, c, we attain the direction of the radius vector drawn to , 2ab, 2ac.

Behold me therefore tempted for a moment to fancy that ij = 0. But this seemed odd and uncomfortable, and I perceived that the same suppression of the term which was de trop might be attained by assuming what seemed to me less harsh, namely that ji = - ij. I made therefore ij = k, ji = -k, reserving to myself to inquire whether k was =0 or not. For this purpose, I next multiplied a + ib + jc, as a multiplier, into x + ib + jc, as a multiplicand, keeping still, as you see, the two factor lines in one common plane with the unit line. The result was

in which the coefficient of k still vanishes; and , (a + x)b, (a + x)c are easily found to be the correct coordinates of the product-point, in the sense that the rotation from the unit line to the radius vector of a, b, c, being added in its own plane to the rotation from the same unit-line to the radius vector of the other factor-point x, b, c, conducts to the radius vector of the lately mentioned product-point; and that this latter radius vector is in length the product of the two former. Confirmation of ij = - ji; but no information yet of the value of k. Try boldly then the general product of two triplets, and seek whether the law of the moduli is satisfied when we suppress the k altogether. Is

No, the first member exceeds the second by . But this is just the square of the coefficient of k, in the development of the product (a + ib + jc)(x + iy + jz), if we grant that ij = k, ji = -k, as before. And here there dawned on me the notion that we must admit, in some sense, a fourth dimension³ of space for the purpose of calculating with triplets; or transferring the paradox to algebra, must admit a third distinct imaginary symbol k, not to be confounded with either i or j, but equal to the product of the first as multiplier, and the second as multiplicand; and therefore was led to introduce quaternions, such as a + ib + jc + kd, or (a,b,c,d).

I saw that we had probably ik = -j, because ik = iij and ; and that in like manner we might expect to find kj = ijj = -i; from which I thought it likely that ki = j, jk = i, because it seemed likely that if ji = -ij, we should have also kj = - jk, ik = -ki. And since the order of multiplication of these imaginaries is not indifferent, we cannot infer that , or ijij, is +1, because . It is more likely that . And in fact this last assumption is necessary, if we would conform the multiplication of quaternions to the law of the multiplication of moduli. For multiplying a + ib + jc + kd as multiplier into a' + i b' + j c' + k d' as multiplicand, and granting that is real, we find for the real part of the product, ; and for the coefficient of k, ad' + da' + terms arising from the multiplication of i and j together; in order then that 2a a' d d' may disappear in the expression of the square of the modulus of the product, by being added to , it is necessary that we should have .

My assumptions were now completed, namely,

and with these I was obliged to assume that if

then the four following equations of multiplication hold good:

But I considered it essential to try whether these equations were consistent with the law of moduli, namely

without which consistence being verified, I should have regarded the whole speculation as a failure. Judge then of my pleasure when, after a careful examination, I found that the whole twenty-four products not involving squares in the development of the sum of the squares of the four quadrinomials (B.) destroyed each other; and that the sixteen products involving squares were just those which arise otherwise from the multiplication of and .⁴ We have, then, this first law for the multiplication of two quaternions together, that the modulus of the product is equal to the product of the moduli of the factors.

Division of quaternions is easy. The equations (B.) of multiplication give

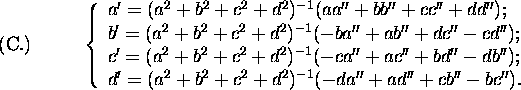
The modulus of the quotient is the quotient of the moduli. A quaternion divided by itself gives for quotient (1,0,0,0) = 1.

Addition and subtraction require no notice.

Making

I would call the amplitude of the quaternion, its colatitude; and its longitude. The modulus is . Representing the three coefficients b, c, d of the imaginary triplet ib + jc + kd, by the rectangular coordinates of a point in space; , as being the radius vector of this point, might be called the radius, or perhaps the length, of the quaternion. We may speak of the inclination of one quaternion to another, and its cosine is

If with the amplitudes , , of any two factors and their product, as sides, we construct a spherical triangle, the angle opposite to the amplitude of the product will be the supplement of the inclination of the factors to each other; and the angle opposite to the amplitude of either factor will be the inclination of the other factor to the product.⁵

This theorem of the spherical triangle, combined with the law of the moduli, requires only besides the following rule of rotation, to decide on which side of the plane of the two factor-lines the product-line is found, in order to complete the geometrical construction for the equations (B.) of multiplication of quaternions. In whichever direction, to the right or to the left, the positive semiaxis of i must rotate round that of k in order to approach to that of j; in the same direction must the multiplicand line turn round the multiplier-line in order to approach the product-line (or the plane containing the product-line and the multiplier-line).

If the factor-lines coincide with each other in direction, the product-line coincides with each of them; and its amplitude is the sum of theirs; because the spherical triangle degenerates into a single arc, two angles vanishing and the third becoming equal to two right angles. If the amplitudes of the factors are also supplementary to each other, the amplitude of the product is , and its sine vanishes; the product has therefore in this no length, or radius, but becomes a pure real, and at the same time a negative quantity; because , . The factors are in this case of the forms

and

and their product is

Making the factors equal, , we find that

The square of a pure imaginary is real and negative: the square root of a real negative is a pure imaginary, having a determined length, but a wholly undetermined direction. The square root of -1 is any one of the infinitely many pure imaginaries, of the form

In general, however, the square root of a quaternion has only two values, which differ only in sign: for if

then

and cannot vanish, except in the case of the pure negative square, b'' = c'' = d'' = 0, a'' < 0.

Multiplication will be easy if we are familiar with the rules for the product of two pure imaginaries. This product is, by (B.),

the product-line is perpendicular to the plane of the factors; its length is the product of their lengths multiplied by the sine of the angle between them: and the real part of the product, with its sign changed, is the same product of the lengths of the factors multiplied by the cosine of their inclination.

Finally we may always decompose the latter problem into these two others; to multiply two pure imaginaries which agree in direction, and to multiply two which are at right angles with each other. In the first case the product is a pure negative, equal to the product of the lengths or moduli with its sign changed. In the second case, the product is a pure imaginary of which the length is the product of the lengths of the factors, and which is perpendicular to both of them. The distinction between one such perpendicular and its opposite may be made by the rule of rotation already stated.

There seems to me to be something analogous to polarized intensity in the pure imaginary part; and to unpolarized energy (indifferent to direction) in the real part of a quaternion: and thus we have some slight glimpse of a future Calculus of Polarities. This is certainly very vague,⁶ but I hope that most of what I have said above is clear and mathematical. Hoping that you may be tempted to pursue the view which has thus opened, I remain, with best wishes,

Your sincere friend,
WILLIAM R. HAMILTON

Notes:

¹The reader is requested to pardon this expression for the reason mentioned in another note.

²Prof. De Morgan has most obligingly given the writer a sketch of a Memoir on Triple Algebra, which he has lately presented to the Cambridge Philosophical Society, and which he is pleased to say was not begun till after the publication of the first part of the paper on Quaternions in this Magazine.

³The writer has this moment been informed (in a letter from a friend) that in the Cambridge Mathematical Journal for May last a paper on Analytical Geometry of n dimensions has been published by Mr. Cayley, but regrets that he does not yet know how far Mr. Cayley's views and his own may resemble or differ from each other.

⁴Mr. Graves has since pointed out to the writer that this theorem of ordinary algebra is not new, and has very elegantly extended it.

⁵An improved form of this theorem of the spherical triangle was communicated by the writer to the Royal Irish Academy in November 1843, and has been published in the Philosophical Magazine for July 1844.

⁶A pen has been drawn across a clause or two in the foregoing copy of this letter, as having reference only to this guess of a future physical application. A postscript has also been suppressed, as being comparatively private. In other respects, it has been thought that no change ought to be made, if the letter were to be printed at all; and therefore the indulgence of the reader is requested for some expressions which have the air of attaching to the subject an importance greater than it may deserve.

Links:

• Hamilton's Research on Quaternions
• Sir William Rowan Hamilton (1805-1865)
• History of Mathematics