By WILLIAM R. HAMILTON, M.R.I.A., Royal Astronomer of Ireland.
[Report of the Third Meeting of the British Association for the Advancement of Science held at Cambridge in 1833 (John Murray, London, 1834), 360-370.]
The author gave a statement of some optical results, deduced from the view which he had explained in the preceding year at Oxford.
His general method, for the study of optical systems, consists in expressing the properties of any optical combination by the form of ONE CHARACTERISTIC FUNCTION, one central or radical relation. In order to investigate the properties of the systems of rays, produced by any object-glass, or atmosphere, or other optical instrument, or combination of surfaces and media, ordinary or extraordinary, he has proposed, as a fundamental problem, to express for any such combination, the laws of dependence of the final and initial directions of a linear path of light on the final and initial positions or points, and on the colour. And the solution which he has offered for this fundamental problem consists, 1st, in reducing by uniform methods (analogous to the methods of discussing the equation of a curve or surface,) these several laws of dependence (of the four extreme angles of direction of a curved or polygon ray on the six extreme coordinates and on the colour,) to that one law, different for different combinations, according to which his one characteristic function depends on the same seven variables. And 2ndly, in establishing uniform processes for the research of the form of this function, namely, the action or time of propagation of the light, for any proposed combination.
For example, in the case of a single plane mirror, supposed to
coincide with the plane of x y, we may propose to determine the
laws of the two extreme directions of the linear path by which light
goes to an eye (x y z) from an object (x' y' z'), or
(expressing the same thing more fully,) to determine the final cosines
![]()
![]()
![]() , and the initial cosines
, and the initial cosines ![]()
![]()
![]() , of the inclinations of this bent path to the positive
semiaxes of coordinates, as functions of x y z, x' y' z',
that is, of the six extreme coordinates themselves, the colour being
here indifferent. And Mr. Hamilton's general solution, for this and
for all other questions respecting combinations of ordinary
reflectors,--a solution which is itself a particular case of a more
general result, extending to all optical combinations,--is expressed
by the following equations:
, of the inclinations of this bent path to the positive
semiaxes of coordinates, as functions of x y z, x' y' z',
that is, of the six extreme coordinates themselves, the colour being
here indifferent. And Mr. Hamilton's general solution, for this and
for all other questions respecting combinations of ordinary
reflectors,--a solution which is itself a particular case of a more
general result, extending to all optical combinations,--is expressed
by the following equations:
the characteristic function V representing, in all questions respecting combinations of reflectors, the length of the bent path of the light, and being for the present mirror of the form
![]()
but being different in other cases. Thus, for a reflecting sphere, or
for a Newtonian telescope, the length of a bent path of light would depend
differently on the extreme points of that path, and we should have a
different form for the characteristic function V; but by
substituting this new form in the equations (1.), we should
still deduce the connected forms of the six direction-functions
or direction-cosines ![]()
![]()
![]() ,
, ![]()
![]()
![]() , and so might deduce all the other properties of the
telescope; at least, all the properties connected with its effects
upon systems of rays.
, and so might deduce all the other properties of the
telescope; at least, all the properties connected with its effects
upon systems of rays.
It may be perceived from what has been said, that Mr. Hamilton divides mathematical optics into two principal parts: one part proposing to find in every particular case the form of the characteristic function V, and the other part proposing to use it: as in algebraical geometry, it is one class of problems to determine the equations of curves or surfaces which satisfy assigned conditions; and it is another class of problems to discuss these equations when determined. The investigations which the author has printed in the fifteenth, sixteenth, and seventeenth volumes of the Transactions of the Royal Irish Academy, contain examples of both these inquiries, although they relate chiefly to the second part, or second class of problems, namely, to the using of his function, supposed found. He has endeavoured to establish, for such using, a system of general formulæ, and has deduced many general consequences and properties of optical systems, independent of the particular shapes and positions and other peculiarities of the surfaces and media of any optical combination. A few results less general than these, and yet themselves extensive, may not improperly, perhaps, be mentioned here.
When we wish to study the properties of any object-glass, or
eye-glass, or other instrument in vacuo, symmetric in all
respects, about one axis of revolution, we may take this for the
axis of z, and we shall still have the equations (1.), the
characteristic function V being now a function of the five
quantities ![]() , xx' + yy',
, xx' + yy', ![]() , z, z',
involving also, in general, the colour, and having its form determined
by the properties of the instrument of revolution. Reciprocally,
these properties of the instrument are included in the form of the
characteristic function V, or in the form of this other connected
function,
, z, z',
involving also, in general, the colour, and having its form determined
by the properties of the instrument of revolution. Reciprocally,
these properties of the instrument are included in the form of the
characteristic function V, or in the form of this other connected
function,
![]()
which may be considered as depending on only three independent
variables besides the colour; namely, on the inclinations of the final
and initial portions of a luminous path to each other and to the axis
of the instrument. Algebraically, T is in general a function of the
colour and of the three quantities ![]() ,
,
![]() ,
, ![]() ; and it may
usually (though not in every case) be developed according to
ascending powers, positive and integer, of these three latter
quantities, which in most applications are small, of the order of the
squares of the inclinations. We may therefore in most cases confine
ourselves to an approximate expression of the form
; and it may
usually (though not in every case) be developed according to
ascending powers, positive and integer, of these three latter
quantities, which in most applications are small, of the order of the
squares of the inclinations. We may therefore in most cases confine
ourselves to an approximate expression of the form
![]()
in which ![]() is independent of the inclinations:
is independent of the inclinations: ![]() is
small of the second order, if those inclinations be small, and is of
the form
is
small of the second order, if those inclinations be small, and is of
the form
and ![]() is small of the fourth order, and is of the form
is small of the fourth order, and is of the form
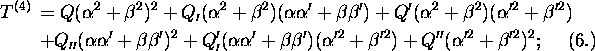
the nine coefficients P ![]()
![]() Q
Q ![]()
![]()
![]()
![]()
![]() ,
being either constant, or at least only functions of the colour. The
optical properties of the instrument, to a great degree of
approximation, depend usually on these nine coefficients and on their
chromatic variations, because the function T may in most cases be
very approximately expressed by them, and because the fundamental
equations (1.) may rigorously be thus transformed;
,
being either constant, or at least only functions of the colour. The
optical properties of the instrument, to a great degree of
approximation, depend usually on these nine coefficients and on their
chromatic variations, because the function T may in most cases be
very approximately expressed by them, and because the fundamental
equations (1.) may rigorously be thus transformed;
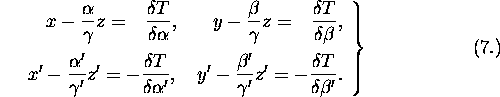
The first three coefficients P ![]()
![]() , which enter by
(5.) into the expression of the term
, which enter by
(5.) into the expression of the term ![]() , are those on
which the focal lengths, the magnifying powers, and the chromatic
aberrations depend: the spherical aberrations, whether for direct or
inclined rays, from a near or distant object, at either side of the
instrument (but not too far from the axis), depend on the six other
coefficients, Q
, are those on
which the focal lengths, the magnifying powers, and the chromatic
aberrations depend: the spherical aberrations, whether for direct or
inclined rays, from a near or distant object, at either side of the
instrument (but not too far from the axis), depend on the six other
coefficients, Q ![]() ,
, ![]()
![]()
![]()
![]() , in the expression of the
term
, in the expression of the
term ![]() . Here, then, we have already a new and remarkable
property of object-glasses, and eye-glasses, and other optical
instruments of revolution; namely, that all the circumstances of their
spherical aberrations, however varied by distance or
inclination, depend (usually) on the values of SIX RADICAL
CONSTANTS OF ABERRATION, and may be deduced from these six numbers by
uniform and general processes. And as, by employing general symbols
to denote the constant coefficients or elements of an elliptic orbit,
it is possible to deduce results extending to all such orbits, which
can afterwards be particularised for each; so, by employing general
symbols for the six constants of spherical aberration, suggested by
the foregoing theory, it is possible to deduce general results
respecting the aberrational properties of optical instruments of
revolution, and to combine these afterwards with the peculiarities of
each particular instrument by substituting the numerical values of its
own particular constants. The author proceeds to mention some of the
general consequences to which this view has conducted him, respecting
the aberrational properties of optical instruments of this kind.
. Here, then, we have already a new and remarkable
property of object-glasses, and eye-glasses, and other optical
instruments of revolution; namely, that all the circumstances of their
spherical aberrations, however varied by distance or
inclination, depend (usually) on the values of SIX RADICAL
CONSTANTS OF ABERRATION, and may be deduced from these six numbers by
uniform and general processes. And as, by employing general symbols
to denote the constant coefficients or elements of an elliptic orbit,
it is possible to deduce results extending to all such orbits, which
can afterwards be particularised for each; so, by employing general
symbols for the six constants of spherical aberration, suggested by
the foregoing theory, it is possible to deduce general results
respecting the aberrational properties of optical instruments of
revolution, and to combine these afterwards with the peculiarities of
each particular instrument by substituting the numerical values of its
own particular constants. The author proceeds to mention some of the
general consequences to which this view has conducted him, respecting
the aberrational properties of optical instruments of this kind.
When a luminous point is placed on the axis of an object-glass, or eye-glass, or other instrument of revolution, and when its rays are not refracted or reflected so as to converge exactly to, or diverge exactly from, one common focus, they become, as it is well known, all tangents to one caustic surface of revolution, and they all intersect the axis, at least when they are prolonged, if necessary behind the instrument. But if the luminous point be anywhere out of the axis, the arrangement of the final rays becomes less simple than before. They are not now all tangents to the meridian of a surface of revolution, nor do they all intersect the axis of the instrument; they become, by another known theorem, the tangents to two caustic surfaces, and to two sets of caustic curves, and compose two series of developable pencils, or ray surfaces; so that each ray of the final system may be considered as having, in general, two foci, or points of intersection with other rays, indefinitely near. The theorem here alluded to, namely, that of the general existence of two foci for each ray of a system proceeding from any surface according to any law, was first discovered by Malus. Mr. Hamilton also obtained it independently, but later, in 1823. It appears to be, as yet, but little known; but it is, he thinks, essential to a correct view of the arrangement of rays in space, for which the analogy of rays in a plane seems quite inadequate. Combining this theorem of the two foci with his view of the characteristic function, and of the six constants of spherical aberration, for the final system produced by oblique incidence on an instrument of revolution, the author has found that the two foci of a ray of this final system do not in general close up into one, except for TWO PRINCIPAL RAYS, having each its own PRINCIPAL FOCUS. The interval between the two foci of any other ray is proportional, very nearly, to the product of the sines of its inclinations to the two principal rays; and the tangent planes of the two developable pencils, passing through any variable ray, bisect (very nearly) the two pairs of supplemental dihedrate angles formed by the two planes which contain this variable ray and are parallel to the two principal rays; in such a manner that all the rays of any developable pencil of one set have (very nearly) one common sum, and all the rays of any developable pencil of the other set have (very nearly) one common difference, of inclinations to the same two principal rays, or axes of the final system. These latter axes always intersect each other, and their plane is either the diametral plane of the instrument (containing the luminous point or focus of incident rays), or a plane perpendicular to that diametral plane, according to the sign of a certain quantity, which vanishes when the two axes happen to coincide in one principal ray, round which the whole final system has then a very perfect symmetry; and, in general, the angle of the two principal rays, whether in or out of the diametral plane of the instrument, is bisected (very nearly) by a certain intermediate ray in that plane, which may be called the CENTRAL RAY of the system, because the other final rays are disposed about it with a certain symmetry of arrangement, less perfect than the symmetry about an axis of revolution, but resembling that of the normals to an ellipsoid about one of its three axes, when unequal; and accordingly the author finds that the final rays from an instrument of revolution (when the incident rays are oblique) are very nearly normals to a portion of such an ellipsoid, having the central ray for one of its three unequal axes, and having the two principal rays for its two umbilical normals, at two out of the four points where the ellipsoid has complete contact of the second order with an osculating sphere. The centres of the two osculating spheres at these two points are the two principal foci of the system; and the centres of the two extreme osculating spheres at any other point of the ellipsoid are the two foci of the corresponding ray, or the points at which that ray touches the two caustic surfaces. These latter surfaces are, in the present approximation, the surfaces of centres of curvature of the ellipsoid: they have a curve of intersection with each other, which contains the two principal foci; every point upon the curve, except these two, being the first focus of one ray and the second focus of another. A plane may be drawn perpendicular to the central ray, and passing through the two principal foci; and this plane will cut the two caustic surfaces in sections which compose a kind of little lozenge, consisting (very nearly) of two curvilinear equilateral triangles, having the principal foci for two common corners: the quadrature of these curvilinear triangles, and of the other sections of the caustic surfaces, depending on elliptic integrals. In all the foregoing remarks, it is supposed, for greater generality, that the aberrations do not vanish with the obliquity of the incident rays; but when the instrument is aplanatic for direct incident rays, it is easy to apply the same theory of the characteristic function and the six radical constants of aberration, and to determine, for this particular case, the components of spherical aberration which arise from obliquity only.
This theory of the aberrations of oblique rays, for an optical instrument of revolution, may admit of practical applications. For the mathematical symmetry of arrangement of the final rays about the central ray of their system, and the intensity of the two principal foci, may perhaps affect our sight, and have some appreciable influence on the practical performance of an instrument; but of this Mr. Hamilton speaks with diffidence, because experiments directed expressly to the question appear to be required for its decision. If the mathematical properties which he has determined by theory in the arrangement and aberrations of a system, shall be found in practice to have any sensible influence on the phænomena of oblique vision, it will become necessary to alter some of the received rules for the construction of telescopes and microscopes; or, at least, it will be possible to improve those rules by following the indications of this theory. A new track seems to be opened thus to mathematical and practical opticians.
The principle of the characteristic function, from which have been deduced the foregoing results, among others not yet published, respecting optical instruments of revolution, may be applied to every part of mathematical and perhaps of physical optics; and an analogous function and method may be introduced into other sciences, especially in dynamical astronomy. But the author confines himself to mentioning the application which he has made of the principle to the study of the laws of extraordinary refraction in the crystals called biaxal. The general laws of reflection and refraction, ordinary and extraordinary, at any point of any surface, are expressed by his function as follows, when the normal to the reflecting or refracting surface at the point of incidence is taken for the axis of z:
and in the language of the undulatory theory they may be enunciated by saying, that if the normal slowness of propagation of a luminous wave, at any point of incidence on any reflecting or refracting surface, be decomposed in any direction parallel to this surface at this point, the component of normal slowness is not altered by reflection or refraction. In the case of ordinary refraction, this comes to saying, that if on the incident ray prolonged, and on the refracted ray, we measure from the point of incidence lengths represented by the indices of the first and second media, those lengths will have one common projection on the refracting surface or on its tangent plane; which is a form for the law of Snellius. For extraordinary refraction, we must in general construct the normal slowness of a wave by a variable length not always coinciding with the ray; but the two lengths thus substituted for the two successive indices will still have one common projection on the refracting face of the crystal, if plane, or on its tangent plane, if it be curved. If now we seek the locus of the end of the line, which represents in length and direction the normal slowness of a wave, for all possible directions of this slowness, we get for ordinary media a sphere, but for extraordinary media (on Fresnel's principles) a certain double surface, which is not the same as Fresnel's curved wave-surface, propagated in all directions from a point, but is connected therewith by several remarkable relations of reciprocity, and may be called the surface of components since its coordinates are themselves the components of normal slowness of propagation. They are equal to the partial differential coefficients of the first order of the author's characteristic function V, and are connected by a partial differential equation of the form
![]()
which may be regarded as the equation of the surface. And the general equations of reflection or refraction (8.), when put under the form
![]()
express that the corresponding points on the two surfaces of components, before and after any reflection or refraction, ordinary or extraordinary, are on one common ordinate to the reflecting or refracting surface, or to its tangent plane; which gives a new and general construction for the direction of a reflected or refracted wave, and therefore for that of a reflected or refracted ray, simpler in may cases than the construction proposed by Huygens. Thus, if it were required to determine by this new construction the direction and the undulatory velocity of an extraordinary ray, refracted in Iceland spar, being given the direction of the incident ray in air, we should have to construct first the two successive surfaces of components, which would be here a sphere for the air, and a spheroid (not the Huygenian) for the crystal, the common centre of both being at the point of incidence; and then, after determining the point of the hemispheroid within the crystal, which is on the same ordinate to the refracting face as the point where the incident ray prolonged meets its own interior hemisphere, we should only have to draw a tangent plane to the spheroid at the point just determined, and to let fall a perpendicular on this plane from the point of incidence; for this perpendicular is, in length and direction, the radius vector of the Huygenian spheroid, and therefore represents the undulatory velocity and the direction of the extraordinary ray. And other more complicated cases may be treated in a similar manner, either by using a construction of this kind, or by the equivalent formulæ derived from the characteristic function.
When the author proceeded to apply this general method to Fresnel's principles respecting biaxal crystals, he arrived at the curious result that the surface of components, in such a crystal, has not at every point a determined tangent plane, but that at each of four cusps, opposite, two by two, it is touched by an infinite number of such planes, or by a tangent cone; and hence he immediately concluded, by his general method, that if a ray in air fall so upon a biaxal crystal as to make the point upon the air-sphere correspond (by the rule already explained) to one of those cusps on the surface of components of normal slowness in the crystal, his construction would give no unique refracted ray, nor even a pair or other finite number of such rays within the crystal, but an infinite number of refracted rays, namely, all the perpendiculars which can be let fall from the point of incidence on the tangent cone at the cusp. The author saw also that these rays must terminate in some curve of plane contact on Fresnel's double wave, in the whole extent of which curve the wave must be touched by one plane, and that there must be four such curves, which he afterwards found to be circles; a curious property of this wave, which Fresnel himself had not noticed. But the most remarkable part of this result was the new and delicate experimental test which it offered for Fresnel's principles, since the INTERNAL CONICAL REFRACTION which it indicated, for certain cases of incidence on a biaxal crystal, had not only not been hitherto observed, but seemed contrary to all former analogies of observation; so that if this theoretical consequence of Fresnel's principles, which he had not himself perceived, should be verified by subsequent experiment, the principles would receive a new and striking confirmation; and if, on the contrary, after all due care employed in experiments directed expressly to the question, the small but finite conical dispersion in biaxal crystals, which the author had thus theoretically concluded, should not be found in fact to take place, the principles themselves would require to be abandoned or modified. Professor Lloyd was applied to by the author to undertake this experimental inquiry. After some unsuccessful trials with crystals of insufficient size and purity, he obtained a fine piece of arragonite from Mr. Dollond, and at length completely succeeded in exhibiting the phænomenon which Mr. Hamilton had expected. The rays of the internal cone emerged, as they ought, in a cylinder from the second face of the crystal; and the size of this nearly circular cylinder, though small, was decidedly perceptible, so that with solar light it threw on silver paper a little luminous ring, which seemed to remain the same at different distances of the paper from the arragonite. Professor Lloyd describes the appearance as very beautiful when he employed a lamp, and received the emergent rays on a lens: he seemed to see the two points of light, which the double refraction usually produced, spread out on a sudden, when the critical incidence was obtained, into a ring of gold viewed on a dark ground. His account is contained (with Professor Hamilton's theoretical investigation) in the First Part of the seventeenth volume of the Transactions of the Royal Irish Academy; a shorter statement was also published in the numbers of the London and Edinburgh Philosophical Magazine for the months of February and March 1833.
From the connexion of the surface of components with the wave surface propagated from a point, the author saw that the existence of four conoidal cusps on the one surface in Fresnel's theory involved the existence of four such cusps upon the other, namely at the points of intersection of Fresnel's circle and ellipse in the plane of the extreme axes of elasticity: and that he was led to expect an EXTERNAL CONICAL REFRACTION, corresponding to the internal incidence of a cusp-ray when emerging into air from a crystal with two axes. On this point also he requested Professor Lloyd to undertake a series of experiments; and on this point also (indeed, somewhat sooner than on the other,) he obtained a complete verification. His experimental determinations of the size and position of this emergent cone, as of the former emergent cylinder, and of the law of polarization in each, for the same large piece of arragonite, agreed with the theoretical results deduced from the principles of Fresnel by the method of the Characteristic Function.
Although this method appears likely to be adopted by analysts at some future time in the researches of theoretical optics, the author does not pretend that its results cannot be obtained in other ways; and with respect to the two kinds of conical refraction, in particular, Mr. MacCullagh (F.T.C.D.) has published in the London and Edinburgh Philosophical Magazine for the months of August and September in the present year, an elegant geometrical investigation together with some account of the progress of his thoughts upon the subject. The surface which Professor Hamilton has called the surface of components, (of normal slowness of propagation,) and to which he was conducted some years ago, as constructing a fundamental equation between the partial differential coefficients of his Characteristic Function, occurred to Mr. MacCullagh also, as he has informed the author, independently from considerations of a geometrical kind. The same important surface presented itself to M. Cauchy, likewise, in his dynamical researches respecting a system of attracting or repelling points.
Links:
D.R. Wilkins