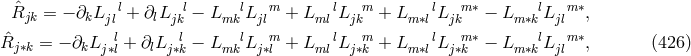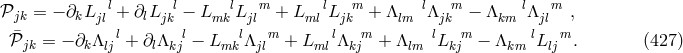10 Einstein–Schrödinger Theory in Paris
Research on unified field theory in Paris centered around the mathematician A. Lichnerowicz, a student of Georges Darmois, and the theoretical physicist Marie-Antoinette Tonnelat. It followed two main lines: the affine or metric-affine approaches of Einstein and Schrödinger, and the 5-dimensional unification originating with G. Nordström and Th. Kaluza. The latter theme was first studied in Paris by Y. Thiry, a former student of A. Lichnerowicz (“Jordan–Thiry-theory”), and by students of M.-A. Tonnelat; the first topic, “Einstein–Schrödinger theory”, mainly by Tonnelat and her coworkers but no strict divide did exist. Between 1950 and the mid 1960s at least two dozen doctoral theses on topics in unitary field theory were advised by Lichnerowicz and/or by Tonnelat. Whereas the work of Tonnelat’s students could be classified as applied mathematics, Lichnerowicz’s interest, outside of pure mathematics, was directed to mathematical physics with its rigid proofs. This joined attack on unsolved questions and problematic features of classical unified field theory has made clear that (1) the theories under scrutiny were mathematically consistent, but (2) they could not be transformed into an acceptable part of physics.
10.1 Marie-Antoinette Tonnelat and Einstein’s Unified Field Theory
We first make contact with Marie-Antoinette Tonnelat and her research group in the Institut Henri Poincaré. She had
studied with Louis de Broglie. During the German occupation of Paris she continued to work
with de Broglie and on her own in the field of (relativistic) “spin-particles”, also under the
influence of a gravitational field. She applied de Broglie’s “méthode de fusion” to massive
spin 1 particles (called photons) in order to arrive at particles with maximal spin 2: spin 2
corresponded to the graviton. The theory contained the graviton, three photons and two scalar
particles (spin 0) all with non-vanishing mass. Each relevant field component satisfied the Klein
Gordon equation. From there, she arrived at Maxwell’s equations and the linearized version of
the equation for Einstein spaces 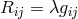 . She carefully looked at the theory for a particle
with spin 2 as a “unitary theory” and preferred to call it “a unitary formalism” ([616*], p. 163,
164):
. She carefully looked at the theory for a particle
with spin 2 as a “unitary theory” and preferred to call it “a unitary formalism” ([616*], p. 163,
164):
“[…] the theory of maximal spin 2 allows to show how a unitary theory presents itself,
approximately, but in the framework of wave mechanics.”169
Many of her papers were published in the proceedings of the prestigious Academy of Sciences in Paris170 [613, 612, 614, 610, 611, 615*, 616*, 617*]. The Academy’s sessions had been interrupted for a mere three weeks due to the German occupation. According to its president:
“Despite the ordeal which oppresses the country, the Comptes Rendus attest that scientific
research has not bent, and that the Academy of Sciences remains a focus of ardent and
fruitful work. […] Let us work.”171
Right after the war in 1946, like other young French scientists, Mme. Tonnelat apparently spent some time in Dublin with the group of E. Schrödinger. On the background of her previous work on a “unitary formalism” emerging from spin-2 particles, her interest in the unified field theories of Einstein and Schrödinger might have been brought forward during this stay with Schrödinger. Her scientific teacher, L. de Broglie, supported her research in UFT, although he himself stayed away from it. After briefly listing “innumerable attempts […] to complete the general theory of relativity […] and transform it into a ‘unified theory’ ”, he went on to say:
“Einstein’s efforts in this direction, ever characterized by the salient originality of his thought, will not be examined here. Despite their indisputable interest, they have not, to the best of our knowledge, attained any decisive success […]. Moreover, the nature of the electromagnetic field is so intimately bound to the existence of quantum phenomena that any non-quantum unified theory is necessarily incomplete. These are problems of redoubtable complexity whose solution is still ‘in the lap of the gods’ ” ([113], p. 121).
At the 8th Solvay Congress in 1948 in Brussels, Mme. Tonnelat presented a paper by L. de Broglie on the photon as composed of two neutrinos. Schrödinger asked a question afterwards about a tiny mass of the photon ([446*], p. 444). During her work on unified field theory Tonnelat continued to study spin-particles, e.g., to regard a spin-1-particle as composed of two spin-1/2-particles [625].
10.2 Tonnelat’s research on UFT in 1946 – 1952
As we will see, M.-A. Tonnelat made several attempts until she reached the final version of her unified
field theory. In the warm-up, i.e., in her first paper on the subject, Tonnelat referred only to
Schrödinger’s theory [545, 549] and to Eyraud’s thesis of 1926 (cf. Section 5 of Part I). By her
theory, she intended to describe the gravitational, electromagnetic and mesonic fields [618]. The
paper was reviewed by the American theoretical physicist A. H. Taub in Mathematical Reviews
[ 0017205]:
0017205]:
“The author states without proof some formal consequences of a variational principle in which the action function is an unspecified function of a symmetric second order tensor and three (of which two are independent) anti-symmetric second order tensors. These four tensors are defined in terms of a general affine connection in a four dimensional space, and its derivatives. The connection is not assumed to be symmetric. The paper does not explain how the invariant element of volume entering into the action principle is defined.”
By her, the torsion tensor 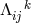 is defined through
is defined through
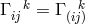 and
and ![k k Λij = Λ[ij].](article1569x.gif) Vector torsion is denoted by her as
Vector torsion is denoted by her as 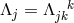 and corresponds to
our
and corresponds to
our 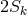 . She introduced four tensors of rank two
. She introduced four tensors of rank two 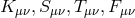 corresponding in our notation (in
the same order) to:
with the torsion vector
corresponding in our notation (in
the same order) to:
with the torsion vector 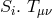 corresponds to homothetic curvature
corresponds to homothetic curvature 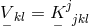 defined by (66*) in
Section 2.3.1. In the spirit of Schrödinger, a metric density is introduced by:
The Lagrangian is defined as a functional of these four tensors. By help of a “geometrically” defined matter
tensor the resulting field equations are rewritten in the form of Einstein’s equations.
defined by (66*) in
Section 2.3.1. In the spirit of Schrödinger, a metric density is introduced by:
The Lagrangian is defined as a functional of these four tensors. By help of a “geometrically” defined matter
tensor the resulting field equations are rewritten in the form of Einstein’s equations.
In three following papers, Tonnelat had become acquainted with some of the past literature on the
subject, and included references to Einstein [619, 620, 621]. Her intention was to generalize this past
work for an arbitrary affine connection in a more systematical way such as to “augment the
interpretative possibilities of the theory.” The same tensors as before (one symmetric, three
antisymmetric) were introduced with a bewildering change of her own notation: 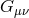 instead of
instead of
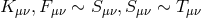 , and
, and 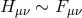 . Again, the Lagrangian is a functional of these four tensors
and, possibly, the torsion vector. After dual (conjugate) field tensor densities were defined through:
. Again, the Lagrangian is a functional of these four tensors
and, possibly, the torsion vector. After dual (conjugate) field tensor densities were defined through:
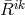 introduced by its symmetric and antisymmetric parts
introduced by its symmetric and antisymmetric parts 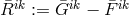 , the
field equations could be written in the form:
It is to be noted that this equation is purely formal: no definite expression for the Lagrangian had been
chosen.
, the
field equations could be written in the form:
It is to be noted that this equation is purely formal: no definite expression for the Lagrangian had been
chosen.
In the 2nd of the three notes, Tonnelat introduced a symmetric metric and split (340*) into its symmetric and antisymmetric parts (S) and (A). According to her, the exact general solution to (A) was very difficult to produce; this is seen from the complicated expression in terms of quantities like the metric, its first derivative and torsion, known in principle. In the third note, the formalism is exemplified in second-order approximation and with additional restrictions, e.g., in de Sitter space. Proca’s equation for the mesonic field emerges. In her next paper, (340*) is rewritten in the form of a metric compatibility condition:
where the covariant derivative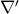 is defined with help of a new connection
is defined with help of a new connection 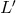 .
.
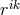 is related to
is related to 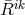 by
by 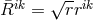 with
with 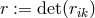 and
and 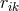 the inverse of
the inverse of
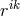 .172
The decomposition
.172
The decomposition
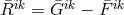 is also used. By a combination of symmetric and antisymmetric parts
is also used. By a combination of symmetric and antisymmetric parts
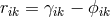 two further tensors and their inverses are introduced, i.e.,
two further tensors and their inverses are introduced, i.e., 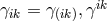 and
and
![ϕik = ϕ[ik],ϕik](article1598x.gif) . Now
. Now
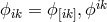 , and
, and 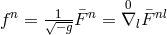 with
with 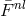 having been defined in (339*). Apart
from ingenious manipulations of a very general formalism, no physical progress with regard to
Schrödinger’s and Einstein’s theories had been reached in this paper [622*]. As Tonnelat herself
confessed: “The physical interpretation of the thus formed tensors is far from being immediately
clear.”173
having been defined in (339*). Apart
from ingenious manipulations of a very general formalism, no physical progress with regard to
Schrödinger’s and Einstein’s theories had been reached in this paper [622*]. As Tonnelat herself
confessed: “The physical interpretation of the thus formed tensors is far from being immediately
clear.”173
Two summaries of her attempts with regard to affine field theory were presented by Tonnelat in 1951
and 1952 [627*, 628*]. It would be natural to discuss them together but M.-A. Tonnelat again complicated
matters by an altered notation from one paper to the next. In 1951, for the first time, she
introduced the transposed connection 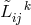 and thus worked with both
and thus worked with both 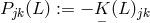 and
and 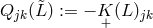 . Further basic tensors chosen were
. Further basic tensors chosen were 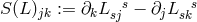 and
and
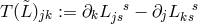 , and a fifth quantity
, and a fifth quantity 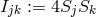 with
with 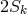 corresponding
to her
corresponding
to her 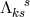 . Having read the 2nd edition of Einstein’s The Meaning of Relativity – as she
claimed,174
she accepted Einstein’s suggestion that only Hermitian quantities should be used as fundamental quantities
in a Lagrangian. The following objects were introduced by her:
. Having read the 2nd edition of Einstein’s The Meaning of Relativity – as she
claimed,174
she accepted Einstein’s suggestion that only Hermitian quantities should be used as fundamental quantities
in a Lagrangian. The following objects were introduced by her:
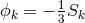 , a new connection
, a new connection 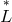 with vanishing torsion vector is obtained.
Furthermore,
with vanishing torsion vector is obtained.
Furthermore, 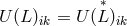 . In place of the field densities (339*), now the three quantities are used:
which are then manipulated similarly as in the previous
paper.176
Eventually, Eq. (341*) is obtained again, where the connection
. In place of the field densities (339*), now the three quantities are used:
which are then manipulated similarly as in the previous
paper.176
Eventually, Eq. (341*) is obtained again, where the connection 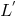 now is derived by beginning with
now is derived by beginning with 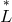 .
The new Eq. (341*) remains unchanged if the connection
.
The new Eq. (341*) remains unchanged if the connection 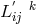 and
and 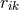 are replaced by the transposed
objects. Up to here, a general formalism has been developed. In order to proceed, M.-A. Tonnelat then
picked the same Lagrangian
are replaced by the transposed
objects. Up to here, a general formalism has been developed. In order to proceed, M.-A. Tonnelat then
picked the same Lagrangian 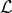 as Schrödinger had in Eq. (229*), i.e.,
as Schrödinger had in Eq. (229*), i.e., 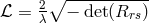 , yet based on
her vector-torsion-free connection
, yet based on
her vector-torsion-free connection 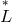 . The field equations derived by her decompose into the fundamental
ones (variation with regard to
. The field equations derived by her decompose into the fundamental
ones (variation with regard to 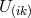 ) and such of a “Maxwellian” type (variation with regard to
) and such of a “Maxwellian” type (variation with regard to 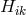 ).
With the decomposition
).
With the decomposition 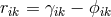 of the previous paper and the additional
of the previous paper and the additional 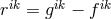 together with the inverses of these four tensors, eight basic fields float around in the theory waiting for
physical interpretation. Although still in a purely affine theory, the particular interpretation relating
together with the inverses of these four tensors, eight basic fields float around in the theory waiting for
physical interpretation. Although still in a purely affine theory, the particular interpretation relating 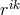 or
or 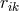 with a metric could make the transition to mixed geometry [cf. Section 2.1 and Eqs. (3*),
(4*)]).177
The field equations look very complicated such that an approximative handling seemed appropriate. For
weak fields
with a metric could make the transition to mixed geometry [cf. Section 2.1 and Eqs. (3*),
(4*)]).177
The field equations look very complicated such that an approximative handling seemed appropriate. For
weak fields 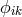 , i.e., up to 2nd order, a Proca-type equation was obtained. For the approximated Ricci
tensor, field equations of the form of Einstein’s equations with cosmological constant and including the
“metric”
, i.e., up to 2nd order, a Proca-type equation was obtained. For the approximated Ricci
tensor, field equations of the form of Einstein’s equations with cosmological constant and including the
“metric”  were reached. The matter tensor is a complicated functional of the connections
were reached. The matter tensor is a complicated functional of the connections 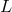 and
and 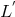 . Thus, formally, “matter” has been geometrized. Tonnelat did not give physical interpretations to
the tensors appearing except for identifying
. Thus, formally, “matter” has been geometrized. Tonnelat did not give physical interpretations to
the tensors appearing except for identifying 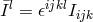 ,
, 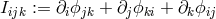 , or its dual
, or its dual
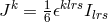 with the electric current density.
with the electric current density.
In a separate note, M.-A. Tonnelat discussed a possible relation 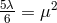 between the cosmological
constant
between the cosmological
constant 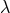 appearing in the Proca equation obtained from her unified field theory in an approximation up
to 2nd order in
appearing in the Proca equation obtained from her unified field theory in an approximation up
to 2nd order in 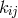 :
:
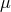 in a space of constant curvature
derived by her [615]:
While she abstained from over-interpreting this relation in the sense of bringing both types of
theories closer to each other, she still had some hope concerning the understanding of elementary
particles:
in a space of constant curvature
derived by her [615]:
While she abstained from over-interpreting this relation in the sense of bringing both types of
theories closer to each other, she still had some hope concerning the understanding of elementary
particles:
“[…] the possibility remains of finding, thanks to the exact solution to the equation
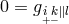 , a solution valid even in the case of strong fields, an explanation of the nature
of the elementary particles. However, as Schrödinger very strongly emphasized, the
realization of this hope remains quite problematical despite all efforts.” ([626], p. 832)
178
, a solution valid even in the case of strong fields, an explanation of the nature
of the elementary particles. However, as Schrödinger very strongly emphasized, the
realization of this hope remains quite problematical despite all efforts.” ([626], p. 832)
178
In her subsequent paper [628*], Tonnelat pledged to adopt “Einstein’s
notations”.179
Two connections were used, both free of vector torsion: ![(1) k k 2 k Δ ij := L ij + 3δ[iLj ]](article1658x.gif) and
and
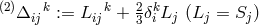 .
. 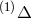 is the same as Schrödinger’s “star”-connection; cf. Eq. (232*) in
Section 8.1180
She then discussed at length which Ricci-tensor to take as basic variable, and listed
four possible expressions:
is the same as Schrödinger’s “star”-connection; cf. Eq. (232*) in
Section 8.1180
She then discussed at length which Ricci-tensor to take as basic variable, and listed
four possible expressions: 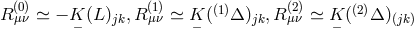 , and
the Hermitian
, and
the Hermitian 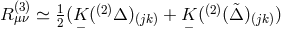 . The formalism then is carried out
with all
. The formalism then is carried out
with all 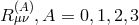 . For the first time,
. For the first time, 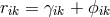 is identified as the metric
tensor.181
As before, it ensued from
is identified as the metric
tensor.181
As before, it ensued from 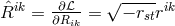 and its reciprocal. The field equations following from
variation with regard to the
and its reciprocal. The field equations following from
variation with regard to the 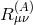 looked like:
looked like:
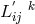 in the covariant derivative is formed with the help of
in the covariant derivative is formed with the help of 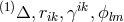 ,
and
,
and 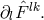 The same Lagrangian as before is used such that the field equations simply are:
For the further evaluation, for each of the four tensors
The same Lagrangian as before is used such that the field equations simply are:
For the further evaluation, for each of the four tensors 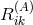 the corresponding connection as a functional
of the fields must be inserted into (354*). This leads to very complicated manipulations such that, again,
Tonnelat decided to take the antisymmetric part
the corresponding connection as a functional
of the fields must be inserted into (354*). This leads to very complicated manipulations such that, again,
Tonnelat decided to take the antisymmetric part 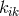 of
of 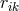 to be small of the order
to be small of the order  , expand in
, expand in  and neglect all terms of the order
and neglect all terms of the order 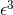 . The relation between the cosmological constant
. The relation between the cosmological constant 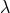 expressed by
the curvature radius of de Sitter space
expressed by
the curvature radius of de Sitter space 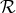 , i.e.,
, i.e., 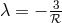 now is alternatively,
now is alternatively, 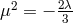 , or
, or
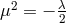 .
.
A comparison of M.-A. Tonnelat’s research with respect to Einstein’s and Schrödinger’s shows that, though first generalizing the class of possible Lagrangians enormously by including four tensor fields, in the end she went back to only one: she used Schrödinger’s Lagrangian corresponding to Einstein’s Lagrangian for general relativity. She avoided the additional equation within the field equations which demands that the torsion vector vanish by directly starting with a connection with zero torsion vector. Although this approach was new,182 most characteristic and important for her research seems to be that she directed her attention to “metric compatibility” in the sense of (200*) of Section 7.2 and succeeded to “solve” it for the connection; cf. Section 10.2.3. She also showed that out of a purely affine theory, by proper definitions and interpretations, a theory within mixed geometry could be made. It was such a theory that she finally adopted.
10.2.1 Summaries by Tonnelat of her work
M.-A. Tonnelat summed up her research within Einstein–Schrödiner theory of almost a decade, published
in many short notes in Comptes Rendus and in papers in other journals, in a monograph in 1955
[632*]; it eventually became translated into English [642*]. Unassumingly, she assessed the book
as “[…] a collection of works with the sole aim of facilitating research on the subject” ([632*],
p. IX.)183 In the Mathematical Reviews [
In the Mathematical Reviews [ MR0076499], A. H. Taub not only gave a detailed description of its contents
but also put the book into a larger perspective:
MR0076499], A. H. Taub not only gave a detailed description of its contents
but also put the book into a larger perspective:
“In this book the author summarizes and discusses a great body of material on the Einstein and Schrödinger unified field theories. […] The previous work of the author is collected and presented in a logical coherent fashion. The results obtained by other workers are also presented and compared. Thus, in this single volume containing an introduction and seven chapters one can obtain a well written complete and succinct account of the recent work in the field.”
Tonnelat’s associate J. Winogradzki, in her report on the book, gave a condensed list of the
contents and found “that the major part of the work is devoted to the mathematical study
of the field equations. The two last chapters deal with some physical content of the theory”
[705]. Tonnelat clearly drew the line with regard to work by Lichnerowicz, e.g., the initial value
problem. For her, the balance between the remaining problems of UFT and the results obtained
was positive: “[…] Einstein’s theory binds together the realization of a satisfying synthesis,
originating from a very general principle, and the possibility of new provisions.” ([632*], p. 11)
184 For her, UFT was a fruitful and important theory.
For her, UFT was a fruitful and important theory.
After another decade, in 1965, she published a second monograph on unified field theories reflecting now the development of research in all more prominent approaches to unified field theory. Her work and the results of her group concerning the Einstein–Schrödinger theory took up only one chapter [641*]. A few of the doctoral theses she had advised were referred to. In its third part, the book aimed at presenting some connection between classical and quantum field theory. As a first approximation to an unknown nonlinear theory, Tonnelat’s alternative theory of gravitation (linear gravity) investigated by her in the 1960s is included (cf. Section 16.1). In comparison with her first book, she had become even more modest:
“Whatever the future of the unitary theories might be, this book will have reached its
objective, if it has somehow shown that the ties between electromagnetism and gravitation
form a history of rebouncings the outcome of which is far from being written.” ([641*],
p. IX)185
In the following, some of the main aspects of her approach to UFT will be described.
10.2.2 Field equations
As she had moved from pure affine to mixed geometry during her research, M.-A. Tonnelat then started
from the Lagrangian density 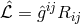 where the reciprocal metric density
where the reciprocal metric density 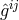 is defined in (13*), and
is defined in (13*), and
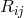 is one out of the list of possible Ricci-tensors.
is one out of the list of possible Ricci-tensors. 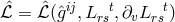 . Variation with
respect to
. Variation with
respect to 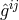 and
and 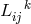 led her to the field equations. With
led her to the field equations. With 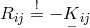 she arrived at:
she arrived at:
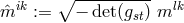 with
with 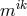 being the skew-symmetric part of the inverse metric, and
being the skew-symmetric part of the inverse metric, and
![Si := L j [ij]](article1697x.gif) .186.
After going over to the connection previously named
.186.
After going over to the connection previously named 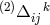 , i.e., Schrödinger’s “star”-connection,
Einstein’s weak field equations followed from the variational principle in the form:
where
, i.e., Schrödinger’s “star”-connection,
Einstein’s weak field equations followed from the variational principle in the form:
where 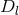 stands for the covariant derivative with respect to the new connection;
stands for the covariant derivative with respect to the new connection; 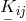 is the
Ricci tensor
is the
Ricci tensor 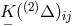 formed with
formed with 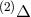 and named
and named 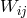 by Tonnelat (cf. [632*], Eq. II,
p. 31). If
by Tonnelat (cf. [632*], Eq. II,
p. 31). If 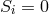 is added to Eqs. (355*) and (356*) Einstein’s strong field equations obtain;
they no longer follow from the variational principle. M. Lenoir used the fiber bundle of affine
reference frames and the transformation groups implied by it to arrive at Tonnelat’s field equations
[358].
is added to Eqs. (355*) and (356*) Einstein’s strong field equations obtain;
they no longer follow from the variational principle. M. Lenoir used the fiber bundle of affine
reference frames and the transformation groups implied by it to arrive at Tonnelat’s field equations
[358].
10.2.3 Removal of affine connection
A first objective was to use the equation 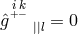 or, equivalently, (30*) to express the affine connection
or, equivalently, (30*) to express the affine connection
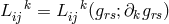 as a functional of the asymmetric metric
as a functional of the asymmetric metric 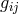 and its first derivatives in the same
way as the Christoffel symbol had been expressed by the metric and its first derivatives. Now, the system
comprises 64 linear equations for 64 variables
and its first derivatives in the same
way as the Christoffel symbol had been expressed by the metric and its first derivatives. Now, the system
comprises 64 linear equations for 64 variables 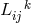 . As an already solved algebraic problem this might not
create much interest for “pure” mathematicians: an inverse matrix must be found, if only a large one
with functions as its elements. V. Hlavatý called for an “elementary algebraic device” to be
invented. As a problem in applied mathematics, even in the computer age, it takes quite an effort
to do this by computer algebra. The wish to obtain the solution in tensorial form aggravates
matters. According to Hlavatý: “Finding such a device is by no means an easy task” ([269*],
p. 50).
. As an already solved algebraic problem this might not
create much interest for “pure” mathematicians: an inverse matrix must be found, if only a large one
with functions as its elements. V. Hlavatý called for an “elementary algebraic device” to be
invented. As a problem in applied mathematics, even in the computer age, it takes quite an effort
to do this by computer algebra. The wish to obtain the solution in tensorial form aggravates
matters. According to Hlavatý: “Finding such a device is by no means an easy task” ([269*],
p. 50).
In Riemann–Cartan theory, i.e., in a theory with symmetric metric and arbitrary linear connection, we obtain:
If![L [ilk] ⁄= 0](article1712x.gif) , the usual method of solving (359*) for the Christoffel symbol as a functional of the metric and its first derivatives
still works,187
but no longer for (30*).
, the usual method of solving (359*) for the Christoffel symbol as a functional of the metric and its first derivatives
still works,187
but no longer for (30*).
After E. Straus had not been able to present a manageable solution (cf. Section 7.3), M. A. Tonnelat
invested a lot of work into the same methodical approach. In a series of steps involving many intermediate
expressions which had to be replaced in the end, she obtained a solution. In her first attempt during the
early 1950s [622, 623], summed up in her monographs [632*, 642], the solution is achieved by first splitting
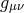 into its irreducible parts. If
into its irreducible parts. If 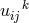 is defined similarly as in (39*) but with a different
is defined similarly as in (39*) but with a different 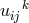 by
by
 is the torsion tensor of the connection
is the torsion tensor of the connection 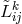 , and
, and 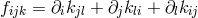 . We have met (361*),
(362*) in principle already in Section 2.1.2. A. H. Taub had reviewed one of her papers on the subject from
1950 [
. We have met (361*),
(362*) in principle already in Section 2.1.2. A. H. Taub had reviewed one of her papers on the subject from
1950 [ MR0037634]: “These systems are then solved explicitly. Straus [592] has also solved this problem by
another method after remarking that the method used in this paper is feasible.” The main conclusion is
that the symmetric part of the affine connection may be expressed by its antisymmetric part from (361*),
while (362*) then determines the antisymmetric part, in terms of “the fields”
MR0037634]: “These systems are then solved explicitly. Straus [592] has also solved this problem by
another method after remarking that the method used in this paper is feasible.” The main conclusion is
that the symmetric part of the affine connection may be expressed by its antisymmetric part from (361*),
while (362*) then determines the antisymmetric part, in terms of “the fields” 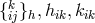 . In the next
step thus
. In the next
step thus 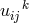 is removed from (362*). By a lengthy calculation, torsion is expressed by “the fields”. Thus,
the connection
is fully known.189
The procedure works if
where
is removed from (362*). By a lengthy calculation, torsion is expressed by “the fields”. Thus,
the connection
is fully known.189
The procedure works if
where ![∘ --- a =: 2 − g+ 6k,b =: 2 -k-[3 − g + k] h h −h h h](article1725x.gif) and
and 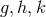 are the determinants of
are the determinants of 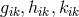 ,
respectively.
,
respectively.  and
and 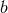 turn up during the elimination process in which
turn up during the elimination process in which 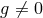 and
and 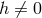 is
always assumed.
is
always assumed. 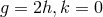 obviously leads to
obviously leads to 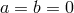 and thus leaves the solution
indeterminate; this is a result also obtained in an independent calculation by H. Takeno and coworkers
[602*]. They acknowledged Tonnelat’s solution in a note added in proof but found her condition
and thus leaves the solution
indeterminate; this is a result also obtained in an independent calculation by H. Takeno and coworkers
[602*]. They acknowledged Tonnelat’s solution in a note added in proof but found her condition
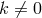 “too stringent”. M.-A. Tonnelat dealt with the case
“too stringent”. M.-A. Tonnelat dealt with the case 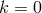 in another paper and
confirmed her general result, i.e., the condition
in another paper and
confirmed her general result, i.e., the condition 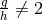 for a solution to exist [630*]. Further
careful investigations of possible subcases were made later by Hlavatý [269*] and Mishra [434*];
cf. Section 13.3.
for a solution to exist [630*]. Further
careful investigations of possible subcases were made later by Hlavatý [269*] and Mishra [434*];
cf. Section 13.3.
A reproduction of Tonnelat’s calculations would not bring further insight, the more so as
lots of auxiliary symbols were introduced by her including indices with one and two strokes.
M.-A. Tonnelat has presented the method in detail not only in her books but also in an article [633],
and in a talk given at the outstanding Relativity Jubilee Conference in 1955 in Bern ([631*],
p. 192 – 197). She was keen on securing priority, i.e., for having found the solution already in
1949 – 1950. This seemed imperative to her because in the meantime V. Hlavatý [257, 259], and
N. S. Bose [52, 50*] had also published solutions of 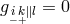 by other methods (for Hlavatý
cf. Section 12.2). In fact, Hlavatý had reviewed Tonnelat’s paper in Mathematical Reviews
[
by other methods (for Hlavatý
cf. Section 12.2). In fact, Hlavatý had reviewed Tonnelat’s paper in Mathematical Reviews
[ MR0066128], in which she had shown that
MR0066128], in which she had shown that 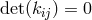 did not affect her solution [630],
and he added that “for the solution in the exceptional cases
did not affect her solution [630],
and he added that “for the solution in the exceptional cases 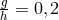 ” one should consult a
forthcoming paper of his [265]. While the limit
” one should consult a
forthcoming paper of his [265]. While the limit 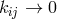 leads back to the well known results in
general relativity, the other limit
leads back to the well known results in
general relativity, the other limit 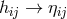 seemingly has not been discussed intensively by
Tonnelat.
seemingly has not been discussed intensively by
Tonnelat.
Indeed, the whole procedure is drastically shortened and becomes very transparent if 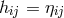 is
assumed. In this context, apparently, no one did look at this particular case. N. N. Ghosh
began with another simplified metric built like the general spherically symmetric metric, i.e.,
with only
is
assumed. In this context, apparently, no one did look at this particular case. N. N. Ghosh
began with another simplified metric built like the general spherically symmetric metric, i.e.,
with only 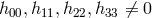 and
and 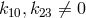 , but with all components being functions of
the four coordinates
, but with all components being functions of
the four coordinates 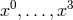 However, he managed to solve (30*) for the connection only
by adding 4 conditions for the first derivatives of
However, he managed to solve (30*) for the connection only
by adding 4 conditions for the first derivatives of 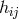 and
and 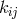 in an ad hoc manner [222*].
S. N. Bose rewrote (30*)
into an inhomogeneous linear equation for tensorial objects
in an ad hoc manner [222*].
S. N. Bose rewrote (30*)
into an inhomogeneous linear equation for tensorial objects ![Ti[jk],Ui[jk]](article1748x.gif) , i.e.,
, i.e., ![lh(Ti[jk]) = Ui[jk]](article1749x.gif) where
where
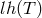 is homogeneous and linear in
is homogeneous and linear in 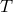 [50]. Considered as matrix equation, its solution is
[50]. Considered as matrix equation, its solution is
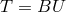 . The matrix
. The matrix 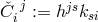 , its eigenvalues and eigenvectors play an important role.
Although the method is more transparent than Tonnelat’s, the solution is just as implicitly given as
hers.
Interestingly, at first Einstein seems to have had some doubts about her method of
solution, because torsion expressed by the fields
, its eigenvalues and eigenvectors play an important role.
Although the method is more transparent than Tonnelat’s, the solution is just as implicitly given as
hers.
Interestingly, at first Einstein seems to have had some doubts about her method of
solution, because torsion expressed by the fields 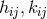 , and their first derivatives
depended on the choice of the object used as the (symmetric) metric and raised a question
of compatibility: “Mr. A. Einstein has directed my attention to this difficulty.” ([624],
p. 2407).190
, and their first derivatives
depended on the choice of the object used as the (symmetric) metric and raised a question
of compatibility: “Mr. A. Einstein has directed my attention to this difficulty.” ([624],
p. 2407).190 In the paper, M.-A. Tonnelat could disperse Einstein’s reservations. In a letter to A. Einstein of 21 June
1951, L. de Broglie wrote:
In the paper, M.-A. Tonnelat could disperse Einstein’s reservations. In a letter to A. Einstein of 21 June
1951, L. de Broglie wrote:
“I am glad to learn that one of my former pupils, Mme. Tonnelat, who really is a remarkable person, has had contact with you with regard to her papers on the unitary theories, and that you have shown an interest in her results”.191
P. G. Bergmann’s report on the Jubilee Conference was noncommittal: “A. Tonnelat of the Sorbonne reported on some mathematical results she had obtained on this theory independently of Einstein and Kaufman.” And a little later: “The papers by Kaufman and Tonnelat are too technical to be reported here.”([22*], p. 493.)
In a later approach by M.-A. Tonnelat [636], the affine connection is expressed by the metric as above
but without a decomposition of 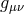 – in a similar but very much more complicated way as in the case of
the Levi-Civita connection (the Christoffel symbol). This second method does not work if
– in a similar but very much more complicated way as in the case of
the Levi-Civita connection (the Christoffel symbol). This second method does not work if 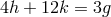 .
An improvement of it was given by Dautcourt [110] who also showed that
.
An improvement of it was given by Dautcourt [110] who also showed that 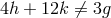 does not
guarantee a solution. V. Hlavatý used still another method to express the affine connection as a functional
of the metric; cf. Section 12.2.
does not
guarantee a solution. V. Hlavatý used still another method to express the affine connection as a functional
of the metric; cf. Section 12.2.
St. Mavridès applied Tonnelat’s method in the case of 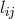 and
and 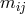 ,
i.e., the inverses of
,
i.e., the inverses of 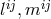 in
in 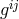 being used as metric and electromagnetic
field.192
As an existence-condition (364*) appeared as well [406]. A plenitude of further work concerning this problem
of how to express the affine connection by the asymmetric metric, its derivatives and torsion was done, with
the uniqueness proof by Hlavatý & Saenz among them [270]. It amounted to a mathematical discussion of
all logically possible cases and subcases without furthering UFT as a physical theory; cf. Sections 12.2 and
13.3.
being used as metric and electromagnetic
field.192
As an existence-condition (364*) appeared as well [406]. A plenitude of further work concerning this problem
of how to express the affine connection by the asymmetric metric, its derivatives and torsion was done, with
the uniqueness proof by Hlavatý & Saenz among them [270]. It amounted to a mathematical discussion of
all logically possible cases and subcases without furthering UFT as a physical theory; cf. Sections 12.2 and
13.3.
As a functional of the metric, its first and second derivatives, the Ricci tensor becomes a rather
complicated expression. To then find exact solutions of the remaining field equation in (340*) is a difficult
task. In a paper dealing with approximations of the field equations, M.-A. Tonnelat tried to show the
superiority of her method by applying a scheme of approximations to her (weak) field equations [634*].
However, the resulting equations of 4th order for weak electromagnetic fields 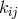 and of 1st order for weak
gravitational fields
and of 1st order for weak
gravitational fields 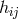 are still as complicated as to not allow a physical interpretation. In fact, the
solution of the problem to remove the connection from the field equations neither helped the search for
exact solutions nor contributed to a convincing physical interpretation of the theory. Nonetheless, it was of
crucial importance for the proofs given by A. Lichnerowicz that the initial value problem could be well
posed in UFT.
are still as complicated as to not allow a physical interpretation. In fact, the
solution of the problem to remove the connection from the field equations neither helped the search for
exact solutions nor contributed to a convincing physical interpretation of the theory. Nonetheless, it was of
crucial importance for the proofs given by A. Lichnerowicz that the initial value problem could be well
posed in UFT.
In a later development, Eq. (200*) had been made inhomogeneous:
According to Tonnelat,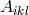 in (365*) is a linear function of the first derivatives of the metric and an
additional vector field with 2 free parameters; cf. Section 10.3.3, particularly Eq. (383*). The simple
expression J. Lévy [361*] used, by starting from
in (365*) is a linear function of the first derivatives of the metric and an
additional vector field with 2 free parameters; cf. Section 10.3.3, particularly Eq. (383*). The simple
expression J. Lévy [361*] used, by starting from 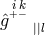 , was:
leads back to the first equation of (355*). As was shown in Section 9.6, the most promising approach seemed
to investigate special cases (spherical or axial symmetry), or approximate solutions. This also was done by
Tonnelat at the end of one of her papers of 1955 [631], and tried again, later, in a dissertation advised by
her [59*]. There, the components of the connection were calculated and compared with the results
of Bonnor [32]. In fact, for high symmetry, the whole work of solving (30*) is unneeded: the
field equations were solved at the same time for both the the metric
, was:
leads back to the first equation of (355*). As was shown in Section 9.6, the most promising approach seemed
to investigate special cases (spherical or axial symmetry), or approximate solutions. This also was done by
Tonnelat at the end of one of her papers of 1955 [631], and tried again, later, in a dissertation advised by
her [59*]. There, the components of the connection were calculated and compared with the results
of Bonnor [32]. In fact, for high symmetry, the whole work of solving (30*) is unneeded: the
field equations were solved at the same time for both the the metric 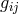 and the connection;
cf. [475].
and the connection;
cf. [475].
A special application refers to Schrödinger’s “star”-connection. In this case, for the skew-symmetric part:
where the bracket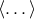 denotes cyclic permutation ([305], p. 745).
denotes cyclic permutation ([305], p. 745).
Remark:
It is interesting to confront Tonnelat’s position with Schrödinger’s. In his paper of 1951, he limited himself to an approximate solution of (30*) by splitting the connection into its symmetrical and skew parts ([558*], Eqs. (1,4), (1,5)):
similarly as M.-A. Tonnelat had done in (361*) and (362*). Equations (368*) and (369*) are more convenient for the setting up of an approximation scheme. In Schrödinger’s words: “ […] from (369*), if the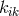 are small, the components of the tensor [torsion] are small of the same order. Hence,
from (368*) the symmetric affinity differs from the Christoffel-brackets only by quantities of the
second order. Thus, using in (369*) the Christoffel-brackets for
are small, the components of the tensor [torsion] are small of the same order. Hence,
from (368*) the symmetric affinity differs from the Christoffel-brackets only by quantities of the
second order. Thus, using in (369*) the Christoffel-brackets for 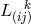 etc., one gets the tensor,
with an error of the third order; and if this is used in (368*), one gets
etc., one gets the tensor,
with an error of the third order; and if this is used in (368*), one gets  with an error of
the fourth order.” From this, “a series of ascending powers of the
with an error of
the fourth order.” From this, “a series of ascending powers of the 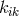 ” can be developed.
Such an approximation up to a certain order, then can be inserted into the remaining field
equations.193
” can be developed.
Such an approximation up to a certain order, then can be inserted into the remaining field
equations.193
10.3 Some further developments
From the mathematical point of view, the results of Tonnelat and Hlavatý may be interpreted as having simplified the study of the weak field equations to some degree. For physics, no new insights were gained. In order to make progress, topics like exact solutions, equations of motion of test particles, or the problem how to express continuously distributed “matter” had to be investigated. It is here that the conflict between the “dualistic” approach to UFT separating the fields and their sources, and the “purely geometric” one showed up clearly. In the latter, the (total) field itself defines its own sources.
10.3.1 Identities, or matter and geometry
As a consequence of the contracted Bianchi-identities, in general relativity the divergence of the
Einstein tensor 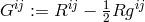 identically vanishes:
identically vanishes: 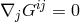 . An implication of the field
equations
. An implication of the field
equations 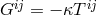 then is the vanishing of the divergence of the so-called “matter” tensor or
energy-momentum-stress tensor of “external” matter, a quantity without geometric significance. In general
relativity,
then is the vanishing of the divergence of the so-called “matter” tensor or
energy-momentum-stress tensor of “external” matter, a quantity without geometric significance. In general
relativity, 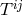 is a functional of the metric, the matter variables, and eventually the connection through
covariant derivatives according to the principle of minimal coupling.
is a functional of the metric, the matter variables, and eventually the connection through
covariant derivatives according to the principle of minimal coupling. 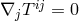 is used to derive
equations of motion for point particles or field equations for matter fields. In UFT, according to
Einstein, no external matter is allowed to occur; matter variables are to be defined from within the
geometry.194
Hence, a distinction between external and internal regions as exemplified by the corresponding
Schwarzschild solutions in general relativity would be unnecessary. In the words of M.-A. Tonnelat:
is used to derive
equations of motion for point particles or field equations for matter fields. In UFT, according to
Einstein, no external matter is allowed to occur; matter variables are to be defined from within the
geometry.194
Hence, a distinction between external and internal regions as exemplified by the corresponding
Schwarzschild solutions in general relativity would be unnecessary. In the words of M.-A. Tonnelat:
“The immediate advantage of a unitary theory is that from the theory itself the form of
the electromagnetic energy-momentum tensor and, perhaps, of the matter tensor can be
extracted. The expression of this tensor then would be imposed by the very geometric
principles, and not by conclusions from an alien theory as interesting as it might be.”
([635*], p. 6)195
An example for an electromagnetic energy-momentum tensor built from geometric quantities is given in (422*) of Section 10.5.4.
As we have seen in Section 9.2, Einstein derived an identity corresponding to the contracted
Bianchi-identity; cf. (260*). It may be rewritten in various forms such as ![∂ [K ˆglk + K ˆgkl − δlK ˆgmn] = 0 l − ik − ki i− mn](article1783x.gif) [409*], or
[409*], or
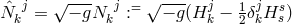 and
and 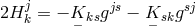 .
.
A reformulation led to
where the Ricci tensor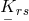 is derived from an arbitrary connection
is derived from an arbitrary connection 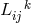 . Expressed by the connection
with vanishing vector torsion
. Expressed by the connection
with vanishing vector torsion 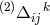 , i.e., after the interchange of
, i.e., after the interchange of 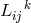 and
and 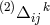 , (372*) remains
formally unchanged for
, (372*) remains
formally unchanged for 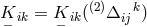 . (372*) can also be expressed as an ordinary divergence:
where
. (372*) can also be expressed as an ordinary divergence:
where 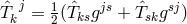 and
and 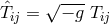 with
with 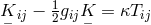 [555, 409], ([632*],
p. 110–113), ([641*], p. 305–308). Expressions for a formal “matter tensor” and an “energy
pseudo-tensor”
[555, 409], ([632*],
p. 110–113), ([641*], p. 305–308). Expressions for a formal “matter tensor” and an “energy
pseudo-tensor” 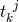 may be read off here (Cf. Eq. (7.22) on p. 113 in [632*]). The procedure is
ambiguous, though, as is known from general relativity. In Mme. Tonnelat’s group, (370*) was named
“identité de conservation” or “conditions de conservation”, and exhibited in several forms. For a
Lagrangian of the form
may be read off here (Cf. Eq. (7.22) on p. 113 in [632*]). The procedure is
ambiguous, though, as is known from general relativity. In Mme. Tonnelat’s group, (370*) was named
“identité de conservation” or “conditions de conservation”, and exhibited in several forms. For a
Lagrangian of the form 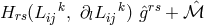 , where the scalar density
, where the scalar density 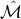 is independent of
the connection
is independent of
the connection 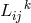 , the “identities of conservation” can be given the form ([359*], p. 89):
For each solution of the corresponding field equations they are identically satisfied.
, the “identities of conservation” can be given the form ([359*], p. 89):
For each solution of the corresponding field equations they are identically satisfied.
In the same spirit, (373*) is often called “conservation law” although the quantity conserved need not correspond to a physical observable. An example of this is given by Kursunŏglu [343*] who chose as his pseudo stress-energy-momentum tensor “beyond the shadow of doubt” to be:
with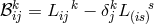 , and
, and 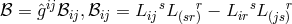 .
. 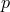 is a constant defined in
Section 9.3.3. Using the notations of Kursunŏglu, Clauser derived what he named contracted Bianchi-Einstein
identity, i.e., (370*):
is a constant defined in
Section 9.3.3. Using the notations of Kursunŏglu, Clauser derived what he named contracted Bianchi-Einstein
identity, i.e., (370*): 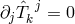 with
with ![ˆTkj = − 2(K (lk)ˆg(lj)) + K [lk]ˆg[lj]) + δ jk (ℬ+K lm ˆglm ) − ℬjlm ˆglm,k − − −](article1809x.gif) . It is
called a “strong” conservation law, because only Eqs. (250*) and (251*) of the weak field equation have been
used, while for a“weak” conservation law all of the weak field equations would be needed [81*].
. It is
called a “strong” conservation law, because only Eqs. (250*) and (251*) of the weak field equation have been
used, while for a“weak” conservation law all of the weak field equations would be needed [81*]. 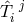 is a
tensor density only with regard to linear coordinate transformations.
is a
tensor density only with regard to linear coordinate transformations.
Another approach for the introduction of the energy-momentum tensor of matter 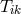 is the following.
First a symmetric metric must be be chosen, e.g.,
is the following.
First a symmetric metric must be be chosen, e.g.,  . Then in the symmetrical part of
the Ricci tensor
. Then in the symmetrical part of
the Ricci tensor 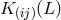 a term of the form of the Einstein tensor
a term of the form of the Einstein tensor 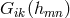 is separated
out. The field equations of UFT are then re-written as formal field equations of the type of
Einstein’s equations in general relativity plus terms left over. This remainder is identified as
is separated
out. The field equations of UFT are then re-written as formal field equations of the type of
Einstein’s equations in general relativity plus terms left over. This remainder is identified as
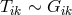 . The method is applicable because mixed geometry can always be re-interpreted as
Riemannian geometry with many extra fields (geometric objects). Its ambiguity lies in the
choice of the Riemannian metric. Taking
. The method is applicable because mixed geometry can always be re-interpreted as
Riemannian geometry with many extra fields (geometric objects). Its ambiguity lies in the
choice of the Riemannian metric. Taking 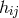 as the metric, or the reciprocal of
as the metric, or the reciprocal of 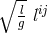 or
or
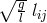 like in [273*, 390*], or another of the many possible choices, makes a difference. By the
formulation within a Riemannian geometry, the unifying strength of a more general geometry is
given up, however. Also, according to a remark by M.-A. Tonnelat, the resulting equations
like in [273*, 390*], or another of the many possible choices, makes a difference. By the
formulation within a Riemannian geometry, the unifying strength of a more general geometry is
given up, however. Also, according to a remark by M.-A. Tonnelat, the resulting equations
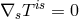 are satisfied identically if
are satisfied identically if  = 0](article1820x.gif) holds. Thus, the information about the
gravitational field contained in the symmetric part of the field equation
holds. Thus, the information about the
gravitational field contained in the symmetric part of the field equation 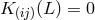 does not
influence the equations of motions of matter following from
does not
influence the equations of motions of matter following from 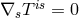 [637*]. Related with this
is the fact that the matter tensor “seems to vanish together with the electromagnetic field
[637*]. Related with this
is the fact that the matter tensor “seems to vanish together with the electromagnetic field
![g[ij]](article1823x.gif) , or at least with a field the properties of which remind of the electromagnetic field” ([635*],
p. 7).196
, or at least with a field the properties of which remind of the electromagnetic field” ([635*],
p. 7).196
In H.-J. Treder’s access to a “matter” tensor in “the asymmetric field theory of Einstein”, the
subtraction was done not on the level of the Einstein tensor, but for the Lagrangian: from
the Lagrangian density of UFT the Einstein Lagrangian was subtracted. An advantage is that
the variational principle ensures the existence of an identity [649*]. A disadvantage is that the
Lagrangian density for the matter part depends not only on the metric but also on its derivatives of
1st and 2nd order. For the metric Treder took the symmetric part 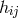 of the asymmetric
fundamental tensor
of the asymmetric
fundamental tensor 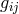 . His references went to Infeld and to Schrödinger’s work, none to
Tonnelat’s. We conclude that Tonnelat’s hope presented in the the first quotation above remained
unfulfilled.
. His references went to Infeld and to Schrödinger’s work, none to
Tonnelat’s. We conclude that Tonnelat’s hope presented in the the first quotation above remained
unfulfilled.
10.3.2 Equations of motion
Unlike in general relativity, in UFT, the equations of motion, in general, are no
longer a direct consequence of the field equations. Ambiguities are bound to
arise.197
A methodological concern was how to properly derive equations of motion for matter, in particular for
point-particles, possibly charged and massive. Two problems arise: In principle, for a single non-interacting
particle certain types of world lines could be defined as paths like the geodesics or auto-parallels in general
relativity. But, what world lines should be investigated, the geodesics of 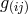 , or of another object chosen
as a representation of the gravitational potential (field)? The geodesics do not depend on
, or of another object chosen
as a representation of the gravitational potential (field)? The geodesics do not depend on ![g[ij] = kij](article1828x.gif) ; in the
usual interpretation of
; in the
usual interpretation of 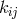 as representing the electromagnetic field, its influence on such paths would be
naught:
as representing the electromagnetic field, its influence on such paths would be
naught:
Secondly, in correspondence to the vacuum field equations of general relativity, the method of treating
the motion of matter as motion of singular point particles as Einstein, Infeld & Hoffmann had done with
their approximation scheme in general relativity (EIH-method) [171, 170], would be in conceptual conflict
with the spirit of UFT. Was it possible, here, to only consider the region outside of a world-tube around the
moving body where the matter tensor 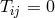 ? The alternative method of Fock with
? The alternative method of Fock with 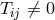 included
the interior of the moving bodies as well. In order to avoid infinitely many degrees of freedom for extended
bodies, some limit procedure had to be introduced. In the EIH-method,
included
the interior of the moving bodies as well. In order to avoid infinitely many degrees of freedom for extended
bodies, some limit procedure had to be introduced. In the EIH-method, 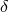 -functions, i.e., distributions are
used as matter sources, although Einstein’s equations do not admit distributions as exact solutions.
Nonetheless, many authors applied the EIH-method also in UFT. E. Clauser showed in great
detail that the method is applicable there for charged particles [83*]; cf. also Section 15. Pham
Tan Hoang wrote his doctoral thesis by applying this “singularity-method” to unified field
theory [273] (cf. Section 10.4.1). However, we have mentioned already in Section 9.3.3 that
both, L. Infeld and J. Callaway were not even able to derive the results of Einstein–Maxwell
theory.
-functions, i.e., distributions are
used as matter sources, although Einstein’s equations do not admit distributions as exact solutions.
Nonetheless, many authors applied the EIH-method also in UFT. E. Clauser showed in great
detail that the method is applicable there for charged particles [83*]; cf. also Section 15. Pham
Tan Hoang wrote his doctoral thesis by applying this “singularity-method” to unified field
theory [273] (cf. Section 10.4.1). However, we have mentioned already in Section 9.3.3 that
both, L. Infeld and J. Callaway were not even able to derive the results of Einstein–Maxwell
theory.
With the singularity-method employed, it turned out to be non-trivial to reach the
Lorentz-force, or even the Coulomb force in a “slow-motion-” and “weak-field-”approximation:
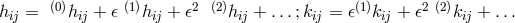 , with only terms
, with only terms 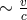 being retained.
In first approximation, only the motion of uncharged particles was described properly by the weak field
equations if
being retained.
In first approximation, only the motion of uncharged particles was described properly by the weak field
equations if 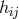 is taken as the metric and
is taken as the metric and 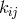 as the electromagnetic field [69*]. This negative result
remained valid up to 4th order in
as the electromagnetic field [69*]. This negative result
remained valid up to 4th order in  for
for 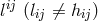 chosen as the metric and
chosen as the metric and 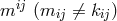 as the
electromagnetic field [271, 272*]. Better results in which the Coulomb force could be made to appear were
achieved by Treder and Clauser [650, 81*, 82*], and later by N. P. Chau, in a slightly changed theory, [77*];
cf. also Section 15.1.
as the
electromagnetic field [271, 272*]. Better results in which the Coulomb force could be made to appear were
achieved by Treder and Clauser [650, 81*, 82*], and later by N. P. Chau, in a slightly changed theory, [77*];
cf. also Section 15.1.
The electric potential is introduced via ![g(2) = 𝜖 ϕ(2) [mn] mns ,s](article1842x.gif) , where
, where 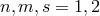 , where
, where ![g(2) [mn ]](article1844x.gif) is the
metric coefficient in the lowest order of an expansion. Here, the equations of motion for two electrical
point-charges
is the
metric coefficient in the lowest order of an expansion. Here, the equations of motion for two electrical
point-charges 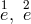 were following from 4th-order equations for the electrostatic potential
were following from 4th-order equations for the electrostatic potential 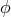 obeying
obeying
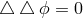
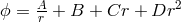 instead of only the Coulomb potential. After the
integration constants
instead of only the Coulomb potential. After the
integration constants 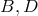 were argued away, the resulting equations of motion turned out to be, for the
first point-charge:
where
were argued away, the resulting equations of motion turned out to be, for the
first point-charge:
where 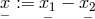 and
and 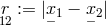 ; underlined letters denote 3-vectors. The constants
; underlined letters denote 3-vectors. The constants
 . are referring to the electric potential of the two charges ([477*], p. 197). However, in
addition to the Coulomb force an unphysical force independent of distance also showed up. It could not be
made to vanish without an accompanying loss of the Coulomb force. In order to remove this defect, the field
equations had to be changed; cf. [77*] and Section 10.4. In Section 9.3.3 we already encountered such an
altered field equation.
. are referring to the electric potential of the two charges ([477*], p. 197). However, in
addition to the Coulomb force an unphysical force independent of distance also showed up. It could not be
made to vanish without an accompanying loss of the Coulomb force. In order to remove this defect, the field
equations had to be changed; cf. [77*] and Section 10.4. In Section 9.3.3 we already encountered such an
altered field equation.
In Section 13.1 we will present Bonnor’s field equations which are leading, in lowest order, to Newton’s
equations for two charges 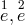 :
:
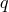 is the ratio of
is the ratio of 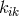 to the electromagnetic field strength, and
to the electromagnetic field strength, and 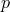 a constant in an additional
term in the Lagrangian. Bonnor ascribed the success due to this added term, quadratic in the
skew-symmetric part of the metric
a constant in an additional
term in the Lagrangian. Bonnor ascribed the success due to this added term, quadratic in the
skew-symmetric part of the metric 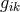 , to the circumstance that “the corresponding terms [in the field
equations] arising from the
, to the circumstance that “the corresponding terms [in the field
equations] arising from the 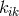 refer not to potentials but to the electromagnetic field strengths.
For this reason it is hardly to be expected that any minor modification of the tensor
refer not to potentials but to the electromagnetic field strengths.
For this reason it is hardly to be expected that any minor modification of the tensor 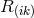 will lead to the Coulomb force” ([33], p. 377). This is also obvious when Bonnor’s term in
the Lagrangian
will lead to the Coulomb force” ([33], p. 377). This is also obvious when Bonnor’s term in
the Lagrangian 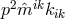 is compared with the usual
is compared with the usual 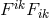 in Maxwell’s theory, because
Bonnor is interpreting
in Maxwell’s theory, because
Bonnor is interpreting 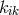 not as an electromagnetic potential but as the electromagnetric field
cf. [35].
not as an electromagnetic potential but as the electromagnetric field
cf. [35].
A. Papapetrou, in a review concerning the problem of motion, pointed out that if Schrödinger’s
equations with a cosmological constant 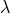 are considered, i.e., Eqs. (236* and (237*), then from
are considered, i.e., Eqs. (236* and (237*), then from
![R {[kl],i} − λg{[kl],i} = 0](article1866x.gif) the equation for the electrostatic potential follows [477*]:
the equation for the electrostatic potential follows [477*]:
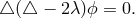
![−2λrA- 2 ϕ ≃ e [r + B + Cr + Dr ]](article1868x.gif) with vanishing
with vanishing 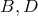 . The constant
. The constant 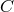 represents electric charge. A
characteristic length
represents electric charge. A
characteristic length 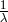 showed up. As Papapetrou wished to apply UFT to elementary particles like the
electron, the problem was that
showed up. As Papapetrou wished to apply UFT to elementary particles like the
electron, the problem was that 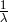 should be of the order of an electron radius and not be of cosmological
significance. His general conclusion was:
should be of the order of an electron radius and not be of cosmological
significance. His general conclusion was:
“It appears impossible to come to a direct phenomenological use of this theory which
would allow a satisfactory treatment of macroscopic problems. But this does not prove
anything with regard to the applicability of the theory in the micro-physical domain.”
([477*], p. 203.)198
A review by M. Lenoir [357] of progress made in the papers by Clauser [81*], Treder [649] and
Papapetrou [477] with regard to the Coulomb force, was reviewed itself by W. B. Bonnor in Mathematical
Reviews [ MR0119977].
MR0119977].
For alternative field equations following from M.-A. Tonnelat’s model cf. (383*) – (385*) in the next Section 10.3.3.
For continuous matter, a third approach within general relativity employed the vanishing of the
covariant divergence of the matter tensor 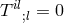 . This assumed a convincing answer to the question of
how to properly define a matter tensor within UFT as described in the previous Section 10.3.1.
M.-A. Tonnelat, in particular, started from the form given to an identity by E. Schrödinger:
. This assumed a convincing answer to the question of
how to properly define a matter tensor within UFT as described in the previous Section 10.3.1.
M.-A. Tonnelat, in particular, started from the form given to an identity by E. Schrödinger:
10.3.3 Tonnelat’s extension of unified field theory
After having spent years of research with Einstein’s Lagrangian 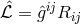 , M.-A. Tonnelat felt confident
that this was not the way to proceed:
, M.-A. Tonnelat felt confident
that this was not the way to proceed:
“Nevertheless, we are convinced that a modification of the generalization of the theory
suggested by Einstein can lead, at least partially, to the goal Einstein himself had set.
[…] if one wants to cling to the original form of this theory which has caused many hopes
and initiated a flood of papers, he would not know how to achieve the objectives which
had been proposed at first, within the strict scope of the theories’ principles.” ([302], p.
117–118)199
Hence she expanded her Lagrangian by including a normed 4-vector ([641*], p. 353):
where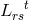 is a connection without vector torsion (
is a connection without vector torsion (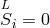 ).
). 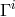 is the new 4-vector (1-form),
is the new 4-vector (1-form), 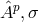 are Lagrangian multipliers, and
are Lagrangian multipliers, and 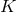 is a constant not to be mixed up with the curvature scalar. For
is a constant not to be mixed up with the curvature scalar. For 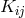 the expression is chosen:
the expression is chosen:
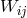 is the Ricci tensor formed with the connection
is the Ricci tensor formed with the connection 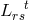 . Note the four additional constant parameters
. Note the four additional constant parameters
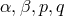 ! In a previous paper of 1960,
! In a previous paper of 1960, 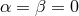 had been assumed [637*]. The ensuing field equations now
were:200
had been assumed [637*]. The ensuing field equations now
were:200
The choice 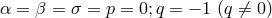 leads back to Einstein’s strong field equations for a
connection without torsion vector. Thus, M.-A. Tonnelat always assumed
leads back to Einstein’s strong field equations for a
connection without torsion vector. Thus, M.-A. Tonnelat always assumed  . The subcase
. The subcase
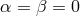 first has been studied by doctoral students of Tonnelat in [361*], and [53*, 56*]. For this case,
(383*) leaves
first has been studied by doctoral students of Tonnelat in [361*], and [53*, 56*]. For this case,
(383*) leaves 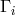 undetermined.
undetermined.
If the Lagrangian density 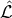 is augmented by a phenomenological matter-Lagrangian density
is augmented by a phenomenological matter-Lagrangian density 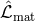 ,
then through
,
then through 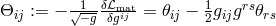 a phenomenological matter-tensor can be
described.
a phenomenological matter-tensor can be
described.
However, it is possible to relinquish the phenomenological matter tensor by using the method of
reformulating mixed or metric-affine geometry as Riemannian geometry. In 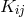 , a Riemannian part
, a Riemannian part
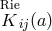 relative to an arbitrarily chosen (symmetric) metric
relative to an arbitrarily chosen (symmetric) metric 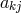 must be exhibited. Eq. (385*) will then
be replaced by
must be exhibited. Eq. (385*) will then
be replaced by
We need not go through all the works similar to the approach in the previous theory of M.-A. Tonnelat, but will only list the following items ([641*], p. 363):
- as a metric, the quantity
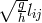 was chosen; 201
was chosen; 201
- geometrically,
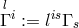 corresponds to vector torsion
corresponds to vector torsion 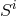 ; physically, according to (384*),
it is linked to the current
; physically, according to (384*),
it is linked to the current 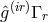 and proportional to the 4-velocity
and proportional to the 4-velocity 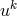 of a particle;
of a particle;
- from the equations of motion, in linear approximation, an acceleration term
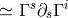 and
the Lorentz force showed up as well as further terms characterizing other forces of unknown
significance.
and
the Lorentz force showed up as well as further terms characterizing other forces of unknown
significance.
The last result needs a comment:
1) As admitted by Tonnelat, it is obtained only after partial neglect of the variational principle: instead
of ![ω[ij] = 0](article1914x.gif) which follows from (386*)
which follows from (386*) ![ω [ij] ⁄= 0](article1915x.gif) must be required in order to give a meaning to an
equation like ([382*], (108), p. 217):
must be required in order to give a meaning to an
equation like ([382*], (108), p. 217):
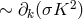 . The covariant
derivative is formed with regard to the Levi-Civita connection for the metric
. The covariant
derivative is formed with regard to the Levi-Civita connection for the metric 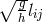 . “Hence,
in the extended version of the asymmetric theory like in the initial version, the equations of
motion can make sense only if at least one of the expressions
. “Hence,
in the extended version of the asymmetric theory like in the initial version, the equations of
motion can make sense only if at least one of the expressions ![ω[ij]](article1919x.gif) or
or ![Θ [ij]](article1920x.gif) does not
vanish.”202
does not
vanish.”202
2) As usual, the equations of motion of charged particles were derived in linear approximation in which
the electromagnetic field 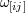 is taken to be small of first order. It was expressed by a vector potential
is taken to be small of first order. It was expressed by a vector potential 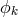 and an axial potential vector through
and an axial potential vector through ![--- χij = √ − l 𝜖ijlm ∂[lχm ]](article1925x.gif) with
with 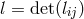 such that:
such that:
![√ --- [l m] kij = g[ij] = 2∂ [iϕj] + − l 𝜖ijlm ∂ χ .](article1927x.gif)
In the end, a simplified version of her extended theory is considered with 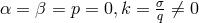 .
The action is
.
The action is
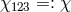 and
and 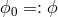 remain203
and satisfy the equations
remain203
and satisfy the equations 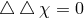 and
and 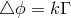 with
with  .
.
10.3.4 Conclusions drawn by M.-A. Tonnelat
In M.-A. Tonnelat’s understanding, Einstein’s unified field theory shows a number of new perspectives:
- the dynamics of both the electromagnetic and the gravitational fields are modified such that there appears to be also an influence of the gravitational field on the electromagnetic one;
- As a nonlinear electrodynamics follows, new effects will appear – as, e.g., “a diffusion of light by light”.
- The relation between field strengths and inductions is similar as in nonlinear Born–Infeld theory ([632*], p. 10.).
She believed that her extension of Einstein’s field equations had alleviated the way toward the equations of motion for charged particles.
Altogether, she seems to have been optimistic about the importance of the theory although
she was aware of the fact that its range of validity was unknown, and many conceptional
questions still remained unanswered. At the time, Mme. Tonnelat’s opinion possibly was
the same as the one ascribed by her to the celebrities: “One may find with Einstein and
Schrödinger a mixture of a certain discourage and of great hopes for the subject.” [632*],
p. 11.)204 Four years later, after progress made had been criticized as irreconcilable with the axioms of UFT, her
attitude still persisted:
Four years later, after progress made had been criticized as irreconcilable with the axioms of UFT, her
attitude still persisted:
“Nevertheless, the discouraging results obtained from different directions never have
definitely compromised the theory; it is the ambiguity of the possible interpretations
(choice of metric, interpretation of the skew-symmetric fields, etc) which have set straight
issues for the inveterate and totalitarian unifiers.” [382*], p. 200).205
The choice of words impregnated by ideology like “inveterate” and “totalitarian” speaks for itself.
As has been remarked before, W. Pauli had criticized unified field theory approached through
metric-affine geometry: he demanded that the fundamental objects must be irreducible with regard to the
permutation group and also referred to Weyl ([487], Anm. 23, p. 273). In this view, an admissible
Lagrangian might be ![ℒ = a ˆg(ik)K (ik) + b ˆg[ik]K [ik]](article1939x.gif) rather than
rather than 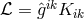 . By an even stricter
application, Pauli’s principle would also rule out this Lagrangian, cf. Section 19.1.1.
. By an even stricter
application, Pauli’s principle would also rule out this Lagrangian, cf. Section 19.1.1.
In 1971, M.-A. Tonnelat veered away from the “unitary spirit” by giving more philosophical comments:
“It would be childish to think that, for Einstein, the existence of the unified fields would
resolve into an ontological criss-cross of torsions and curvatures. It would be likewise
improper to reduce such schemes to a pure formalism without any relation to a universe
the objectivity of which they propose to present. […] The objective pursued by unitary
physics presents itself not as a realization with well defined contours but as a possible
direction. […]” ([645], p. 396)206
10.4 Further work on unified field theory around M.-A. Tonnelat
Much of the work initiated by M.-A. Tonnelat has been realized in doctoral theses, predominantly in the framework of Einstein–Schrödinger field theory. About a dozen will be discussed here. They are concerned with alternative formulations of the field equations, with the identities connected with them, with exact solutions, and with equations of motion for (charged) particles in different approximation schemes.
10.4.1 Research by associates and doctoral students of M.-A. Tonnelat
As to the associates of M.-A. Tonnelat, it is unknown to me how Stamatia Mavridès got into theoretical physics and the group around M.-A. Tonnelat. She had written her doctoral dissertation in 1953 outside of physics [405]. For 5 years, since 1954, she contributed, alone and with Mme. Tonnelat, to Einstein–Schrödinger unitary field theory in many different aspects. Some of her publications have already been encountered. In Section 9.7, her assignment of physical variables to geometrical objects was noted, in Section 10.2.3 her contribution to the removal of the connection. Moreover, her contribution to spherically symmetric exact solutions mentioned in Section 9.6.1 must be kept in mind. Mme. Mavridès also took part in the research on linear field theories; cf. Section 16.1. Since the 1970s, her research interests have turned to astrophysics and cosmology [417].
Judith Winogradzki was a student of L. de Broglie with a thesis on
“the contribution to the theory of physical quantities attached to spin-1/2-particles” [701].
With the topic of her thesis, she easily could have come into contact also with M.-A. Tonnelat.
Although she had shown an interest in affine spaces before writing her dissertation [700], the
concept of spinors permeated her subsequent research even more than unitary field theory. As
noted in Section 9.8, group theory and conservation laws in special relativistic field theories and
general relativity were also dear to her [706]. As was mentioned, she determined the identities
following from Noether’s theorems if applied to the group U (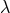 -and coordinate transformations)
and asserted Einstein’s claim that invariance under the group U is able to determine the field
equations207.
Also, Einstein’s
-and coordinate transformations)
and asserted Einstein’s claim that invariance under the group U is able to determine the field
equations207.
Also, Einstein’s 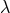 -transformations as an “extension of the relativistic group” were investigated by her
[702]. In another paper, she set out to determine a “gauge”-group, named J-transformations, satisfying:
-transformations as an “extension of the relativistic group” were investigated by her
[702]. In another paper, she set out to determine a “gauge”-group, named J-transformations, satisfying:
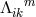 does not depend on the connection L; transposition symmetry is also excluded from (390*). A
variational principle with Lagrangian density
does not depend on the connection L; transposition symmetry is also excluded from (390*). A
variational principle with Lagrangian density 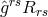 is considered where
is considered where 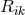 can equal
can equal 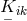 or
or 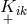 .
J. Winogradzki then proved that
.
J. Winogradzki then proved that  , is necessary, e.g., Einstein’s
, is necessary, e.g., Einstein’s 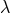 -transformations appear.
The weak field equations of Einstein and Straus are the only ones admitted [703]. Since 1956, no papers on
UFT by her seem to exist.
-transformations appear.
The weak field equations of Einstein and Straus are the only ones admitted [703]. Since 1956, no papers on
UFT by her seem to exist.
We now come to some of the doctoral theses. Jack Lévy’s Lagrangian for unified field theory is a slight generalization of Tonnelat’s: where
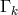 is the torsion vector of the arbitrary (asymmetric) connection
is the torsion vector of the arbitrary (asymmetric) connection 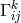 , and
, and 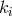 an arbitrary
one-form which can be a function of the arbitrary vector field
an arbitrary
one-form which can be a function of the arbitrary vector field 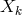 . The third term is introduced “in order
to apply the normalization condition to an arbitrary vector
. The third term is introduced “in order
to apply the normalization condition to an arbitrary vector 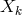 and not necessarily to the torsion vector
and not necessarily to the torsion vector
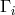 . This is done to avoid any identification or anticipated interpretation of the fields” ([361], p. 249)
208
. This is done to avoid any identification or anticipated interpretation of the fields” ([361], p. 249)
208 Note that in Lévy’s notation
Note that in Lévy’s notation 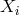 corresponds to
corresponds to 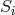 . The field equations follow from variation with
regard to
. The field equations follow from variation with
regard to 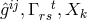 , and the Lagrange multipliers
, and the Lagrange multipliers 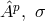 . Among the (weak) field equations,
(235*) is replaced by
. Among the (weak) field equations,
(235*) is replaced by ![[is] 3 gˆ ,s = 2Aˆi](article1964x.gif) which allows the introduction of a non-vanishing electrical
current if
which allows the introduction of a non-vanishing electrical
current if ![ˆg[is]](article1965x.gif) is related to the electromagnetic field (induction). Furthermore, in the field
equations, Lévy put either
is related to the electromagnetic field (induction). Furthermore, in the field
equations, Lévy put either 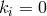 , or
, or 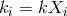 . In the first case the torsion vector drops out,
while
. In the first case the torsion vector drops out,
while  comes in. Also
comes in. Also ![[is] (is) (m ˆg ),s = σˆg Xs](article1969x.gif) with
with  . In the second, the torsion
vector stays and is normed:
. In the second, the torsion
vector stays and is normed: 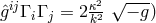 ; furthermore
; furthermore ![[is] σ∕k ˆg ,s = m+2k∕3ˆg(is)Γ s](article1972x.gif) with
with
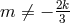 . Lévy then showed that both versions are mathematically and physically equivalent. The
impression here and in the contributions below is that mathematical tricks were played to better
the consistency of the approach without an improvement in the physical understanding of the
theory.
. Lévy then showed that both versions are mathematically and physically equivalent. The
impression here and in the contributions below is that mathematical tricks were played to better
the consistency of the approach without an improvement in the physical understanding of the
theory.
Pham Tan Hoang’s dissertation dealt with equations of motion. First, an explication of the EIH-method for the derivation of such equations for point particles in general relativity, and an introduction into the basics of unified field theory were given [274*]. A useful result by him is the following. A coordinate system defined by
for an affine connection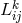 had been named “isothermal” by
M.-A. Tonnelat.209
In general relativity, in linear approximation, (392*) reduces to the coordinate system introduced
for obtaining the wave equation. According to Pham Tan Hoang one can set up a coordinate
system in UFT such that it is also isothermal with regard to the particular Riemannian metric
had been named “isothermal” by
M.-A. Tonnelat.209
In general relativity, in linear approximation, (392*) reduces to the coordinate system introduced
for obtaining the wave equation. According to Pham Tan Hoang one can set up a coordinate
system in UFT such that it is also isothermal with regard to the particular Riemannian metric
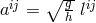 if vector torsion is vanishing. This he ascribes to the relation ([272], p. 67):
Then, Pham Tan Hoang applied the EIH-method to the weak field equations. When
if vector torsion is vanishing. This he ascribes to the relation ([272], p. 67):
Then, Pham Tan Hoang applied the EIH-method to the weak field equations. When 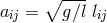 with
with
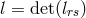 is taken as the metric and
is taken as the metric and 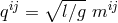 as electromagnetic field, he obtained the same
negative result as J. Callaway [69]: in linear approximation only uncharged particles can be described
properly ([274], p. 89). No cure for this failure was found. In the end, the author could only bemoan the
ambiguity inherent in the basis of the theory – implying structural richness, on the other side. We shall see
that higher approximations had to be calculated in order to get the Coulomb field and the Lorentz force;
cf. Section 15.3. Although dependent on the identifications made, another difficulty pointed out by Pham
Tan Hoang is the vanishing of the charge current with the vanishing of
as electromagnetic field, he obtained the same
negative result as J. Callaway [69]: in linear approximation only uncharged particles can be described
properly ([274], p. 89). No cure for this failure was found. In the end, the author could only bemoan the
ambiguity inherent in the basis of the theory – implying structural richness, on the other side. We shall see
that higher approximations had to be calculated in order to get the Coulomb field and the Lorentz force;
cf. Section 15.3. Although dependent on the identifications made, another difficulty pointed out by Pham
Tan Hoang is the vanishing of the charge current with the vanishing of ![g[ij]](article1981x.gif) . Moreover, the identification
of a geometric object corresponding to the energy-momentum tensor of matter could not be made
unambiguously.
. Moreover, the identification
of a geometric object corresponding to the energy-momentum tensor of matter could not be made
unambiguously.
In her thesis, Liane Bouche-Valere hoped to find acceptable equations of motion for a charged particle by “a method analogous to the one which provides them in the interior electromagnetic case in general relativity.” ([56*], p. 2–3.) By this, we must understand a method working with “conservation conditions”. Her Lagrangian was (up to notation):
where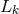 is the torsion-vector of the arbitrary (asymmetric) connection
is the torsion-vector of the arbitrary (asymmetric) connection 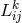 ,
, 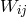 the Ricci tensor
formed from this connection, and
the Ricci tensor
formed from this connection, and 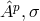 are Lagrangian multipliers.
are Lagrangian multipliers. 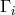 is a normed vector field
[53, 54, 55, 56]. With regard to Tonnelat’s Lagrangian in Section 10.3.3, the terms with constants
is a normed vector field
[53, 54, 55, 56]. With regard to Tonnelat’s Lagrangian in Section 10.3.3, the terms with constants 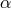 and
and
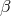 are omitted. L. Bouche demonstrated the existence of 4 characteristic cones, three of which are the
same as in (421*) in Section 10.5.4 below, the 4th was not determined explicitly by her; cf. however the
result of Nguyen Phong-Chau in Section 10.4. Her application of approximations (up to the second one) to
the equations of motion has shown that the Lorentz-force could no longer be obtained as soon as the
antisymmetric part of the field equation was satisfied. Also, her study of spherically symmetric
solutions of the new field equations, due to their complexity could not be carried to a successful
end.
are omitted. L. Bouche demonstrated the existence of 4 characteristic cones, three of which are the
same as in (421*) in Section 10.5.4 below, the 4th was not determined explicitly by her; cf. however the
result of Nguyen Phong-Chau in Section 10.4. Her application of approximations (up to the second one) to
the equations of motion has shown that the Lorentz-force could no longer be obtained as soon as the
antisymmetric part of the field equation was satisfied. Also, her study of spherically symmetric
solutions of the new field equations, due to their complexity could not be carried to a successful
end.
The aim of the thesis by Marcel Bray was to study exact spherically and axially symmetric solutions of
the weak field equations (417*) – (419*) and to compare them with exact solutions in general
relativity.210
For a possible physical interpretation he had to make a choice among differing identifications between
mathematical objects and physical observables. For the metric, interpreted as describing the
inertial-gravitational potentials, he investigated two choices: the metric suggested by Maurer-Tison,
cf. (412*) of Section 9.7, and 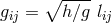 . Unfortunately, his hope that his research “perhaps
could also provide some helpful guiding principles for the choice of the metric” (p. 1) did not
materialize. No solutions of physical interest beyond those already known were displayed by him
[59].
. Unfortunately, his hope that his research “perhaps
could also provide some helpful guiding principles for the choice of the metric” (p. 1) did not
materialize. No solutions of physical interest beyond those already known were displayed by him
[59].
A further systematic study of the possible field equations of Einstein–Schrödinger UFT was done by Nguyen Phong-Chau in his thesis [77, 456*]. He started from a transposition invariant expression for the Ricci tensor with 7 parameters (cf. Section 2.3.2, Eqs. (381*) and (382*)) originally proposed by M.-A. Tonnelat:
where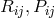 are the two contractions of the curvature tensor of the asymmetric, torsionless affine connection
are the two contractions of the curvature tensor of the asymmetric, torsionless affine connection
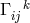 , whereas
, whereas 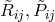 belong to the transposed connection
belong to the transposed connection 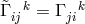 .
.  is an arbitrary vector
field.211
He concluded that only two cases had to be considered: version A of Einstein–Schrödinger with
is an arbitrary vector
field.211
He concluded that only two cases had to be considered: version A of Einstein–Schrödinger with
![Kij = Wij + 2p∂[iΓ j]](article2004x.gif) ; and version B with
; and version B with 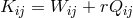 . Here,
. Here, 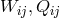 are the contractions of the
curvature tensor belonging to a connection
are the contractions of the
curvature tensor belonging to a connection 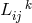 with zero vector torsion while
with zero vector torsion while 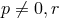 are free
constants. Thus, in version B only 76 (instead of 80) unknown components have to be determined and, for
are free
constants. Thus, in version B only 76 (instead of 80) unknown components have to be determined and, for
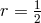 , transposition invariance holds. Nguyen Phong-Chau succeeded in determining explicitly for
arbitrary
, transposition invariance holds. Nguyen Phong-Chau succeeded in determining explicitly for
arbitrary  the fourth characteristic which L. Bouche had announced to exist for case B, but had not
been able to specify in the case
the fourth characteristic which L. Bouche had announced to exist for case B, but had not
been able to specify in the case 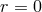 (for the other three cf. (421*) below in Section 10.5.4) :
(for the other three cf. (421*) below in Section 10.5.4) :
It thus seems possible that further linear combinations of the 3 quantities used for the definition of the
“lightcone”, i.e., 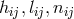 may occur.
may occur.
In the framework of non-linear electromagnetism which should follow from UFT, he suggested an
interpretation different from Maxwell’s theory: the electromagnetic potential ought to be described by a
tensor potential identified with the antisymmetric part of the metric 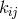 , not just a 4-vector. In first
approximation
, not just a 4-vector. In first
approximation 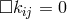 . A consequence would be that elementary particles must be described differently;
beyond mass and charge, an electron would obtain further characteristics incompatible with spherical
symmetry ([456], p. 354).
. A consequence would be that elementary particles must be described differently;
beyond mass and charge, an electron would obtain further characteristics incompatible with spherical
symmetry ([456], p. 354).
Further dissertations dealing with the generalization of Kaluza–Klein theory and with linear theories of gravitation in Minkowski space are discussed in Sections 11.1.1 and 16.1, 16.2, respectively.
10.5 Research by and around André Lichnerowicz
Within the Institut Henri Poincaré, a lively interaction between theoretical physicists, mathematicians and
natural philosophers took place which tried to grab some of the mysteries from “the lap of the gods”. One
of the Paris mathematicians sharing Mme. Tonnelat’s interest in metric affine geometry was André
Lichnerowicz. He looked mainly at
problems of interest for a mathematician. In gravitation – both in general relativity and the “non-symmetric
theory” – questions concerning the integration of the systems of partial differential equations
representing the field equations were investigated, be it identities for curvature, the Cauchy problem
arising from field equations in affine spaces [368*, 370*], existence and uniqueness of solutions and
their global properties, or the compatibility of the field equations of both general relativity
and UFT. In his own words: “[…] I could attack what interested me – the global problems of
relativity, the keys to a real understanding of the theory.” ([379], p. 104.) This has also been
subsumed in Lichnerowicz’s contribution to the Chapel Hill Conference of 1957 on the role of
gravitation re-published in 2011 ([120*], 65–75). For scalar-tensor theory with its 15th scalar variable
 , it is to be noted that Lichnerowicz not only discussed
, it is to be noted that Lichnerowicz not only discussed 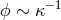 , (
, ( the gravitational
“constant”) as a possibility like Ludwig and Just [385] but accepted this relation right away ([371*],
p. 202).
the gravitational
“constant”) as a possibility like Ludwig and Just [385] but accepted this relation right away ([371*],
p. 202).
10.5.1 Existence of regular solutions?
In Section 7.1, it was pointed out that Einstein thought it imperative to banish singular solutions from his
theory of the total field. Therefore it was important to get some feeling for whether general relativity theory
would allow non-singular solutions or not. Einstein and Pauli set out to prove theorems in this
regard [177*]. Their result was that the vacuum field equation 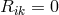 did not admit any
non-singular static solution describing a field with non-vanishing mass. For distances tending to
infinity, the asymptotic values of the Schwarzschild solution were assumed. The proof held for
any dimension of space and thus included the theory by Kaluza and Klein. However, prior to
Einstein and Pauli, Lichnerowicz had proven a theorem almost identical to theirs; he had shown
the non-existence of non-trivial regular stationary, asymptotically Euclidean vacuum solutions
with212
did not admit any
non-singular static solution describing a field with non-vanishing mass. For distances tending to
infinity, the asymptotic values of the Schwarzschild solution were assumed. The proof held for
any dimension of space and thus included the theory by Kaluza and Klein. However, prior to
Einstein and Pauli, Lichnerowicz had proven a theorem almost identical to theirs; he had shown
the non-existence of non-trivial regular stationary, asymptotically Euclidean vacuum solutions
with212
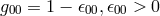 [363, 362, 364]; cf. also Section 8.3. In a letter of 4 September 1945
([489*], p. 309), a double of which he had sent to Einstein, Lichnerowicz pointed this out to
Pauli.213
In his response of 21 September 1945, Pauli found the condition on
[363, 362, 364]; cf. also Section 8.3. In a letter of 4 September 1945
([489*], p. 309), a double of which he had sent to Einstein, Lichnerowicz pointed this out to
Pauli.213
In his response of 21 September 1945, Pauli found the condition on 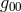 unphysical: why should
unphysical: why should 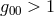 be impossible near infinity? After he had studied the paper of Einstein and Pauli in more detail,
Lichnerowicz commented on it in a further letter to Pauli of 11 November 1945. There, he also confessed to
be “a bit shocked” about the fact that Einstein and Pauli had only proven “non-existence” of regular
solutions while he had shown that Euclidean space is the only regular solution ([489*], p. 325–326). Pauli, in
his answer of 15 November 1945, apparently had suggested a related problem. On 15 December 1945,
Lichnerowicz wrote back that he had solved this problem, outlined the structure of the proof, suggested a
joint publication in Comptes Rendus, and congratulated Pauli for receiving the Nobel prize ([489*],
p. 333–335). A co-authored paper did not appear but Lichnerowicz published a short note: “W. Pauli
signaled me his interest in the possibility to avoid any auxiliary hypothesis: he thought that
this could be reached by a synthesis of our respective methods. In fact, this has happened: an
important problem in relativity theory has been solved” [367]. A further proof of the occurrence of
singularities for static gravitational fields in general relativity was given by A. Lichnerowicz and
Y. Fourès-Bruhat [380]. That Pauli was impressed by Lichnerowicz’s theorem is shown by
his detailed discussion of it in his special lectures on relativity in 1953 as reported in ([194*],
p. 389–390).
be impossible near infinity? After he had studied the paper of Einstein and Pauli in more detail,
Lichnerowicz commented on it in a further letter to Pauli of 11 November 1945. There, he also confessed to
be “a bit shocked” about the fact that Einstein and Pauli had only proven “non-existence” of regular
solutions while he had shown that Euclidean space is the only regular solution ([489*], p. 325–326). Pauli, in
his answer of 15 November 1945, apparently had suggested a related problem. On 15 December 1945,
Lichnerowicz wrote back that he had solved this problem, outlined the structure of the proof, suggested a
joint publication in Comptes Rendus, and congratulated Pauli for receiving the Nobel prize ([489*],
p. 333–335). A co-authored paper did not appear but Lichnerowicz published a short note: “W. Pauli
signaled me his interest in the possibility to avoid any auxiliary hypothesis: he thought that
this could be reached by a synthesis of our respective methods. In fact, this has happened: an
important problem in relativity theory has been solved” [367]. A further proof of the occurrence of
singularities for static gravitational fields in general relativity was given by A. Lichnerowicz and
Y. Fourès-Bruhat [380]. That Pauli was impressed by Lichnerowicz’s theorem is shown by
his detailed discussion of it in his special lectures on relativity in 1953 as reported in ([194*],
p. 389–390).
As already mentioned in Section 8.3, A. Papapetrou, working at the time in Dublin with Schrödinger,
extended the theorem of Einstein and Pauli to a non-symmetric metric, i.e., to UFT with the strong
field equations ![Rik = 0, g ik∥l = 0, ˆg[is],s = 0 +−](article2023x.gif) [474].
[474].
10.5.2 Initial value problem and discontinuities
The field equations for “Einstein’s unitary theory” were presented by A. Lichnerowicz in the form [370*]:
where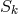 is a covariant vector to be identified with the torsion vector and
is a covariant vector to be identified with the torsion vector and 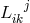 an “a priori arbitrary” affine
connection corresponding to Schrödinger’s star-connection [cf. (291*)]:
an “a priori arbitrary” affine
connection corresponding to Schrödinger’s star-connection [cf. (291*)]: 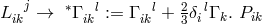 is the Ricci-tensor
is the Ricci-tensor 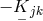 formed from
formed from 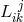 defined by (56*). Note that from (399*) follows
defined by (56*). Note that from (399*) follows
![∂kP [ij] + ∂jP[ki] + ∂iP [jk] = 0](article2030x.gif) , but the reasoning backward holds only locally (local existence of a potential)
([369*], p. 500), ([371*], 267). In Section 10.3.1 , the form given to the generalized Bianchi-identities by
Lichnerowicz is shown.
, but the reasoning backward holds only locally (local existence of a potential)
([369*], p. 500), ([371*], 267). In Section 10.3.1 , the form given to the generalized Bianchi-identities by
Lichnerowicz is shown.
The local initial value problem is the following: Let be given on a spacelike hypersurface
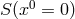 , or
, or 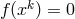 , of the manifold (space-time) the components of the non-symmetric
tensor
, of the manifold (space-time) the components of the non-symmetric
tensor 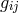 of class (
of class (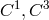 piecewise) and an affine connection of class (
piecewise) and an affine connection of class (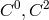 piecewise).214
With (397*) having been solved, i.e., the connection expressed by the metric and its 1st derivatives,
the task now is: Determine in a neighborhood of
piecewise).214
With (397*) having been solved, i.e., the connection expressed by the metric and its 1st derivatives,
the task now is: Determine in a neighborhood of 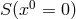 the tensor
the tensor  and the torsion
vector
and the torsion
vector 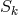 such that they satisfy (398*), (399*). In his main results up to 1954, Lichnerowicz
had shown that the local initial value problem for real and analytical data on
such that they satisfy (398*), (399*). In his main results up to 1954, Lichnerowicz
had shown that the local initial value problem for real and analytical data on 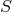 and with
and with
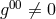 has a unique solution [368*, 370*, 371*], Part II, Chap. VI), [369*]. The proof included a
normalization-condition for the torsion vector:
has a unique solution [368*, 370*, 371*], Part II, Chap. VI), [369*]. The proof included a
normalization-condition for the torsion vector: 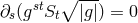 which was also used when in
1955, during the Jubilee-conference in Bern, A. Lichnerowicz reviewed global problems and
theorems “of the relativistic equations”. He now considered part of the field equations given above:
which was also used when in
1955, during the Jubilee-conference in Bern, A. Lichnerowicz reviewed global problems and
theorems “of the relativistic equations”. He now considered part of the field equations given above:
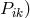
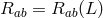 , where
, where 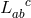 is the torsion-free connection. He
could show that (400*) “presents the same local mathematical coherence as the system of equations of general
relativity”215
is the torsion-free connection. He
could show that (400*) “presents the same local mathematical coherence as the system of equations of general
relativity”215 ([372*], p. 182). The first notice in Comptes Rendus [368*] had been reviewed by V. Hlavatý, and then a
paper by him containing the proofs announced appeared in the journal of Hlavatý’s home university [369].
For the Einstein–Maxwell field equation the requirement that the initial data be analytic had been
weakened by Lichnerowicz’ student, Mme. Fourès-Bruhat, who also gave the first proof of existence and
uniqueness of the local Cauchy problem for Einstein’s field equations [217]. Lichnerowicz conjectured
that such a proof also could be achieved for unitary field theory. Between January and June
1954, a correspondence between Lichnerowicz and Einstein on this topic has taken place; on
11 May 1954 he sent Einstein his paper on the compatibility of the field equations of UFT
[368].216
W. Pauli was impressed by Lichnerowicz’ lecture at the conference in Bern:
([372*], p. 182). The first notice in Comptes Rendus [368*] had been reviewed by V. Hlavatý, and then a
paper by him containing the proofs announced appeared in the journal of Hlavatý’s home university [369].
For the Einstein–Maxwell field equation the requirement that the initial data be analytic had been
weakened by Lichnerowicz’ student, Mme. Fourès-Bruhat, who also gave the first proof of existence and
uniqueness of the local Cauchy problem for Einstein’s field equations [217]. Lichnerowicz conjectured
that such a proof also could be achieved for unitary field theory. Between January and June
1954, a correspondence between Lichnerowicz and Einstein on this topic has taken place; on
11 May 1954 he sent Einstein his paper on the compatibility of the field equations of UFT
[368].216
W. Pauli was impressed by Lichnerowicz’ lecture at the conference in Bern:
“I believe, the most important else we have heard, was the report by Lichnerowicz on the
Cauchy initial value problem in the nonlinear field equations of general relativity. I attach
great importance to the study of such problems, because I suppose that it also will play an
essential role with field quantization.”217 [486].
[486].
Following Hadamard, Lichnerowicz had displayed the discontinuities of the Riemannian
curvature tensor denoted by ![[Rij,rs]](article2047x.gif) on a characteristic
on a characteristic 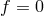 by beginning
with218
by beginning
with218
![i i [∂rLjs] = ujslr, li = ∂if](article2049x.gif) which led to
which led to ![i i i [R j,rs] = lrujs − lsujr](article2050x.gif) . As a consequence,
. As a consequence,
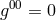 , was in
order.
, was in
order.
In several short notes in Comptes Rendus [291*, 293*, 292, 295*], S. I. Husain applied the methods of A. Lichnerowicz for an investigation of the discontinuities of the curvature and Ricci tensors in mixed geometry, first with Einstein’s “strong” and then the “weak” field equations219. Independently of the field equations, for the discontinuities the expressions of Lichnerowicz hold:
where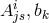 are his discontinuity-parameters and
are his discontinuity-parameters and 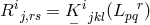 . Thus, (401*) reappeared for the
more general curvature tensor. For the “strong” equations, Husain derived
using
. Thus, (401*) reappeared for the
more general curvature tensor. For the “strong” equations, Husain derived
using 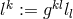 [291]; the 2nd equation is non-trivial because there is no skew symmetry in the
first two indices of the curvature tensor. For the “weak” system, he obtained instead [293]:
In the next paper, he switched to the definition
[291]; the 2nd equation is non-trivial because there is no skew symmetry in the
first two indices of the curvature tensor. For the “weak” system, he obtained instead [293]:
In the next paper, he switched to the definition 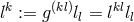 and arrived at
where
and arrived at
where 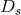 is the covariant derivative with regard to the (Riemann) connection
defined by
is the covariant derivative with regard to the (Riemann) connection
defined by  , and
, and  the curvature tensor belonging to the
connection220
the curvature tensor belonging to the
connection220
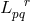 . The congruence-sign in (407*) means “up to terms in
. The congruence-sign in (407*) means “up to terms in ![[Rij,rs]](article2066x.gif) ”. In a further paper, Husain obtained
even
”. In a further paper, Husain obtained
even ![lsDs [P mjil] ≃ 0](article2067x.gif) and concluded that the wave front of radiation propagates “with the fundamental
speed” [295].
and concluded that the wave front of radiation propagates “with the fundamental
speed” [295].
10.5.3 Characteristic surfaces
The propagation of waves with their characteristic surfaces was of great interest also in Einstein–Schrödinger
theory. A naive mathematical approach would take 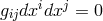 as the defining relation for the
characteristic surface. However, from the point of view of physics, what is the “lightcone” of the
gravitational field? This obviously depends on the identification of the gravitational potential (field) with a
geometric object of unitary field theory. As we have seen in Section 9.7, different identifications were made.
The hypersurface
as the defining relation for the
characteristic surface. However, from the point of view of physics, what is the “lightcone” of the
gravitational field? This obviously depends on the identification of the gravitational potential (field) with a
geometric object of unitary field theory. As we have seen in Section 9.7, different identifications were made.
The hypersurface  represented by
represented by  and tangent to the cone
and tangent to the cone
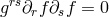 is a wave surface of the metric field
is a wave surface of the metric field 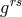 . We already noted that Lichnerowicz preferred
the inverse of
. We already noted that Lichnerowicz preferred
the inverse of 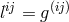 as the “gravitational tensor” and thus defined the light cone through
as the “gravitational tensor” and thus defined the light cone through
In view of the many possibilities of identifying a geometric object with the gravitational field, it
can be understood why V. Hlavatý [260*] and E. Clauser [80] did not follow the approach by
Lichnerowicz. They used the inverse of 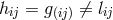 for the definition of the wave fronts:
for the definition of the wave fronts:
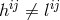 . Clauser dealt with a special case of Hlavatý’s classification with
connection:
where
. Clauser dealt with a special case of Hlavatý’s classification with
connection:
where 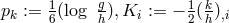 ,
, 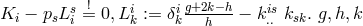 are the
determinants of the corresponding tensors. Indices are moved with
are the
determinants of the corresponding tensors. Indices are moved with 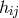 ; the original spot of an index is
noted by a dot. Clauser then was able to show that for the system:
the initial value problem is well defined and the characteristic surfaces are given by (409*).
; the original spot of an index is
noted by a dot. Clauser then was able to show that for the system:
the initial value problem is well defined and the characteristic surfaces are given by (409*).
An important achievement was reached by Françoise Maurer-Tison who continued the
investigation of Lichnerowicz. She pointed out that the characteristic cone of the metric (“light
cone”), locally, can be decomposed into two cones described by the metrics 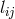 and
and 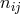 with
with
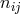 as a further possibility for the metric; cf. [408], ([398*],
p. 243–244), ([641*], p. 339–344). In principle as many “light cones” as different interpretations made for the
gravitational field can be found. However, in the literature studied, we will meet four different light cones
being discussed; cf. also (421*) and (396*).
as a further possibility for the metric; cf. [408], ([398*],
p. 243–244), ([641*], p. 339–344). In principle as many “light cones” as different interpretations made for the
gravitational field can be found. However, in the literature studied, we will meet four different light cones
being discussed; cf. also (421*) and (396*).
When two further approaches to the discontinuities of curvature tensors within the framework of UFT were published in 1961 in Comptes Rendus, the respective authors did not take notice of each other. In the first half of the year, L. Mas and A. Montserrat presented their three papers on “wave fronts” in unified field theory, while in the second half J. Vaillant published on “discontinuities” of the curvature tensor in Einstein–Schrödinger theory. Both continued the work of Lichnerowicz and Maurer-Tison.
In their first paper [390], Mas and Montserrat used the “compatibility equation” (33*) in the form:
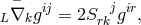
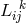 and introduced two further connections
and introduced two further connections  and the
Riemannian connection obtained from
and the
Riemannian connection obtained from 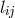 named
named 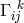 . They referred to Husain’s doctoral thesis [294]
and like him called
. They referred to Husain’s doctoral thesis [294]
and like him called 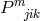 the curvature tensor belonging to
the curvature tensor belonging to 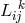 . (405*) and the second equation of (406*)
were reproduced, and the equation for the discontinuities of the Ricci tensor
. (405*) and the second equation of (406*)
were reproduced, and the equation for the discontinuities of the Ricci tensor ![[Pij] = 0](article2095x.gif) added. For the
curvature tensor
added. For the
curvature tensor 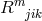 belonging to
belonging to 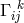 , the results of Lichnerowicz (401*) and the first
equation of (402*) as well as
, the results of Lichnerowicz (401*) and the first
equation of (402*) as well as ![[Rij ] = 0](article2098x.gif) were shown to hold also in the case of Einstein’s weak field
equations. In the second paper, the light cone was defined by
were shown to hold also in the case of Einstein’s weak field
equations. In the second paper, the light cone was defined by 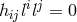 with
with 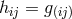 and the
corresponding discontinuities for curvature derived [444]. The third paper then brought an
investigation including three different characteristic surfaces [445]. Let
and the
corresponding discontinuities for curvature derived [444]. The third paper then brought an
investigation including three different characteristic surfaces [445]. Let 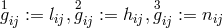 where
where  is defined by (412*), (413*). Then, on the characteristics
is defined by (412*), (413*). Then, on the characteristics  defined by
defined by
 or
or 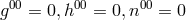 , respectively, for the curvature tensors
, respectively, for the curvature tensors 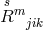 belonging
to the Riemannian connections calculated from
belonging
to the Riemannian connections calculated from 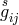 , the following discontinuities obtained:
, the following discontinuities obtained:
In his three notes in Comptes Rendus, Jean Vaillant took up as well the
investigation of the discontinuities of the curvature tensor for the weak field equations
[663*, 664].222
In 1964 he finished his PhD thesis on this and related
subjects.223
For the discontinuities of the curvature tensor on a characteristic, J. Vaillant noted more precisely
![1 pqrs [Pijkl] = 2Kliljη lpkrs(lkhlq − llhkq)](article2109x.gif) . This expression satisfies
. This expression satisfies ![i li[P j,rs] = 0](article2110x.gif) and is consistent with (401*)
and (405*). Vaillant also looked at the characteristics defined from (412*) and by
and is consistent with (401*)
and (405*). Vaillant also looked at the characteristics defined from (412*) and by 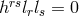 of
F. Maurer-Tison. For both, the discontinuities
of
F. Maurer-Tison. For both, the discontinuities
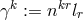 , then also
where the right hand sides contain linear combinations of
, then also
where the right hand sides contain linear combinations of ![i [P j,rs]](article2115x.gif) and
and ![[∇iSj ]](article2116x.gif) , respectively. In his third
paper [665], Vaillant concluded that the only surfaces on which discontinuities of the Ricci tensor can arise,
are the characteristics
, respectively. In his third
paper [665], Vaillant concluded that the only surfaces on which discontinuities of the Ricci tensor can arise,
are the characteristics 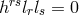 The results of S. I. Husain (cf. Section 10.5.2) were not mentioned by
him.
The results of S. I. Husain (cf. Section 10.5.2) were not mentioned by
him.
10.5.4 Some further work in UFT advised by A. Lichnerowicz
The doctoral theses inspired by A. Lichnerowicz are about equally directed to Einstein–Schrödinger and Jordan–Thiry (Kaluza) theory. As interesting as the study of the Cauchy problem initiated by Lichnerowicz was, it also could not remove the ambiguities in the choice for the metric.
In her thesis “Aspects mathématiques de la théorie du champ unifié d’Einstein–Schrödinger”, Françoise Maurer-Tison first wrote an introductory part on the geometrical background of unified field theory; she developed the concept of “coaffine connection”, i.e., an infinitesimal connection on the fiber bundle of affine reference frames. In Part 2, Maurer-Tison investigated in detail the Cauchy initial value problem. The last Part 3 of her thesis is devoted to the “physical interpretation”.
The “weak” field equations are written in the form:224
where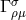 is a linear connection with torsion-vector
is a linear connection with torsion-vector 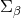 and
and 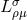 a linear connection with vanishing
torsion vector
a linear connection with vanishing
torsion vector 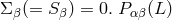 is the Ricci tensor [398*].
is the Ricci tensor [398*].
For the Cauchy initial value problem, (418*), (419*) are rewritten into time-evolution equations
and constraint equations on the initial surface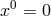 containing
containing ![∂ (g[ρk]√ − g-) = 0 ρ](article2125x.gif) , and an equation for
the Ricci tensor not written down here enclosing the metric, its first derivatives and the vector field
, and an equation for
the Ricci tensor not written down here enclosing the metric, its first derivatives and the vector field
 ([398*], p. 229). The existence of a solution is proven, and, in the case of analytic initial
data, also its uniqueness. There exist three characteristic cones met before and defined by:
where
([398*], p. 229). The existence of a solution is proven, and, in the case of analytic initial
data, also its uniqueness. There exist three characteristic cones met before and defined by:
where 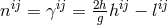 [cf. (412*) and (413*)]. The first one (with
[cf. (412*) and (413*)]. The first one (with  ) is declared to be the light
cone, while the interpretation of the other two (time oriented) as wave fronts remains unclear
(p. 241).
) is declared to be the light
cone, while the interpretation of the other two (time oriented) as wave fronts remains unclear
(p. 241).
In Part 3, after a detailed calculation departing from a proper reformulation of the field equations and the “conservation equations”, Maurer-Tison arrived at what she named energy-momentum tensor of the electromagnetic field:
Electromagnetic field and induction
and induction  are identified as follows:
are identified as follows:
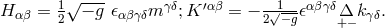 Here,
Here,  is a generalized Laplacian (cf. her
Eq. (40.4) on p. 255). Mme. Maurer-Tison did not only comment in technical terms on her impressive
work; she also described the whole field very much to the point with accurate words:
is a generalized Laplacian (cf. her
Eq. (40.4) on p. 255). Mme. Maurer-Tison did not only comment in technical terms on her impressive
work; she also described the whole field very much to the point with accurate words:
“The unified field theory of Einstein–Schrödinger is attractive by its apparent simplicity
and repellent by the finicky calculations it requires: it is a young theory with moderate
baggage as long as it is investigated with rigour, but an immense load when the efforts are
taken into account which have been tried to explore its possibilities” ([398], p. 187).225
The following doctoral thesis by Marcel Lenoir constitutes a link with the next Section 11.1. In it, he
gave as his aim the introduction of a geometrical structure which permits the incorporation of Bonnor’s
supplementary term into the Lagrangian of UFT (cf. Section 13.1) resulting from the contraction of a
suitable Ricci tensor ([359*], p. 7). This is achieved by the introduction of space-time as a hypersurface of a
5-dimensional space  with metric tensor and asymmetric linear connection. The wanted supplementary
terms follow from the curvature of
with metric tensor and asymmetric linear connection. The wanted supplementary
terms follow from the curvature of  . Lenoir’s approach to Bonnor’s field equations is an alternative to
(and perhaps more convincing) than the earlier derivation, in space-time, by F. de Simoni
(cf. Section 15.1).
. Lenoir’s approach to Bonnor’s field equations is an alternative to
(and perhaps more convincing) than the earlier derivation, in space-time, by F. de Simoni
(cf. Section 15.1).
For a background, in the first two chapters of the thesis, the geometry of fiber bundles and of hypersurfaces was summed up. Lenoir stated the “weak” field equations in the form:
Following Kichenassamy, he distinguished UFT’s of “type Einstein–Schrödinger” with![[is] ∂sˆg = 0](article2138x.gif) and of
type “Einstein–Tonnelat” with
and of
type “Einstein–Tonnelat” with ![∂sˆg[is] = ˆFi ⁄= 0](article2139x.gif) (cf. Section 10.3.3, Eq. (384*)). From an effective
Lagrangian conjured up from the curvature scalar in
(cf. Section 10.3.3, Eq. (384*)). From an effective
Lagrangian conjured up from the curvature scalar in 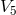 , i.e.,
, i.e.,
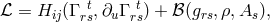
In the last chapter, Lenoir investigated whether Lichnerowicz’s theorem on the non-existence of regular solutions could also be proven for his extended unitary theory but did not arrive at a conclusive result.
The doctoral thesis of another student of Lichnerowicz, Albert Crumeyrolle, contained two different topics [93]. In the larger part, research on the equations of motion of charged particles and on the energy-momentum tensor (corresponding to the “matter” tensor in UFT) was resumed in the framework of Einstein–Schrödinger theory. As to the equations of motion for charged particles, Pham Tan Hoang had simplified calculations by a more complete use of the isothermal condition (392*) and by further improvements as mentioned in Section 10.4. Yet the negative result remained the same as the one already obtained by E. Clauser and H.-J. Treder, cf. Section 10.3.2. The same applies to Crumeyrolle’s approximative calculation of the equations of motions in ([94*], p. 390).
Because the energy-momentum tensor he constructed had to contain a metric field, Crumeyrolle
investigated which of the three possibilities for the metric, i.e., 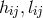 , and
, and 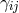 emerging from the
Cauchy-problem (cf. (421*) of Section 10.5.4) would be best for reaching the special relativistic
energy-momentum tensor of the electromagnetic field. In fact, none was good enough. In first
approximation,
emerging from the
Cauchy-problem (cf. (421*) of Section 10.5.4) would be best for reaching the special relativistic
energy-momentum tensor of the electromagnetic field. In fact, none was good enough. In first
approximation, 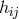 fared best [94*].
fared best [94*].
In the 2nd part of his thesis, an 8-dimensional auxiliary space was introduced
in order to obtain more possibilities for field variables and (modified) field
equations.226
A. Crumeyrolle provided this space 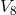 with coordinates
with coordinates 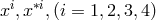 (“natural reference
systems” in comparison with his adapted coordinates
(“natural reference
systems” in comparison with his adapted coordinates 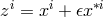 ; cf. Section 2.6); in
; cf. Section 2.6); in 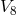 , he
embedded space-time by
, he
embedded space-time by 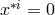 . By use of the covariant derivative
. By use of the covariant derivative  in
in 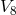 , an affine connection
with parts
, an affine connection
with parts 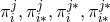 followed. In the special coordinate system, named “natural diagonal reference
system”, projection of the affine connection in
followed. In the special coordinate system, named “natural diagonal reference
system”, projection of the affine connection in 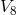 into a 4-dimensional space led to both a connection
into a 4-dimensional space led to both a connection
 , and a tensor
, and a tensor 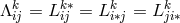 in space-time. Due to the
increase in the number of field variables, he could derive two Ricci-tenors in this 4-dimensional space,
identified with space-time:
in space-time. Due to the
increase in the number of field variables, he could derive two Ricci-tenors in this 4-dimensional space,
identified with space-time:
With these tensors, modified field equations which contained the “weak” Einstein equations including
additional terms in  then could be introduced ([96*], p. 103–128). But a number of extra field
equations had to be joined such as, still among others,
then could be introduced ([96*], p. 103–128). But a number of extra field
equations had to be joined such as, still among others, ![s Λ [sj] = 0,d𝒫¯[jk] = 0, ¯𝒫 (jk) = 0](article2161x.gif) . cf. ([96*], p. 126).
Another approach by Crumeyrolle using a field of numbers different from the real numbers
will be discussed in Section 11.2.2. In its Section XV ([97*], pp. 126–130), it contains a new
attempt at a unified field theory with a slightly changed formalism. As Crumeyrolle’s aim was to
regain the old Einstein–Schrödinger theory from a theory with additional field variables and
field equations, his approach could not bring progress for an eventual physical interpretation of
UFT.
. cf. ([96*], p. 126).
Another approach by Crumeyrolle using a field of numbers different from the real numbers
will be discussed in Section 11.2.2. In its Section XV ([97*], pp. 126–130), it contains a new
attempt at a unified field theory with a slightly changed formalism. As Crumeyrolle’s aim was to
regain the old Einstein–Schrödinger theory from a theory with additional field variables and
field equations, his approach could not bring progress for an eventual physical interpretation of
UFT.


![K− (jk), K− [jk], (336 ) s s ∂kLsj − ∂jL sk , ∂kSj − ∂jSk (337 )](article1573x.gif)

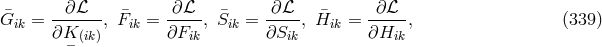
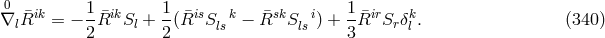

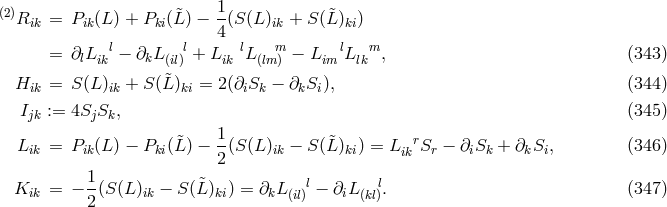

![k k k Lij → L ij + 2δ[iϕj]. (349 )](article1614x.gif)
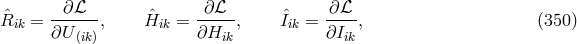




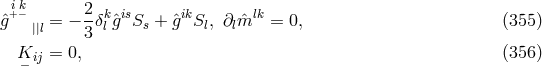
![D gik = 0, ∂ ˆmlk = 0, (357 ) l l K (ij) = 0 ,∂kK [ij] + ∂jK [ki] + ∂iK [jk] = 0. (358 ) − − − −](article1700x.gif)
![gij,k + gik,j − gjk,i − 2gjlL[ikl] − 2gklL [jli] − 2gilL (klj) = 0. (359 )](article1711x.gif)

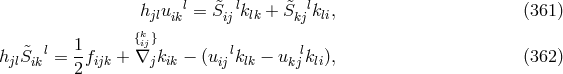


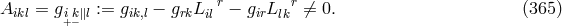

![∗Γ k = k k+ 1hkrk⟨ji||r⟩, (367 ) [ij] ij||0 2 0](article1771x.gif)
![L k= {k}h − hkr (kjsL s+ kisL s) = {k}h − hkr (kjsS s+ kisS s), (368 ) (ij) ij [ir] [jr] ij ir jr L k= S k= 1hkr (k + k + k ) + hkr (k L s− k L s ), (369 ) [ij] ij 2 ir,j rj,i ij,r js (ir) is (jr)](article1773x.gif)
![∂l(K (ik)ˆg(lk)) − K (mn),iˆg(mn ) − ˆg [lm]K {[lm ],i} = 0, (370 ) − − −](article1784x.gif)



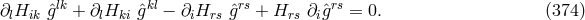
![j --1-- (sj) 1- j (rs) [sj] 1- j [rs] 1- rs j j 𝒯i = 4πp2 {(ˆg K− (si) − 2 δiˆg K− (rs)) − (ˆg K− [si] − 2 δigˆ K− [rs]) + 2(ˆg ,iℬrs− δiℬ )}, (375 )](article1804x.gif)


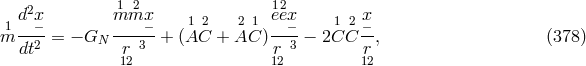

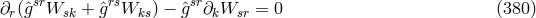
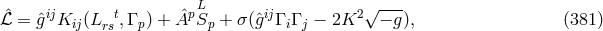
![r r p Kij = Wij + α(∂iL(jr) − ∂jL (ir) ) + 2q∂[iΓ j] + p Γ iΓ j + 2β(∂(iΓ j) − L ij Γ p). (382 )](article1883x.gif)
![−ij+ 2 2 α j 2β j ˆg ∥k = − --δik∂sˆg[js] −---(δik∂sˆg[js] + δk∂sgˆ[is]) − 2βˆgijΓ k +--(δikˆgsj + δkˆgis)Γ s, (383 ) 3 3 3 2 {q + 5-β(1 + 2α)} ∂ ˆg[is] = (4β--− p − σ )ˆg(is)Γ , (384 ) 3 s 3 s ωij := Kij + σ(Γ iΓ j − K2gij ) − 𝜃ij = 0. (385 )](article1892x.gif)
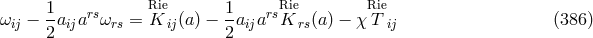
![∘ -- 1 g [rs] Rie [rs] -- --g ω{[ir],s} + ω[ir]∇ sg = 0. (387 ) 2 h](article1916x.gif)
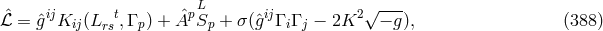
![Kij = Wij + 2q ∂[iΓ j]. (389 )](article1930x.gif)
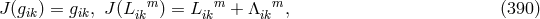
![√ --- ˆℒ = [ˆgijKij(Γrst ) + 2mX [i,j]] + 2Aˆp (Γ p − kp) + σ (ˆgijXiXj − 2κ2 − g), (391 )](article1951x.gif)


![√ --- ℒˆ = ˆgij[ Wij(L rst) + 2q∂[iΓ j] + p Γ iΓ j ] + AˆkLk + σ(ˆgijΓ iΓ j − 2κ2 − g), (394 )](article1982x.gif)
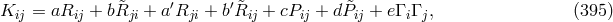
![i j 4- [(1 + 𝜖)hij − lij]dx dx = 0, 𝜖 = − 1 + 3r(r − 1),𝜖 ⁄= 0. (396 )](article2012x.gif)
![r r g+ik−∥l := gik,l − grkLil − girLlk = 0, (397 ) [is] ˆg ,s = 0, (398 ) 4- Pik = 3 ∂[iSk], (399 )](article2024x.gif)
![2 ∘ --- Rab − --(∂aSb − ∂bSa) = 0, ∂s(g[sa] |g|) = 0, (400 ) 3](article2043x.gif)
![i i i lk[R j,rs] + ls[R j,kr] + lr[R j,sk] = 0, (401 )](article2051x.gif)
![q r i lq[R j,rs] = 0, l [R p,rs] = 0. (402 )](article2052x.gif)
![[Rij,rs] = lrAijs − lsAijr, [∂jSk ] = ljbk, li = ∂if, (403 )](article2054x.gif)
![lq[Rqj,rs] = 0, lp[Rip,rs] = 0, (404 )](article2057x.gif)
![q i p i lq[R j,rs]l = l[R p,rs] lj. (405 )](article2059x.gif)
![s m m m l Dsli = 0, li[P jkl] + ll[P jik] + lk[P jli] = 0, (406 ) 2lsDs [P mjil] + ll[DsP mjsi] + li[DsP mjls] ≃ 0, (407 )](article2061x.gif)


![k k 1 ks h h h ks s k s k s k Γij = {ij}h + 2-h (∇igsj + ∇jgis + ∇sgij) + 2ps(gijh + 2k.[iδj] + k .[jδi] − δ.(iδj)), (410 )](article2078x.gif)
![R = 0, R = 0, ∇ (K − p Ls) = 0 (411 ) (ij) [ij] k i s i](article2082x.gif)
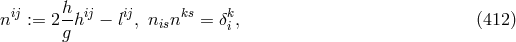

![s s s s lk[Rij,rt] + lt[Rij,kr] + lr[Rij,tk] = 0, lt[Rij,tk] = 0. (414 )](article2108x.gif)
![li[Pmjkl] + ll[Pmjik] + lk[Pmjli] = 0, lr[Pip,rs] = 0 , li[Pip,rs] = 0 (415 )](article2112x.gif)
![γp∇p [P ij,rs] ≃ 0, γp∇p [∂jSk ] ≃ 0, (416 )](article2114x.gif)
![σ σ ∂ρgλμ − Lλρgσμ − Lρμgλσ = 0, (417 ) ∂ (g[ρβ]√ − g) = 0, (418 ) ρ Pαβ − 2-(∂αΣ β − ∂ βΣα) = 0, (419 ) 3](article2118x.gif)
![∂ (g[k0]√ −-g) = 0, P − 2-(∂Σ − ∂ Σ ) = 0 (i,k = 1,2,3), (420 ) k i0 3 i 0 0 i](article2123x.gif)
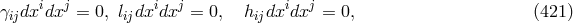
![τλμ = P[λσ]m ρσhρμ + P[μσ]m ρσh λρ − 1-hλμP [αβ]mα β. (422 ) 2](article2130x.gif)
![i− j+ ij ij s is j sj i ij 2- i js ˆg ∥k(= ∂kˆg − ˆg Γks + ˆg Γks + ˆg Γsk ) = gˆ Γ k − 3 δkˆg Γ s, (423 ) [is] ∂sˆg = 0, (424 ) Kij = 0. (425 )](article2137x.gif)