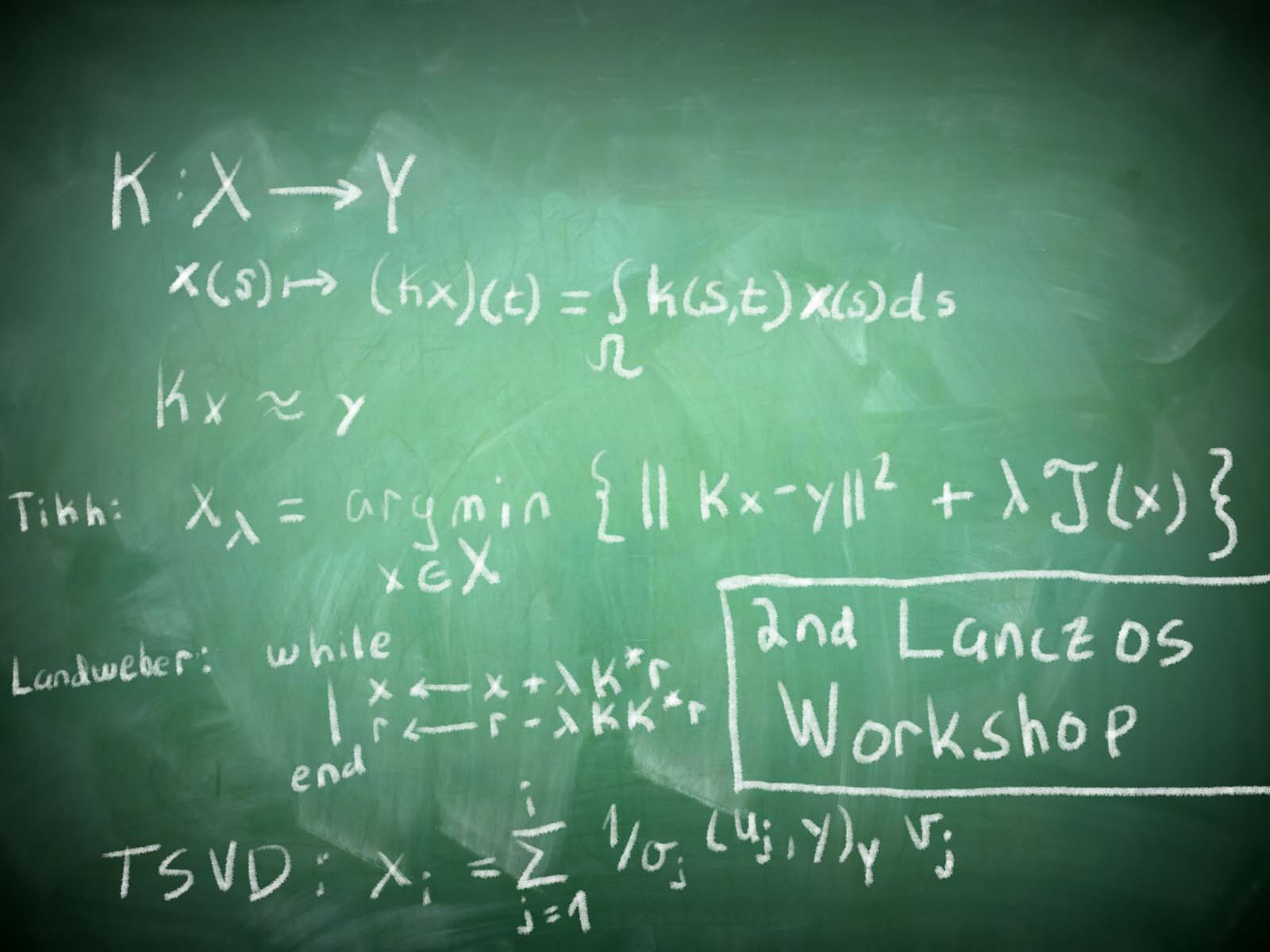
The application of state-of-the-art iterative methods for the treatment of inverse problems is an active field of research in applied/computational mathematics at the intersection of numerical analysis and applied analysis. The tools of numerical analysis have enabled the fast and efficient solution of a range of problems from crucial real-world applications. The tools of applied analysis have been used to deliver convergence and stability results in the continuum setting. However, these two bodies of literature do not always interact.
This workshop considerings both of these approaches to encourage greater interaction of researchers from both communities, specifically targetting younger researchers. This workshop will combine introductory lectures on interrelated subtopics, such as iterative methods in continuum problems and large-scale discrete ill-posed problems.
Register to participate now. Note that there is no registration fee. The deadline for registration to apply to present a short talk or poster is 24 March 2022.

Early-career researchers and postdocs are invited to apply to present their work in short talks.
Students are invited to apply to present their work in a poster session.

A short course will be given on the Matlab package for large-scale descrete ill-posed problems IR-Tools
The workshop will take place from the 26th to the 30th of April 2022. The posted schedule is preliminary.
The poster session will begin with a raucous poster blitz after which the poster presenters will retreat to their posters and workshop participants will be able to visit the posters and discuss the presenters' research with them.
Bernadett StadlerJohannes Kepler University Linz |
Simon WilsonTrinity College Dublin |
Jiahua JiangUniversity of Birmingham |
Salla-Maaria Latva-ÄijöUniversity of Helsinki |
Dung PhamTrinity College Dublin |
Siiri RautioUniversity of Helsinki |
Nikolaos PetropoulosUniversity College Dublin |
Zhi-Zhen WangTrinity College Dublin |
Alexander MeaneyUniversity of Helsinki |
Lukas VierusSaarland University |
Caelen FellerTrinity College Dublin |
Elli KarvonenUniversity of Helsinki |
Fabian HintererJohannes Kepler University Linz |
Otmar ScherzerUniversität Wien |
Ronny RamlauKepler Universität Linz |
Silvia GazzolaUniversity of Bath |
Simon HubmerRadon Institute (RICAM) |
Arvind SaibabaNorth Carolina State University |
Eric de SturlerVirginia Tech |
Ekaterina SherinaUniversität Wien |
Biswajit BasuTrinity College Dublin |
Kirk SoodhalterTrinity College Dublin |
Patrick FritzschTrinity College Dublin |
Sinéad RyanTrinity College Dublin |
Liam BurkeTrinity College Dublin |
Kate HavengaTrinity College Dublin |
Edward DonlonTechnological University Dublin |
Prabhav MehraTrinity College Dublin |
Organised by

Scientific Organiser

Local and Scientific Organiser

Scientific Organiser
Prof. Sinéad Ryan
Emma Clancy
Karen O'Doherty
Ciara Scanlon
We look forward to hearing from you!
Dublin, Ireland
ksoodha@maths.tcd.ie