Below you will find some examples of fractals I have drawn in C. The source code for them is based off of Dr Tom Archer's code for writing matrices to pbm format images which I have edited to make colour ppm files, and the three pieces of code needed can be found here, here and here.
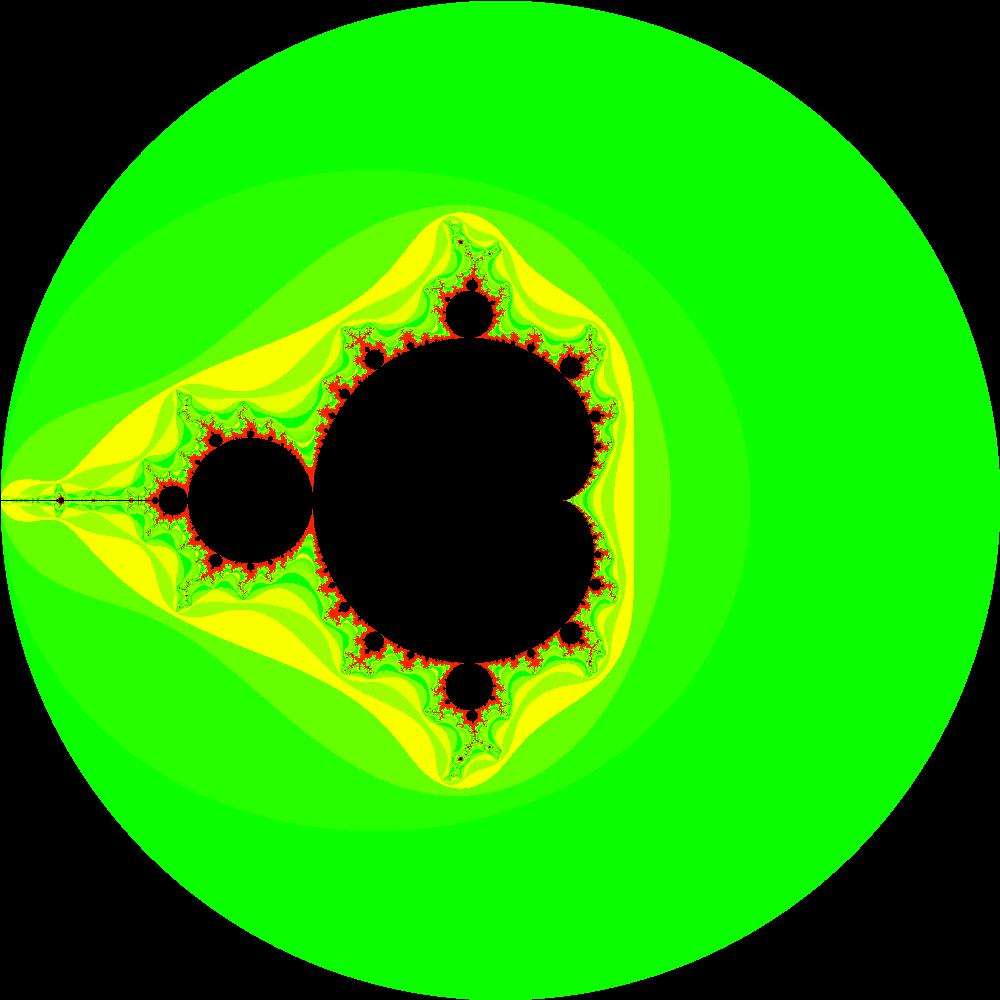
A Mandelbrot Set (shown above), is the set of all complex constants c for which the iterative equation z -> z^2 + c does not diverge for a starting value of complex z = 0. In practice, we use the fact that any point which reaches a radius of 2 or greater will eventually diverge. We colour the points via how many iterations it takes them to escape this radius. The code given is that for a Mandelbrot set, though it can be easily modified to create the following examples.
A simple generalisation of the Mandelbrot set is to change the power in the equation. Below is the case of z -> z^4 + c.

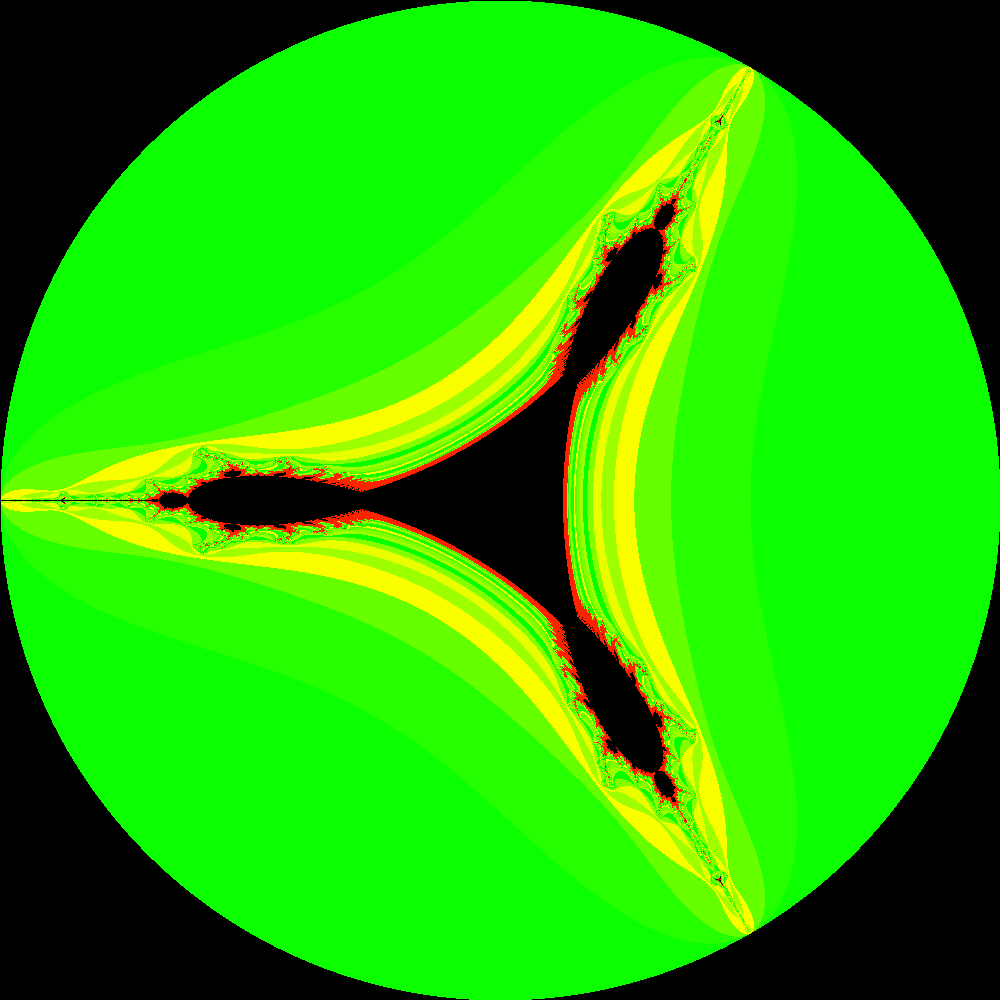
Another interesting case is to consider z -> (z*)^2 + c, which yields the so-called tricorn fractal shown below.
Probably the most intersting variation I have found is the Burning Ship Fractal. This is gotten by take the absolute value of the real and imaginary parts before the iterations, as follows:
(x + iy) -> (|x| +i|y|)^2 + c
This tiny change in the equation produces a set vastly different from the Mandelbrot Set, referred to as its "evil twin":
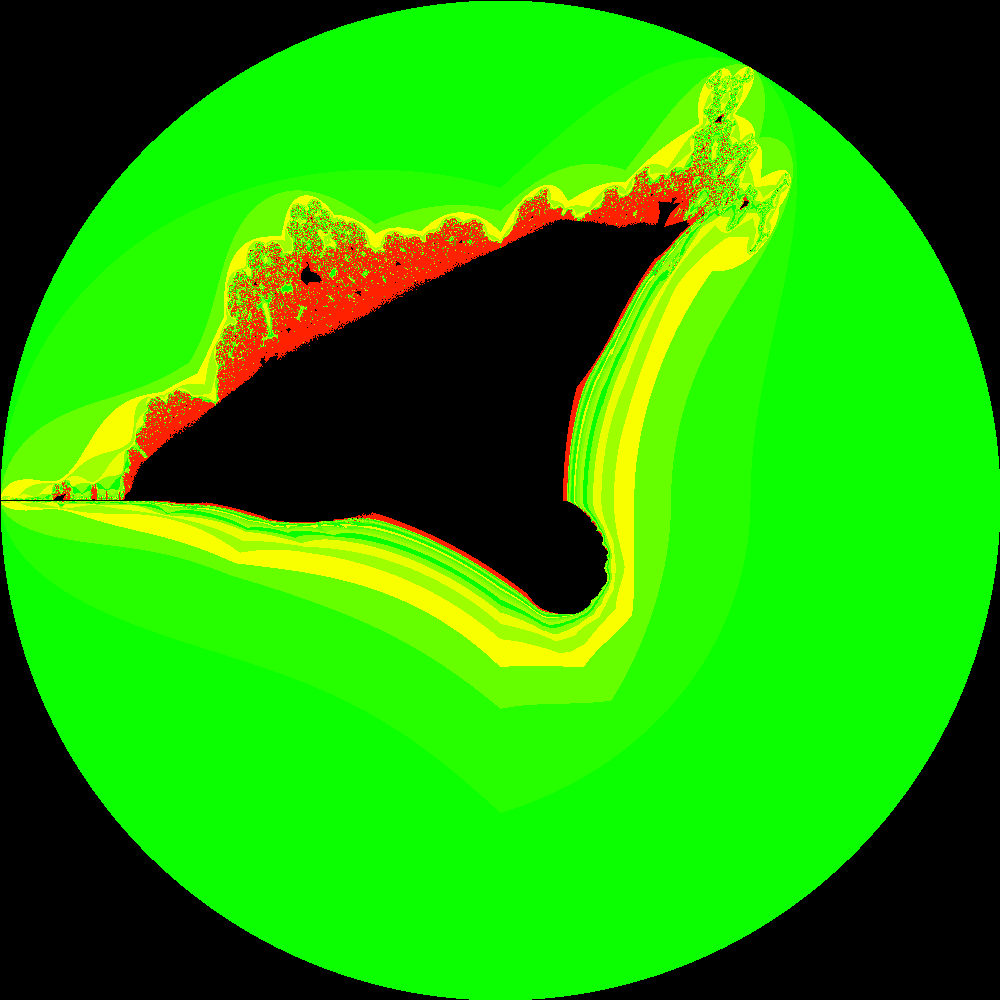
The name of the fractals becomes obvious if we zoom in on the small region in the left of the image, yielding what looks like a cross between a pirate ship on fire and a colosseum.

Another interesting fractal is that of the Collatz Conjecture. The conjecture can be generalised to complex numbers. We then plot the numbers which produce bounded sequences in black, and the unbounded ones coloured according to how long it take them to escape outside of a certain radius.

And here is a zoomed-in region:
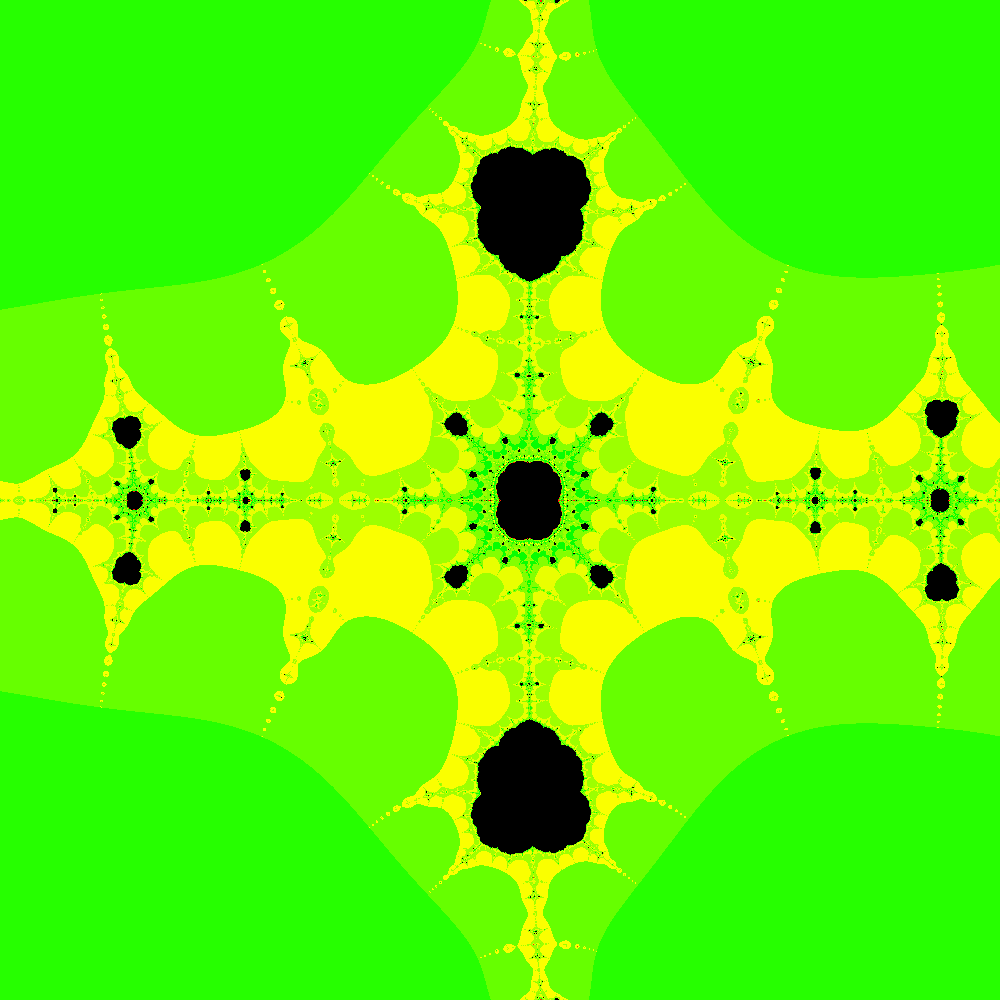
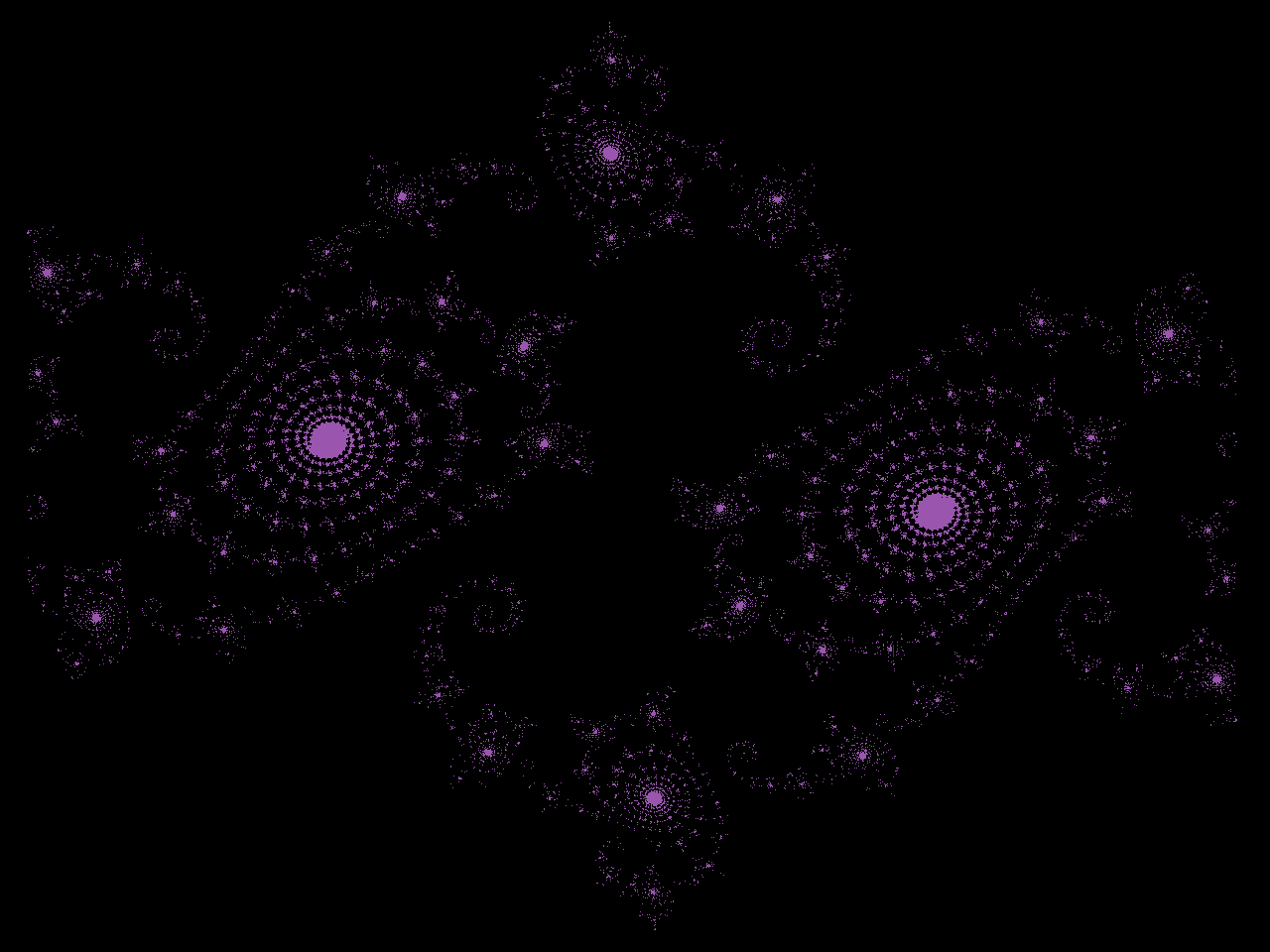
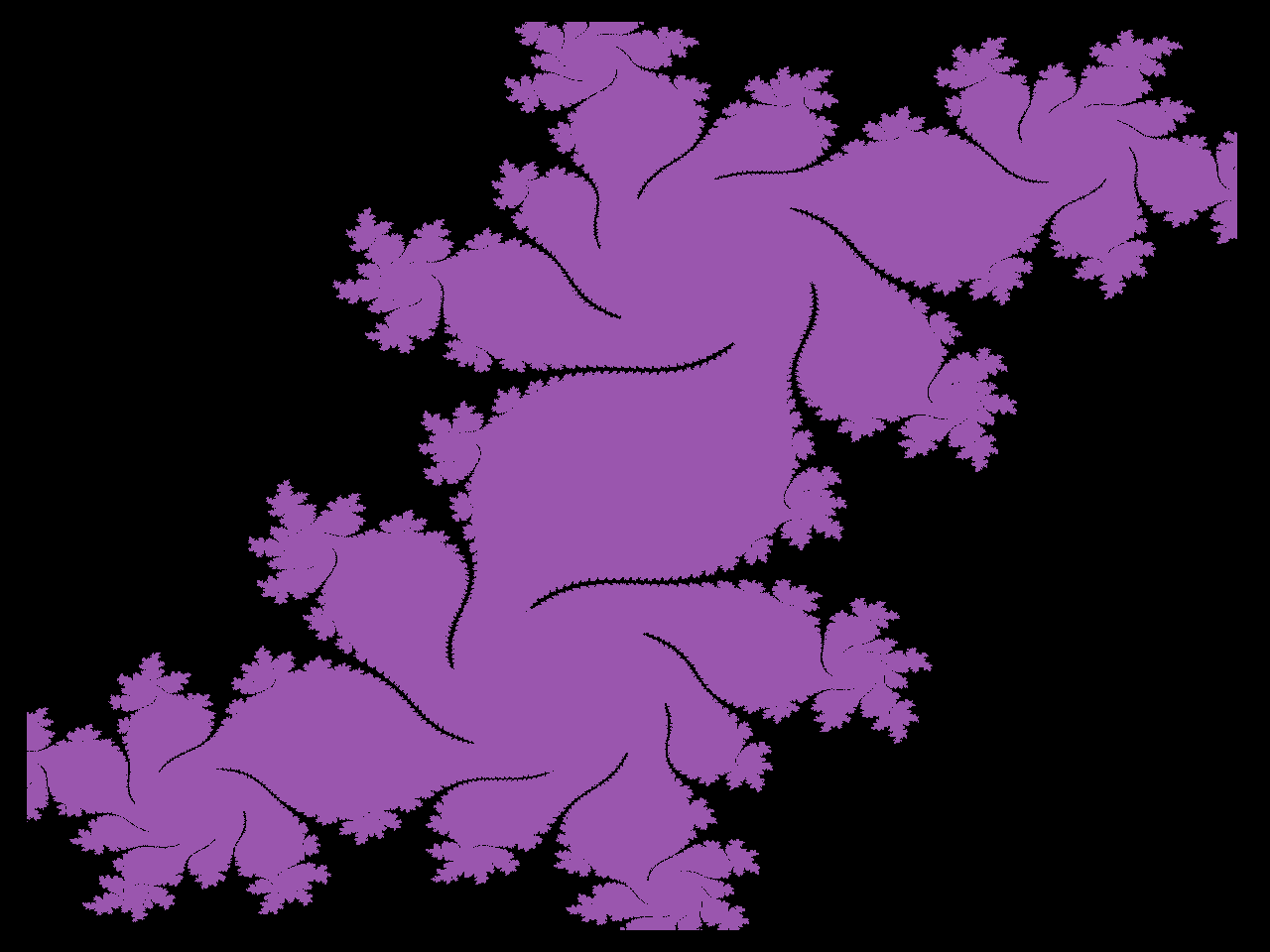
Finally we have Julia Sets. These are sets of the values of z which don't diverge under z -> z^2 + c for a given c. For this I have a different program which I wrote last year, though you could easily modify the previous code to do Julia Sets. The old program can be found here. Below are a few of the more interesting examples I have found.





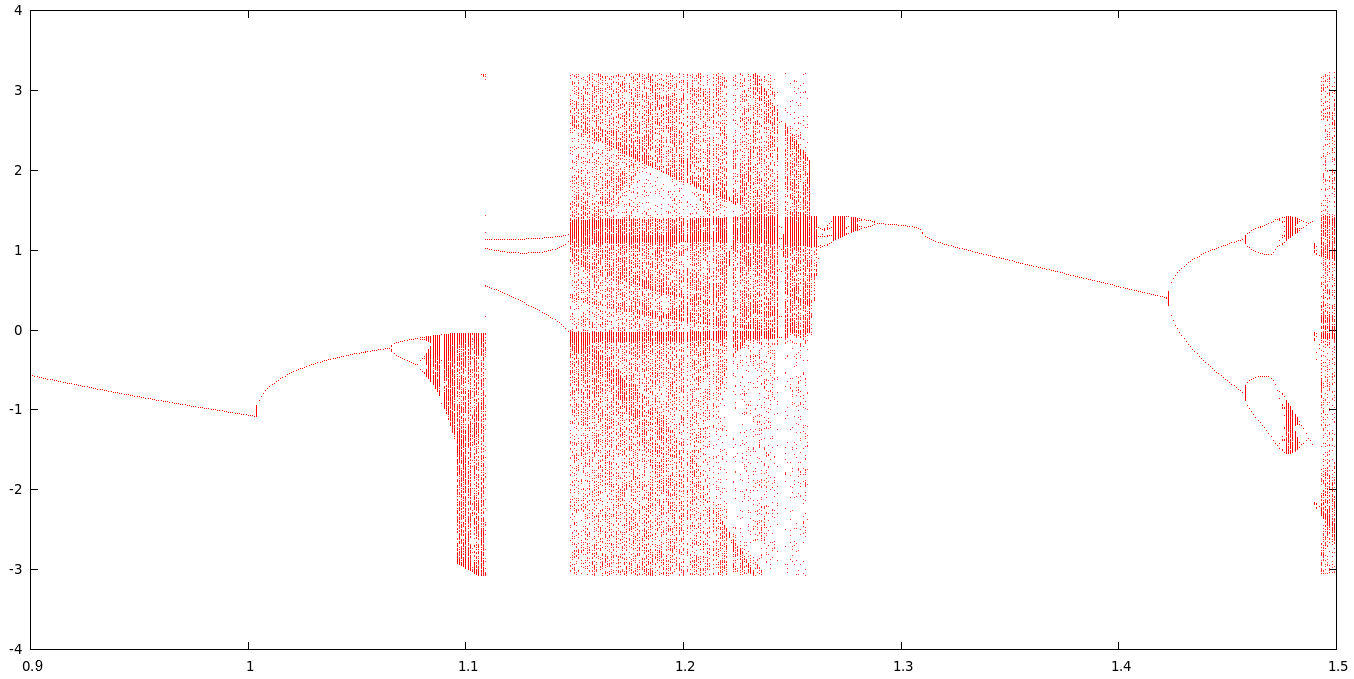
A slightly unrelated but similarly interesting piece of code I have written is that of a bifurcation diagram. In our second year physics computational lab, we were required to write a program to produce phase diagrams for a compound pendulum, a well-known chaotic system. These phase diagrams were all that was required by the lab, but I realised that the information could be summed up in a single bifurcation diagram. I wrote some code in my own time and produced the following diagram, which clearly shows the period doubling and chaotic regions we expect from a compound pendulum.