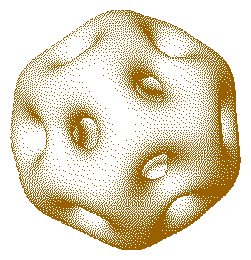
A surface of constant energy density for the 9-Skyrmion, calculated using a mixture of numerical and analytical methods.

This is a short description of my work I wrote for the Irish Scientist Year Book.
In the last century it was fancifully suggested that molecules are knots in the aether. While we now know that there is no aether and that molecules are not the fundamental constituents of matter, the idea that matter has a topological origin remains beautiful and compelling. In recent years theoretical physicists have become excited by the modern formulation of this idea; soliton theory and soliton-particle duality.
Physicists use quantum field theories to describe fundamental particles. These quantum field theories are derived by quantizing classical field theories. Whereas classical field theories describe the dynamics of continuum fields, quantum field theories can be interpreted as describing the interactions of individual particles.
It is a striking feature of some field theories that their classical dynamical equations have particle-like solutions known as solitons. Unlike the particles introduced by the quantization procedure, solitons are germane to the classical, continuum, theory. They owe their particle-like properties, not to quantization, but to the topology of the field theory itself.
If a field theory with solitons is quantized, there will be two different spectra. There is the spectrum of particle-like solitons and the spectrum of the actual particles. Particle-soliton duality is the idea that in certain field theories the two spectra may be inter-related or inter-reliant. This exciting idea has had important applications in super-symmetric field theory and in super-string theory.
The fundamental particle spectrum of a field theory often includes massless gluons. For example, massless gluons are a feature of Quantum Chromo-Dynamics, the quantum theory which describes the strong nuclear force. It is not understood how particle-soliton duality applies to field theories with massless gluons. The classical behavior of these massless solitons is quite mysterious. This is being studied at Trinity, in collaboration with researchers at Columbia University, New York.
Another soliton theory is the Skyrme model. This a very speculative non-linear theory of nuclear interactions which has a very rich mathematical structure. The fundemental particles in the Skyrme model are pions and the solitons, which are called Skyrmions, are classical nuclei.
Skyrmions are surprising and beautiful in shape. The nine-Skyrmion is pictured above, this Skyrmion is a classical beryllium nucleus. Of course, this shape may not survive quantization. However, the classical solutions must be known before the quantized behavior can be understood. These solutions are being studied at Trinity, in collaboration with researchers at Cambridge University and at the University of Kent at Canterbury.