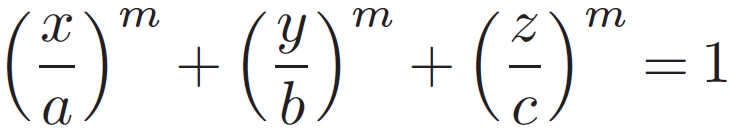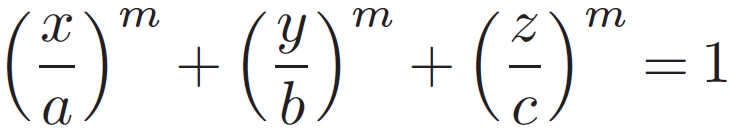Superellipsoids
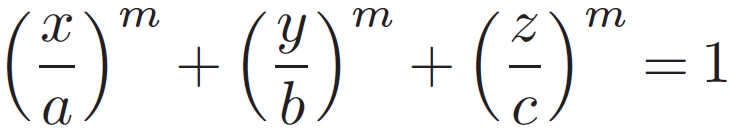

The formula for a superellipsoid is shown above. This is a generalisation of the expression for an ellipsoid. The shapes formed for various biaxial grains (a=b) with aspect ratios &alpha=c/b and shape parameters m are shown on the right.
For m=2 we recover the expression for an ellipsoid. For equiaxed grains (&alpha = 1) we get a progression of "superballs", that range from a sphere (m=2) to a cube (m=&infin). Other shapes that lie between ellipsoids and cuboids are obtained for values of m>2 combined with noninteger values of &alpha .
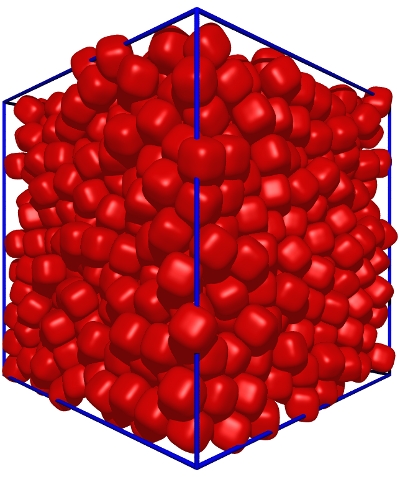
Superball packings
Superballs are equiaxed superellipsoids (a=b=c). Their shape parameter m controls how cubic their shape is, with m=2 corresponding to a sphere and m=&infin a perfect cube. The symmetry due to the equivalence of their 3 axes leads to very interesting packing properties. These shapes show the strongest tendancy to order of all the superellipsoids, in particular at high m values.
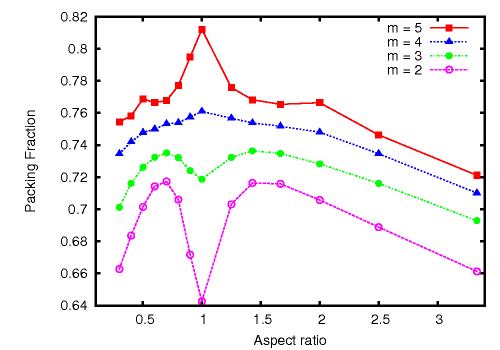
The packing fractions obtained for a set of superball packings with m=2, 3, 4, and 5 are shown in the figure below (these corresponds to an aspect ratio &alpha = 1 on the x-axis). We see that for the case of the sphere, we obtain a random close packing with 64% density. Increasing m causes a rapid increase in the packing fraction, with values around 82% found for m=5.
Details of the structural properties of these packings and an analysis of their orientational ordering are given in our paper [1].
Superellipsoid packings
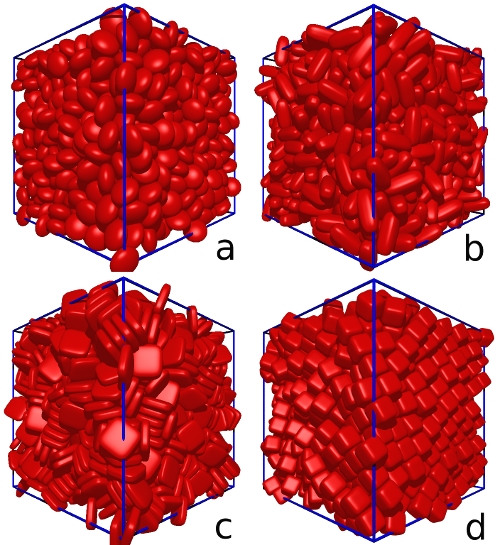
We employ a dynamic particle expansion technique, with the final density and the resulting structural properties of the packings being dependant on the volumetric growth rate used in the simulation. Here we choose a growth rate that generates random close packings of ellipsoids (Fig. a) and then apply that same growth rate to generate packings of superellipsoids. This allows us to compare how the various superellipsoid shapes affect their packing properties.
Two key properties of the grain shape are found to
determine their packing behavior: their degree of anisotropy
(aspect ratio) and their surface curvature. The large regions
of low surface curvature for high m values, readily generate
large amounts of face on face inter-grain contacts and thus
large amounts of orientational ordering.
This can be seen in Figure d and we have quantified it using an orientational order parameter. At high m values (m=4 and m=5),
the densest packings are formed by the superballs (Fig. d), which are the grains with the
highest degree of symmetry (&alpha=1). As we increase the
anisotropy of the grain shape by changing the aspect ratio
away from unity, we see a rapid drop off in the ordering and
the density of the packings falls. Clearly high degrees of
symmetry aid ordering effects and the anisotropy reduces
the ability of a very ordered packing to form, leading
to a decrease in both the density and the orientational
ordering. This is contrary to the behavior at low m values
(m=2 and 3) where predominantly disordered packings
are formed and moderate degrees of anisotropy cause an
increase in packing fraction.
Details of this work are given in our paper The packing properties of superellipsoids
.
References
1. "
The packing properties of superellipsoids",
G.W. Delaney and P.W. Cleary, Europhysics Letters ,
89, 34002, 18 February 2010.
Back to homepage
(Email: gdelaney "AT" gmail "DOT" com)