The Bathtub Curve and Product Failure Behavior
Part Two - Normal Life and Wear-Out
by Dennis J. Wilkins
Retired Hewlett-Packard Senior Reliability Specialist, currently a ReliaSoft Reliability Field Consultant
This paper is adapted with permission from work done while at Hewlett-Packard.
Introduction
Part One of this article (presented in last month's HotWire)
introduced the concept of the reliability bathtub curve. This is a
graphical representation of the lifetime of a population of products,
which consists of three key periods. Part One examined the first period
of the curve, infant mortality, and also discussed issues related to
burn-in, a common practice to reduce the occurrence of this type of
failure during the useful life of the product. Part Two (presented
here) will address the middle and last periods in the bathtub curve:
normal life (or "useful life") and end of life wear-out. The normal
life period is characterized by a low, relatively constant failure rate
with failures that are considered to be random cases of "stress
exceeding strength." The wear-out period is characterized by an
increasing failure rate with failures that are caused by the "wear and
tear" on the product over time.
Reliability Bathtub Curve Review
As described in more detail in Part One, the bathtub curve, displayed in Figure 1 below, does not
depict the failure rate of a single item. Instead, the curve describes
the relative failure rate of an entire population of products over
time. Some individual units will fail relatively early (infant
mortality failures), others (we hope most) will last until wear-out,
and some will fail during the relatively long period typically called
normal life. The first period is characterized by a decreasing failure
rate and consists of failures caused by defects and blunders. The
second period maintains a low and relatively constant failure rate and
consists of random failures typically caused by "stress exceeding
strength." The third period exhibits an increasing failure rate and
consists of failures caused by wear-out due to fatigue or depletion of
materials.
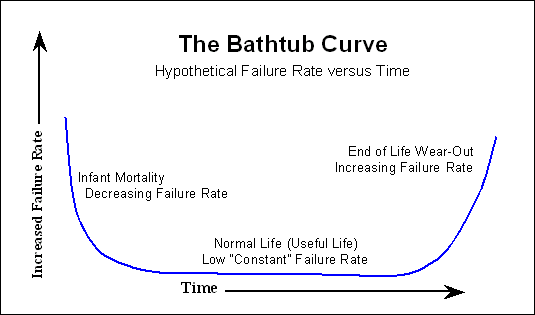
Figure 1: The Bathtub Curve
Normal Life Period – Does it Really Exist?
Some reliability specialists like to point out that real products don't
exhibit constant failure rates. This is quite true for a mechanical
part where wear-out is the primary failure mode. And all kinds of
parts, mechanical and electronic, are subject to infant mortality
failures from intrinsic defects. But there are common situations where
a true random failure potential exists.
Soft
Error Rate (SER) is a fact of life for systems using solid state memory
chips. And today that includes about any electronic device, from a
personal computer to a VCR, microwave oven, digital camera or
automotive control module. These errors are caused by two factors:
alpha particles and cosmic rays. These errors are random in time and
transient. A bit that is "flipped" by one of these factors will be
corrected when new data is written to the same memory cell. But if that
cell is read before a new write operation takes place, the data read
will be erroneous. The effect of the error may be minor (such as a
single pixel of a display being the wrong color for one screen refresh
cycle) or major (such as crashing a PC). In business-critical computer
systems, special error correcting codes are employed to prevent SER
from causing any data loss or system malfunctions. However, most
electronic products will malfunction in some way from SER.
For
SER, the failure mode is a normal life failure. There is an average
rate of occurrence but the failures occur "at random." The failures in
most cases cause only a minor deviation in operation and are
self-correcting. No repair is needed to "fix" a product subject to SER
and, in fact, no "fix" can eliminate SER effects. Only a significant
design change (using an error correcting design) can eliminate the effects of SER, but nothing can eliminate SER.
There
are other cases, especially in electronic products, where a "constant"
failure rate may be appropriate (although approximate). This is the
basis for MIL-STD-217 and other methods to estimate system failure
rates from consideration of the types and quantities of components
used. For many electronic components, wear-out is not a practical
failure mode. The time that the product is in use is significantly
shorter than the time it takes to reach wear-out modes. That leaves
infant mortality and normal life failure modes as the causes of all
significant failures. As we have already observed, after some time,
failures from infant mortality defects get spread out so much that they
appear to be approximately random in time. A combination of low level
infant mortality failures and some random failures caused by
operational stresses (such as power line surges) can result in a
product failure distribution that is very close to the classical normal
life period. This brings up the question of a much-misunderstood term
that applies during the normal life period, MTBF.
MTBF – What is it?
A common term used in specifying and marketing products is MTBF, which
is a vastly misunderstood (and often misused) term. MTBF historically
stands for "Mean Time Between Failures," and as such, applies only when
the underlying distribution has a constant failure rate (e.g.
an exponential distribution). In this case, MTBF is the characteristic
life parameter of the exponential distribution, as we will see below.
However, use of the term MTBF is confused by the fact that a few
reliability practitioners have used it to indicate "Mean Time Before
Failure," a case where the underlying distribution may be a wear-out
mode. Further, to some practitioners the word "between" implies a
repairable product while "before" implies a non-repairable product. To
make matters worse, vendors of many products use the term MTBF without
defining what they mean, sometimes with no concept of reliability
issues. In fact, the author has actually seen MTBF explained as
"Minimum Time Before Failure," a completely non-statistical and
nonsensical concept.
Mean
Time Before Failure (often termed Mean Time To Failure, or MTTF)
describes the average time to failure of a product, even when failure
rate is increasing over time (wear-out mode). Some units will fail
before the mean life, and some will last longer.
Thus, a product specified as having an MTTF of 50,000 hours implies
that some units will actually operate longer than 50,000 hours without
failure. Note: I'll use MTTF rather than Mean Time Before Failure for
the remainder of this article. When I write MTBF, I mean "Mean Time
Between Failures," as applies to the exponential distribution.
In
recent years, many vendors have started using terminology such as
"service life" to describe how long their products may last in use.
This is a good trend. However, while writing this article, the author
found current a data sheet that indicated "service life" using MTBF,
where the MTBF values were in excess of 500,000 hours (this would be 57
years of 24-hour-per-day operation). The products specified would not
operate, non-stop, for over 50 years; wear-out modes would kill off
most of these products in ten years, at most. The vendor was confusing
the normal life failure rate, often expressed as an MTBF value, with the wear-out distribution of the product.
How
does MTBF describe failure rate? It is quite simple: when the
exponential distribution applies (constant failure rate modeled by the
flat, bottom of the bathtub curve), MTBF is equal to the inverse of
failure rate. For example, a product with an MTBF of 3.5 million hours,
used 24 hours per day:
- MTBF = 1 / failure rate
- failure rate = 1 / MTBF = 1 / 3,500,000 hours
- failure rate = 0.000000286 failures / hour
- failure rate = 0.000286 failures / 1000 hours
- failure rate = 0.0286% / 1000 hours - and since there are 8,760 hours in a year
- failure rate = 0.25% / year
Note
that 3.5 million hours is 400 years. Do we expect that any of these
products will actually operate for 400 years? No! Long before 400 years
of use, a wear-out mode will become dominant and the population of
products will leave the normal life period of the bathtub and start up
the wear-out curve. But during the normal life period, the "constant"
failure rate will be 0.25% per year, which can also be expressed as an
MTBF of 3.5 million hours.
How does MTBF fit into the equation for the exponential distribution? MTBF is the scale parameter (usually termed eta or
h) that defines the specific model for an exponential distribution. The equation for the density
function of an exponential distribution is given by:
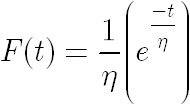
where:
- F(t) = probability of failure at time t
- h = characteristic life = MTBF (time when 63.2% cumulative failures occur)
- e = 2.71828', base of natural logs
Note that many
products with very low failure rates during "normal life" will wear out
in a few years, so that the Mean Time Before Failure (or MTTF) may be
much less than Mean Time Between Failures. Let's look at this
graphically.
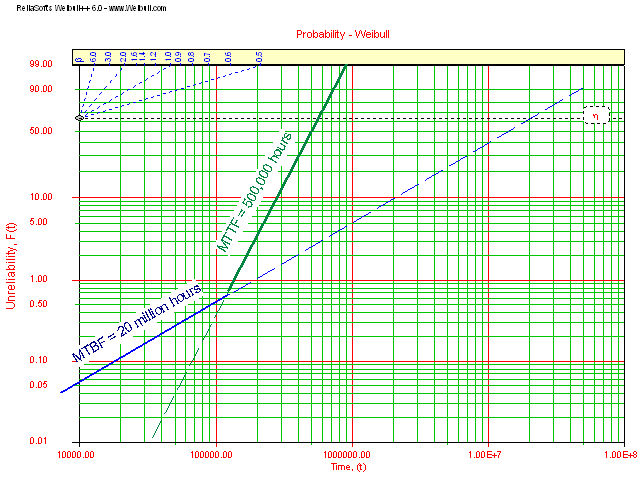
Figure 2: Weibull Plot for Normal Life and Wear-Out Populations
Figure
2 above shows a Weibull probability plot. This plot shows the expected
cumulative failures for a product over time, with time shown on the
x-axis and cumulative failure percentages (labeled Unreliability) shown
on the y-axis. This is one of the most common ways to view failure
distributions. The solid blue line is titled "MTBF = 20 million hours"
and represents the normal life period shown as a horizontal line on the
bathtub curve. It is not horizontal here because this plot shows
cumulative failures whereas the bathtub curve shows failure rate. The
MTBF of an exponential distribution is equal to the time when 63.2% of
the population of units has failed. This level is shown on the plot as
a dashed black line labeled
h (eta). In this example, the extension of the "MTBF = 20 million hours" line crosses the
63.2% level at 20 million hours on the x-axis.
The green line, on
the other hand, represents a wear-out distribution as depicted on the
right side of a bathtub curve. It is not a constant failure rate
distribution but a failure rate that increases with time. Note that it
crosses the 50% cumulative level at about 500,000 hours. This is a
wear-out distribution with an MTTF of 500,000 hours. Note that for
betas over 3, MTTF is close to the 50% cumulative failure time - Weibull++
can calculate the actual mean life (MTTF) and median life (50%
cumulative failure time) for any Weibull distribution. When beta = 1
(or an exponential distribution is used), the mean life will be the
same as Mean Time Between Failures.
Both
of these distributions (blue and green lines) apply to the same
population of devices. These devices fail primarily according to the
constant failure rate model (solid blue MTBF line) until the blue line
intercepts the green line. This is when wear-out begins to have a
significant effect (a little over 100,000 hours in this example). By
500,000 hours, half of the units will have failed and by 900,000 hours,
99% of the units will have failed. None of them will ever reach the 20
million hour MTBF time because the wear-out mode dominates after about
100,000 hours of operation. Note that the true overall cumulative
failures will be the sum of the two distributions shown on this plot.
However, because the y-axis is a log-log scale, the sum of the two
distributions is very close to the two straight lines except around the
area where they intercept.
MTBF Summary
As we have seen here, it is logical that a device can have an MTBF that
is much greater than its wear-out time because MTBF is only a
projection of the normal lifetime failures to a cumulative level of
63.2%. Most, if not all, devices will have failed due to wear-out modes
long before the MTBF time.
A major problem for many people with the term Mean Time Between Failures is that it is expressed as "time" when it is really used to indicate failure rate during the normal
life period. To further
confuse the issue, some people use the term MTBF to indicate Mean Time Before Failure, a case when it applies to wear-out modes and really does relate to service life. And, as I noted
above, some people don't know what they are talking about and claim service life is equal to "Mean Time Between Failures"!
Good
news is that recent data sheets from some vendors (particularly those
making electronic assemblies) show MTBF under the heading of
"reliability" and a separate value for service life. In this case, the
vendor has described both the expected failure rate during the normal
life period of the bathtub (e.g. "MTBF = 3.5 million hours") and the
point in time at which the product is expected to start up the wear-out part of the bathtub curve (e.g. "service life greater than 8 years"). Bad news is that some vendors,
even major technology firms, still don't understand reliability concepts, at least as expressed in their data sheets.
When
you are specifying components for a product and want to understand how
long it might operate and what the failure rate might be during normal
life, be sure to find out what the vendor means by "MTBF." And if he
thinks it means "Minimum Time Before Failure" calculated from
MIL-HDBK-217, be careful!
Everything Eventually Wears Out
In the long run, everything wears out. For many electronic designs,
wear-out will occur after a long, reasonable use-life. Inexpensive
electronic watches, radios, televisions and other such products usually
last for years, and people are not too upset if they finally fail.
There are usually newer products with better features that they want to
buy after a few years.
For
many mechanical assemblies, the wear-out time will be less than the
desired operational life of the whole product and replacement of failed
assemblies can be used to extend the operational life of the product.
With some items, wear-out is expected and replacement is a normal
routine. For example, inkjet cartridges run out of ink after so much
ink has been squirted. This is not normally thought of as a failure.
However, if a newly replaced cartridge runs out of ink after a short
period of use, then we do consider it a failure. On the other hand,
there are mechanical and electro-mechanical devices that only last for
months or years of use in a product expected to last for decades.
Relays, generators, switching devices, engine parts and hydraulic
components in aircraft are replaced on a periodic basis, usually before
they fail, to enable the aircraft to fly for many years of safe
operation. Tires and brake components are replaced several times over
the period of time that the automobile is in use.
The
wear-out period does not occur at one time for all components. The
shortest-lived component will determine the location of the wear-out
time in a given product. In designing a product, the engineer must
assure that the shortest-lived component lasts long enough to provide a
useful service life. If the component is easily replaced, such as
tires, replacement may be expected and will not degrade the perception
of the product's reliability. If the component is not easily replaced
and not expected to fail, failure will cause customer dissatisfaction.
In
order to assess wear-out time of a component, long-term testing may be
required. In some cases, a 100% duty cycle (running tires in a road
wear simulator 24 hours a day) may provide useful lifetime testing in
months. In other cases, actual product use may be 24 hours a day and
there is no way to accelerate the duty cycle. High level physical
stresses may need to be applied to shorten the test time. This is an
emerging technique of reliability assessment termed QALT (Quantitative
Accelerated Life Testing) that requires consideration of the physics
and engineering of the materials being tested.
Properly
applied, QALT can provide useful information from tests much shorter in
length than the expected operating time of a design. However, much care
must be taken to assure that all possible failure modes have been
investigated. Running a quantitative accelerated life test without
considering all possible failure modes and their accelerating stress
types may miss a significant failure mode and invalidate the
conclusions. As appropriate, mechanics, electronics, physics and
chemistry must all be considered when designing a QALT.
Note that "MTBF" testing, using many units in parallel to shorten test
times, is a popular method of life testing. It does not apply to
testing for wear-out! It can apply to testing for normal life failures,
but the results of such testing should never be extrapolated to times
longer than were used for the test itself.
Conclusion
As demonstrated in Parts One
and Two of this article, the traditional bathtub curve is a reasonable,
qualitative illustration of the key kinds of failure modes that can
affect a product. Quantitative models such as the Weibull distribution
can be used to assess actual designs and determine if observed failures
are decreasing, constant or increasing over time so that appropriate
actions can be taken. The exponential distribution and the related Mean
Time Between Failures (MTBF) metric are appropriate for analyzing data
for a product in the "normal life" period, which is characterized by a
constant failure rate. But be careful - many people have "imposed" a
constant failure rate model on products that should be characterized by
increasing or decreasing failure rates, just because the exponential
distribution is an easy model to use.
Do
not assume that a product will exhibit a constant failure rate. Use
life testing and/or field data and life distribution analysis to
determine how your product behaves over its expected lifetime. In
addition to traditional life data analysis models (such as the Weibull
distribution), quantitative accelerated life testing (QALT) may be a
valuable technique to better understand failure distributions of highly
reliable products with reduced testing time, in a cost-effective
manner. Without a QALT approach to testing, there is no way to
accurately assess the long-term reliability of a product in a short
time. If you need to understand the reliability of a device for a
one-year use-life, a non-accelerated test of 12 units for one month
will not do it. It will only provide information on one month of use.
Projection to one year will be invalid if a wear-out mode occurs, for
example, in six months. The only way to find a wear-out mode is to test
long enough to observe it, with or without a QALT approach. When
dealing with vendors and their claims of reliability for components you
wish to use, be sure you understand how they determined these figures
and how well they understand the consequences of the bathtub curve.
|
