The Bathtub Curve and Product Failure Behavior
Part One - The Bathtub Curve, Infant Mortality and Burn-in

Typical infant mortality distributions for state-of-the-art semiconductor chips follow a Weibull model with a beta in the range of 0.2 to 0.6. If such a distribution is viewed in terms of failure rate versus time, it looks like the plot in Figure 2.

Figure 2: Infant Mortality Curve - Failure Rate vs. Time

This plot shows ten years (87,600 hours) of time on the x-axis with failure rate on the y-axis. It looks a lot like the infant mortality and normal life portions of the bathtub curve in Figure 1, but this curve models only infant mortality (decreasing failure rate). Dots on this plot represent failure times typical of an infant mortality with Weibull beta = 0.2. As you can see, there are 27 failures before one year, and only 6 failures from one to ten years. People observing this curve, and the failure points plotted, could not be blamed for thinking it represents both infant mortality failures (in the first year or so), and normal life failures after that. But these are only infant mortality failures - all the way out to ten years!

This plot shows the distribution for a beta value typical of complex, high-density integrated circuits (VLSI or Very Large Scale Integrated circuits). Parts such as CPUs, interface controller and video processing chips often exhibit this kind of failure distribution over time. A look at this plot shows that if you could run these parts for the equivalent of three years and discard the failed parts, the reliability of the surviving parts would be much higher out to ten years. In fact, until a wear-out mode occurs, the reliability would continue to improve over time. If there are mechanisms that can produce normal life failures (theoretically a constant failure rate) mixed in with the defects that cause the infant mortalities shown above, burn-in can still provide significant improvement as long as the constant failure rate is relatively low. 

Burn-In for Leading Edge Technologies 
To see how burn-in can improve the reliability of high tech parts, we'll use a chart that looks somewhat like the failure rate vs time curve in Figure 2, but is more useful. This is a survival plot that directly shows how many units from a population have survived to a given time. Figure 3 is a plot for a typical VLSI process with a small "weak" sub-population (defective parts that will fail as infant mortalities) and a larger sub-population of parts that will fail randomly at a very low rate over the normal operating life. The x-axis scale is in years of use (zero to 100 years!) and the y-axis is percent of parts still operating to spec (starting at 100% and dropping to 50%).

Figure 3 shows that, of the failures that occur in the first 20 years (about 4%), most failures occur in the first year or so, just like we observed in the infant mortality example above. Because there is a low level, constant failure rate, this plot shows failures continuing for a hundred years. Of course, there could be a wear-out mode that comes into play before a hundred years has elapsed, but no wear-out distribution is considered here. Electronic components, unlike mechanical assemblies, rarely have wear-out mechanisms that are significant before many decades of operation. 

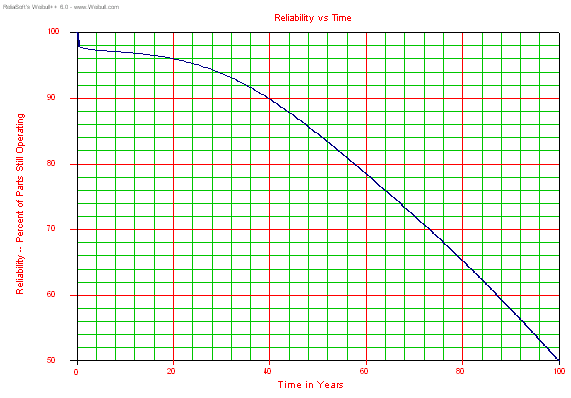Figure 3: Mixed Infant Mortality and Normal Life Survival Plot

We're not really interested in the failures much beyond ten years, so let's look at this same model for only the first ten years. In Figure 4, we have included sample failure points from the simulation model used to create the plot. These enable us to view which population (infant mortality or normal life) the failure came from.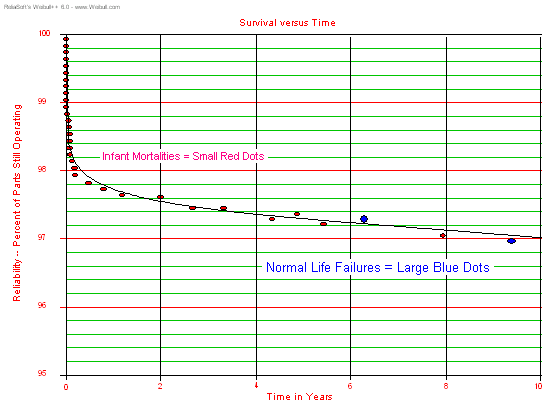

Figure 4: Mixed Infant Mortality and Normal Life Failures

We see that the plot in Figure 4 looks like the early life and normal life portions of the bathtub curve, and in fact includes both distributions. We see that over 2% of the units fail in the first year, but it takes ten years for 3% to fail. In actuality, there are still "infant" mortalities occurring well beyond ten years in this model, but at an ever-decreasing rate. In fact, in the ten year span of this model there would be very few normal life failures. Only two failures (~5% of all failures) in this example (large blue dots) come from the normal life failure population. About 95% of the failures plotted above (small red dots) are infant mortality failures! This is what the integrated circuits (IC) industry has observed with complex solid-state devices. Even after ten years of operation the primary failure cause for ICs is still infant mortality. In other words, failures are still driven primarily by defects.

In such cases, burn-in can help. In the plot above you can see that if you could get three years of operation on this part before you shipped it, you would have screened out over 80% (2½% divided by 3%) of the parts that would fail in ten years. So if we were to come up with a method to effectively "age" the parts the equivalent of three years and eliminate most of the infant mortalities, the remaining parts would be more reliable than the original population. Of course, the parts that go through the three-year "burn-in" would have to last an additional ten years in the field, for a total of thirteen years. Let's see what this looks like in Figure 5.

Figure 5: Comparison of Failures from Raw and Burned-in Parts

Above, we see fourteen years of failure distribution for the original parts (not burned-in) and eleven years of expected failure distribution for parts that received three years of burn-in. In this example, the total cumulative failures between three years and thirteen years for the original parts (or from zero to ten years for burned-in parts) is about 0.6%. Without burn-in, the first ten years would have had about 3% cumulative failures. This is about a five times reduction in cumulative failures by using burn-in, or in terms of a change, we would have about 2½% fewer cumulative failures in ten years with burn-in if a dominant infant mortality failure mode exists. Note that in the first year or two, the relative improvement in reliability is even greater. At two years, only about 0.1% failures are expected after burn-in but almost 2½% without burn-in; a ratio of almost 25:1!

In reality, manufacturers don't have two to three years to spend on burn-in. They need an accelerated stress test. In the IC industry there are usually two stresses that are used to accelerate the effective time of burn-in: temperature and voltage. Increased temperature (relative to normal operating temperatures) can provide an acceleration of tens of times (10x to 30x is typical). Increased voltages (relative to normal operating levels) can provide even higher acceleration factors on many types of ICs. Combined acceleration factors in the range of 1000:1, or more, are typical for many IC burn-in processes. Therefore, burn-in times of tens of hours can provide effective operating times of one to five years, significantly reducing the proportion of parts with infant mortality defects.

What if we try burn-in on a product with no dominant infant mortality problems? The survival plot for an assembly with a 1% per year "constant" failure rate (normal life period) is shown below in Figure 6. 

Figure 6: Survival Plot for Constant Failure Rate

It's pretty easy to see that burn-in for two years would find ~2% failures, but operation for an additional two years would find another ~2%. At ten years, we would have found about 10%. Note, the line is not really a straight line because a constant failure rate (equivalent to the normal life part of the bathtub) acts on the remaining population and the remaining population is decreasing as units fail. Looking at the same burn-in conditions as in the last example, if we were to provide three years of operation on these parts and then use them for an additional ten years, what results would we have? The cumulative failures of the units that passed this screen would be very close to 9.5%. Without burn-in, the cumulative failures in ten years would be the same, about 9.5%. There is no advantage to burn-in with a constant (normal life) failure rate.

It should be obvious that burn-in of an assembly that is failing due to a wear-out failure mode (failure rate increasing with time) will actually yield assemblies that are worse than units that did not go through burn-in. This is simply because the probability of failure is increasing for every hour the parts run. Adding operating time simply increases the possibility of a failure in any future period of time!

Conclusion
In this issue, Part One, we have introduced the concept of the bathtub curve and discussed issues related to the first period, infant mortality, as well as the practices, such as burn-in, that are used to address failures of this type. As this article demonstrates, although burn-in practices are not usually a practical economic method of reducing infant mortality failures, burn-in has proven effective for state-of-the-art semiconductors where root cause defects cannot be eliminated. For most products, stress testing, such as HALT/HAST should be used during design and early production phases to precipitate failures, followed by analysis of the resulting failures and corrective action through redesign to eliminate the root causes. In Part Two (presented in next month's HotWire), we will examine the final two periods of the bathtub curve: normal life failures and end of life wear-out.