



Next: Classification and legend for
Up: Transfer_Book
Previous: Forward Plan
Contents
Computation of parameters of T-student distribution
To compute the parameters of a T-student distribution we have to take in account the fact that some moments of the distribution might not exist, because they diverge, so we use fractional moments to avoid problems. If we consider:
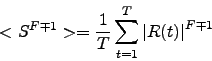 |
(A-1) |
as a fractional moment of the distribution of the returns 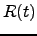 because
because 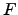 is a fractional number, and we compute the rate of the moments as:
is a fractional number, and we compute the rate of the moments as:
![\begin{displaymath}
r_{F}=\frac{<S^{F-1}>}{<S^{F+1}>}=\frac{1}{(2 k -3)\sigma^2}\left[ (k-1) \frac{2}{F}\right] - \frac{1}{(2 k -3) \sigma^2}
\end{displaymath}](img239.png) |
(A-2) |
for different exponents in the interval:
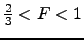 , we can see that
, we can see that
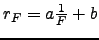 is a linear function of the parameters, so we can take the values of
is a linear function of the parameters, so we can take the values of 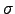 and
and 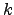 from the linear regression:
from the linear regression:
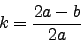 |
(A-3) |
and
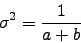 |
(A-4) |




Next: Classification and legend for
Up: Transfer_Book
Previous: Forward Plan
Contents
Ricardo Coelho
2007-05-08
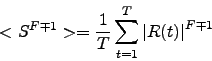
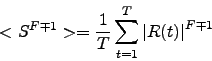
![\begin{displaymath}
r_{F}=\frac{<S^{F-1}>}{<S^{F+1}>}=\frac{1}{(2 k -3)\sigma^2}\left[ (k-1) \frac{2}{F}\right] - \frac{1}{(2 k -3) \sigma^2}
\end{displaymath}](img239.png)