From the discussion of the model in Section 
the
likelihood may be written down. Let 
be
the indexing set for all cracks, and 
be
the indexing set for observation times. The data are then
where 
is the length of crack i at time 
, and so
the likelihood is
Since the are exchangeable (that is, conditionally independent given the
and the parameters 
), the joint conditional distribution factorises as
the products of the conditional distributions, then;
and the are normally distributed with mean 
and
(in the case of constant variance,) variance 
, so the
likelihood is the product of Gaussians;
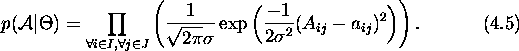
While the parameters, , do not appear explicitly in the
above expression, they are present in the , which are
deterministic functions of the crack parameters.
