Course 442 - General Relativity
Lecturer: P.S. Florides
Date: 1996-97
Groups: Optional JS and SS Theoretical Physics, JS and SS Mathematics
Prerequisites:
211, 221, 241
Duration: 21 weeks.
Lectures per week: 3
Assessment:
Examinations: One 3-hour examination
Mathematical Background
Linear and Multilinear algebra, general tensors, tensor
products, tests for tensor character, inner product, associated
tensors (overview). Differentiable manifolds
(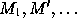 ),
differentiable functions, differentiable mappings
),
differentiable functions, differentiable mappings
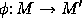 ,
tangent vectors, tangent spaces and their duals (briefly).
,
tangent vectors, tangent spaces and their duals (briefly).
The differential (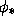 ) of a map
) of a map
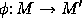 and its dual (
and its dual (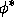 ).
Vector fields and their commutator product,
1-form fields, tensor fields, moving frames. Differentiable
curves, and vector fields on such curves, integral curves,
r-surfaces.
).
Vector fields and their commutator product,
1-form fields, tensor fields, moving frames. Differentiable
curves, and vector fields on such curves, integral curves,
r-surfaces.
Affine manifolds, connection coefficients, covariant derivatives
of vector, 1-form and tensor fields, parallel propagation along
a differentiable curve, intrinsic derivatives , Geodesics. The
Riemann tensor and the torsion tensor.
Riemannian manifolds, the Riemann connection, properties of the
Riemann tensor; the Ricci and Einstein tensors. The necessary
and sufficient condition for a Riemannian manifold to be
flat.
Equation of geodesic deviation, stationary properties of geodesics,
Riemannian curvature, spaces of constant curvature, Schurs theorem.
General Relativity (G.R.)
Physical foundations of G.R., space-time as a Riemannian
manifold, Einstein's field equations. The linearized Einstein
field equations, Newton's theory as a first approximation, further
(exact) analogies between Newton's and Einstein's theories.
(Digression: Lie derivatives, groups of motions, killing vectors.
General form of the metric with spherical symmetry).
Exact solutions of Einstein's equations. The Schwarzschild
exterior solution, Birkhoff's theorem, the three ``crucial tests'',
the generalized red-shift formula. Study of the Schwarzschild
radius, the Eddington - Finkelstein coordinates, Kruskal
coordinates, black holes.
Dynamics of perfect fluids, the Oppenheimer-Volkov equation,
maximum mass, the interior Schwarzschild solution; the Einstein
and de Sitter Universes.
Electromagnetic Theory
The electromagnetic tensor, the electromagnetic energy tensor,
the combined Einstein-Maxwell field equations, motion of
charged particles in a electromagnetic field (in curved space-time),
the Reissner-Nordström solution.
[Selected topics (time permitting): variational principles
and conservation laws, (linearized) gravitational radiation,
standard cosmology].
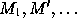 ),
differentiable functions, differentiable mappings
),
differentiable functions, differentiable mappings
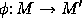 ,
tangent vectors, tangent spaces and their duals (briefly).
,
tangent vectors, tangent spaces and their duals (briefly).
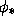 ) of a map
) of a map
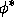 ).
Vector fields and their commutator product,
1-form fields, tensor fields, moving frames. Differentiable
curves, and vector fields on such curves, integral curves,
r-surfaces.
).
Vector fields and their commutator product,
1-form fields, tensor fields, moving frames. Differentiable
curves, and vector fields on such curves, integral curves,
r-surfaces.