Lecturer: Dr. T.G. Murphy
Date: 1997-98
Groups: Optional JS and SS Mathematics, SS Two-subject Moderatorship
Duration: 21 weeks
Lectures per week: 3
Examinations: Probably examined in 3 parts, one examination covering each term's work
The principal aim of the course is to prove the Prime Number Theorem, which states that the nth prime pn is of order n log n. This result was proved using a revolutionary method introduced by Riemann in 1858, which made use of the then newly-minted theory of complex functions. Riemann showed that many problems concerning the distribution of primes could be expressed in terms of his zeta function
He did not succeed in proving the Prime Number Theorem himself; he could only show that it followed from the so-called Riemann Hypothesis. This Hypothesis states that the zeros of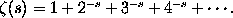
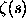 all lie on the line Im(s) = 1/2.
The Prime Number Theorem (which had been postulated by Gauss)
was finally proved just 100 years ago
by Hadamard and de la Vallée Poussin (independently)
using Riemann's method,
after showing that the zeros of
all lie on the line Im(s) = 1/2.
The Prime Number Theorem (which had been postulated by Gauss)
was finally proved just 100 years ago
by Hadamard and de la Vallée Poussin (independently)
using Riemann's method,
after showing that the zeros of 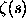 cannot lie too far off the `critical line'.
The Riemann Hypothesis has still not been proved (or disproved);
after Wiles' proof of Fermat's Last Theorem
(which incidentally made considerable use of zeta functions),
it remains the greatest unsolved problem in mathematics.
At the same time,
zeta functions have proved a tool of enormous importance
not just in number theory
but throughout pure and applied mathematics.
For example, the zeta function of an operator E
with eigenvalues
cannot lie too far off the `critical line'.
The Riemann Hypothesis has still not been proved (or disproved);
after Wiles' proof of Fermat's Last Theorem
(which incidentally made considerable use of zeta functions),
it remains the greatest unsolved problem in mathematics.
At the same time,
zeta functions have proved a tool of enormous importance
not just in number theory
but throughout pure and applied mathematics.
For example, the zeta function of an operator E
with eigenvalues
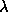 1,
1,
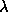 2,...
defined by
2,...
defined by
turns out to encode exactly those properties of E required in certain aspects of quantum field theory. The course is in 3 parts:
Definitions of a prime.
Euclid's theorem (that there are an infinity of primes).
The Fundamental Theorem of Arithmetic (Unique Factorisation Theorem).
The sieve of Eratosthenes.
Euler's Product Formula.
Euler's Theorem ( 1/p diverges).
1/p diverges).
Riemann's zeta function.
The function  (x).
(x).
Statement of the Prime Number Theorem.
Computer tests for primality.
Fermat's Little Theorem.
Carmichael numbers.
The elliptic curve method.
Valuations.
P-adic numbers.
Function fields and their primes.
Number fields and their primes.
Complex function theory (review)
Analytic extension of 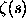 .
.
The Mellin transform.
The functional equation of 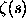 .
.
The Riemann hypothesis.
Proof of the Prime Number Theorem.
Primes in arithmetic sequence (Dirichlet's Theorem)
The Prime Number Theorem in number fields.