-
The finite fields
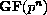 their existence and uniqueness.
their existence and uniqueness.
- Object-oriented programming and finite fields
The second part of the course, given by Dr Purser, will cover:
- Introduction to codes, Hamming distance, etc.
- Linear block codes, parity check matrices, Hamming codes.
- Ideals and binary cyclic codes.
- Finite fields and BCH codes.
- Error-correcting techniques.
- Some examples: CCITT, BSC, Ethernet, EBU.
- Non-binary codes. Reed-Solomon codes.
- Convolutional Codes.
- Decoding of convolutional codes (Viterbi algorithm).
- Theoretical foundations of coding theory: Information Theory.
- Modelling channels, capacity and Shannon's theorem.
- Bounds and limits.