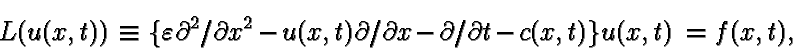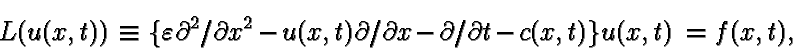Discrete Approximation of the Riemann Problem for the Viscous Burgers Equation

Discrete Approximation of the Riemann Problem for the Viscous Burgers Equation

In this paper we consider discrete approximations of a Dirichlet problem for the quasilinear parabolic equation

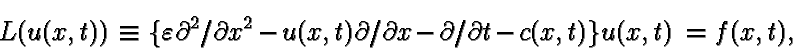
$L(u(x,t))\equiv\{\varepsilon \partial ^2/\partial x^2-u(x,t)\partial/ \partial x -\partial /\partial t-c(x,t)\}u(x,t)=f(x,t),$

that is, the viscous Burgers equation. The singular perturbation parameter e takes arbitrary values from the half-interval (0,1]. The initial condition has a discontinuity of the first kind at the point S^*=(0,0) such that j₀(+0)-j₀(-0)>0, where u(x,0)=j₀(x); thus, we have the Riemann problem. For such a problem we construct special finite difference schemes controlled by the parameter e and by the type of the singularities, which the solution u(x,t) exhibits. The discrete solution for this problem is shown to converge uniformly with respect to the parameter e in a uniform grid metric.