In this paper we consider mesh approximations of a boundary
value problem for singularly perturbed elliptic equations of
convection-diffusion type on a strip. To approximate the
equations, we use classical finite difference approximations on
piecewise-uniform meshes condensing in a neighbourhood of
the boundary layer. The approximation errors of
solutions and derivatives are analysed in the
r-metric.
In this metric the error of a solution is defined by an
absolute error, while the error of its derivative
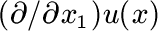 ,
i.e. the derivative in the direction across
of the boundary layer, is defined by the relative error in that part
of the domain where the derivative is large, and by the absolute
error in the remainder part of the domain. It is shown that in
the class of meshes, whose stepsize in the boundary layer does not
decrease with moving away from the outflow boundary, there are no
meshes on which the scheme converges
e-uniformly in the
r-metric. We establish conditions,
imposed on the distribution
of the nodes of piecewise uniform meshes, under which the scheme
converges in the r-metric
e-uniformly up to a
logarithmic factor.
,
i.e. the derivative in the direction across
of the boundary layer, is defined by the relative error in that part
of the domain where the derivative is large, and by the absolute
error in the remainder part of the domain. It is shown that in
the class of meshes, whose stepsize in the boundary layer does not
decrease with moving away from the outflow boundary, there are no
meshes on which the scheme converges
e-uniformly in the
r-metric. We establish conditions,
imposed on the distribution
of the nodes of piecewise uniform meshes, under which the scheme
converges in the r-metric
e-uniformly up to a
logarithmic factor.