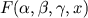 darstellbaren Functionen.
darstellbaren Functionen.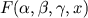 darstellbaren Functionen.
darstellbaren Functionen.
Am 6. November 1856 wurde der königlichen Societät eine
von ihrem Assessor, Herrn Doctor Riemann, eingereichte
mathematische Abhandlung vorgelegt, welche
,,Beiträge zur Theorie der durch die Gauss'sche Reihe
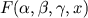 darstellbaren Functionen}`` enthält.
darstellbaren Functionen}`` enthält.
Diese Abhandlung ist einer Classe von Functionen gewidmet, welche
bei der Lösung mancher Aufgaben der mathematischen Physik
gebraucht werden. Aus ihnen gebildete Reihen leisten bei
schwierigeren Problemen dieselben Dienste, wie in den einfacheren
Fällen die jetzt so vielfach angewandten Reihen, welche nach
Cosinus und Sinus der Vielfachen einer veränderlichen
Grösse fortschreiten. Diese Anwendungen, namentlich
astronomische, scheinen, nachdem schon Euler sich aus
theoretichem Interesse mehrfach mit diesen Functionen
beschäftigt hatte, Gauss zu seinen Untersuchungen über
dieselben veranlasst zu haben, von denen er einen Theil in seiner
der Kön. Soc. im J. 1812 übergebenen Abhandlung
über die Reihe, welche er durch
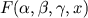 bezeichnet, veröffentlicht hat.
bezeichnet, veröffentlicht hat.
Diese Reihe ist eine Reihe, in welcher der Quotient des (n + 1)ten Gliedes in das folgende
und das erste Glied = 1 ist. Die für sie jetzt gewöhnliche Benennung hypergeometrische Reihe ist schon früher von Johann Friedrich Pfaff für die allgemeineren Reihen vorgeschlagen worden, in denen der Quotient eines Gleides in das folgende eine rationale Function des Stellenzeigers ist; während Euler nach Wallis darunter eine Reihe verstand, in welcher dieser Quotient eine ganze Function ersten Grades des Stellenzeigers ist.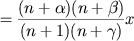
Die unveröffentlichte Theil der Gauss'schen Untersuchungen über diese Reihe, welcher sich in seinem Nachlasse vorgefunden hat, ist unterdessen schon im J. 1835 durch die im 15. Bande des Journals von Crelle enthaltenen Arbeiten Kummer's ergänzt worden. Sie betreffen die Ausdrücke der Reihe durch ähnliche Reihen, in denen statt des Elements x eine algebraische Function dieser Grösse vorkommt. Einen speciellen Fall dieser Umformungen hatte schon Euler aufgefunden und in seiner Integralrechnung, so wie in mehren Abhandlungen behandelt (in der einfachsten Gestalt in den N. Acta Acad. Petr. T. XII. p. 58); und diese Relation ward später von Pfaff (Disquis. anal. Helmstadii 1797), Guderman (Crelle J. Bd. 7. S. 306) und Jacobi auf verschiedenen Wegen bewiesen. Kummer gelang es, die Methode Euler's zu einem Verfahren auszubilden, durch welches sämmtliche Transformationen gefunden werden konnten; die wirkliche Ausführung desselben erforderte aber so weitläufige Discussionen, dass er für die Transformationen dritten Grades von der Durchführung derselben abstand und sich begnügte, die Transformationen ersten und zweiten Grades und die aus ihnen zusammengesetzten vollständig abzuleiten.
In der anzuzeigenden Abhandlung wird auf diese Transcendenten eine Methode angewandt, deren Princip in der Inaug. Diss. des Verfassers (Art. 20) ausgesprochen worden ist und durch die sich sämmtliche früher gefundenen Resultate fast ohne Rechnung ergeben. Einige weitere mittelst derselben Methode gewonnenen Ergebnisse hofft der Verf. demnächst der Königlichen Societät vorlegen zu können.