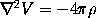 ,
for Laplace's form of it,
,
for Laplace's form of it,
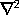 V
= 0, was first published in 1813. Lastly, I may mention his memoir in
1825 on the theory of waves.
V
= 0, was first published in 1813. Lastly, I may mention his memoir in
1825 on the theory of waves.
From `A Short Account of the History of Mathematics' (4th edition, 1908) by W. W. Rouse Ball.
Siméon Denis Poisson, born at Pithviers on June 21, 1781, and died at Paris on April 25, 1840, is almost equally distinguished for his applications of mathematics to mechanics and to physics. His father had been a private soldier, and on his retirement was given some small administrative post in his native village; when the revolution broke out he appears to have assumed the government of the place, and, being left undisturbed, became a person of some local importance. The boy was put out to nurse, and he used to tell how one day his father, coming to see him, found that the nurse had gone out, on pleasure bent, having left him suspended by a small cord attached to a nail fixed in the wall. This, she explained, was a necessary precaution to prevent him from perishing under the teeth of the various animals and animalculae that roamed the floor. Poisson used to add that his gymnastic efforts carried him incessantly from one side to the other, and it was thus in his tenderest infancy that he commenced those studies on the pendulum that were to occupy so large a part of his mature age.
He was educated by his father, and destined much against his will to be a doctor. His uncle offered to teach him the art, and began by making him prick the veins of cabbage-leaves with a lancet. Wen perfect in this, he was allowed to put on blisters; but in almost the first case he did this by himself, the patient died in a few hours, and although all the medical practitioners of the place assured him that ``the event was a very common one,'' he vowed he would have nothing more to do with the profession.
Poisson, on his return home after this adventure, discovered amongst the official papers sent to his father a copy of the questions set at the Polytechnic school, and at once found his career. At the age of seventeen he entered the Polytechic, and his abilities excited the interest of Lagrange and Laplace, whose friendship he retained to the end of their lives. A memoir on finite differences which he wrote when only eighteen was reported on so favourably by Legendre that it was ordered to be published in the Recueil des savants étrangers. As soon as he had finished his course he was made a lecturer at the school, and he continued through his life to hold various government scientific posts and professorships. He was somewhat of a socialist, and remained a rigid republican till 1815, when, with a view to making another empire impossible, he joined the legitimists. He took, however, no active part in politics, and made the study of mathematics his amusement as well as his business.
His works and memoirs are between three and four hundred in number. The chief threatises which he wrote were his Traité de mécanique, published in two volumes, 1811 and 1833, which was long a standard work; his Théorie mathématique de la chaleur, 1835, to which a supplement was added in 1837; and his Recherches sur la probabilité des jugements, 1837. He had intended, if he had lived, to write a work which should cover all mathematical physics and in which the results of the three books last named would have been incorporated.
Of his memoirs in pure mathematics the most important are those on definite integrals, and Fourier's series, their application to physical problems constituting one of his chief claims to distinction; his essays on the calculus of variations; and his papers on the probability of the mean results of observations.
Perhaps the most remarkable of his memoirs in applied mathematics are
those on the theory of electrostatics and magnetism, which originated
a new branch of mathematical physics; he suppose that the results were
due to the attractions and repulsions of imponderable particles. The
most important of those on physical astronomy are the two read in 1806
(printed in 1809) on the secular inequalities of the mean motions of
the planets, and on the variation of arbitrary constants introduced
into the solutions of questions on mechanics; in these Poisson
discusses the question of the stability of the planetary orbits (which
Lagrange had already proved to the first degree of approximation for
the disturbing forces), and shews that the result can be extended to
the third order of small quantities: these were the memoirs which led
to Lagrange's famous memoir of 1808. Poisson also published a paper
in 1821 on the libration of the moon; and another in 1827 on the
motion of the earth about its centre of gravity. His most important
memoirs on the theory of attraction are one in 1829 on the attraction
of spheroids, and another in 1835 on the attraction of a homogeneous
ellipsoid: the substitution of the correct equation involving the
potential, namely,
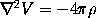 ,
for Laplace's form of it,
,
for Laplace's form of it,
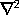 V
= 0, was first published in 1813. Lastly, I may mention his memoir in
1825 on the theory of waves.
V
= 0, was first published in 1813. Lastly, I may mention his memoir in
1825 on the theory of waves.
This page is included in a collection of mathematical biographies taken from A Short Account of the History of Mathematics by W. W. Rouse Ball (4th Edition, 1908).
Transcribed by