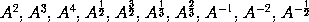
Sir Isaac Newton,
The Mathematical Principles of Natural Philosophy
(Philosophiae Naturalis Principia Mathematica)
Book Two.
Translated by Andrew Motte (1729).
The moment of any Genitum is equal to the moments of each of the generating sides drawn into the indices of the powers of those sides, and into their coefficients continually.
I call any quantity a Genitum, which is not made by addition or subduction of divers parts, but is generated or produced in arithmetic by the multiplication, division, or extraction of the root of any terms whatsoever; in geometry by the invention of contents and sides, or of the extreams and means of proportionals. Quantities of this kind are products, quotients, roots, rectangles, squares, cubes, square and cubic sides and the like. These quantities I here consider as variable and indetermined, and increasing or decreasing as it were by a perpetual motion or flux; and I understand their momentaneous increments or decrements by the name of Moments; so that the increments may be esteem'd as added, or affirmative moments; and the decrements as subducted, or negative ones. But take care not to look upon finite particles as such. Finite particles are not moments, but the very quantities generated by the moments. We are to conceive them as the just nascent principles of finite magnitudes. Nor do we in this Lemma regard the magnitude of the moments, but their first proportion as nascent. It will be the same thing, if, instead of moments, we use either the Velocities of the increments and decrements (which may also be called the motions, mutations, and fluxions of quantities) or any finite quantities proportional to those velocities. The coefficient of any generating side is the quantity which arises by applying the Genitum to that side.
Wherefore the sense of the Lemma is, that if the moments of any quantities A, B, C, &c. increasing or decreasing by a perpetual flux, or the velocities of the mutations which are proportional to them, be called a, b, c, &c. the moment or mutation of the generated rectangle AB will be aB + bA; the moment of the generated content ABC will be aBC + bAC + cAB: and the moments of the generated powers
will be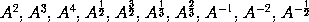
respectively. And in general, that the moment of any power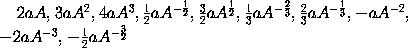
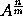 will be
will be
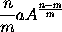 Also that the moment of the generated quantity
A²B
will be
2aAB + bA²;
the moment of the generated quantity
Also that the moment of the generated quantity
A²B
will be
2aAB + bA²;
the moment of the generated quantity
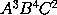 will be
will be
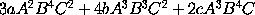 ;
and the moment of the generated quantity
;
and the moment of the generated quantity
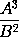 or
or
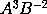 will be
will be
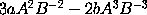 ;
and so on. The Lemma is thus demonstrated.
;
and so on. The Lemma is thus demonstrated.
Case 1.
Any rectangle as AB augmented by a perpetual flux, when, as yet,
there wanted of the sides A and B half their moments
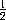 a
and
a
and
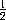 b,
was
A -
b,
was
A -
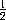 a
into
B -
a
into
B -
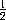 b,
or
AB -
b,
or
AB -
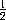 aB
-
aB
-
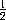 Ba
+
Ba
+
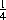 ab;
but as soon as the sides A and B are augmented by the other half
moments; the rectangle becomes
A +
ab;
but as soon as the sides A and B are augmented by the other half
moments; the rectangle becomes
A +
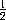 a
into
B +
a
into
B +
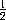 b,
or
AB +
b,
or
AB +
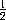 aB
+
aB
+
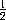 Ba
+
Ba
+
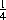 ab.
From this rectangle subduct the former rectangle, and there will
remain the excess aB + bA.
Therefore with the whole increments a
and b of the sides, the increment aB + bA of the
rectangle is generated.
Q.E.D.
ab.
From this rectangle subduct the former rectangle, and there will
remain the excess aB + bA.
Therefore with the whole increments a
and b of the sides, the increment aB + bA of the
rectangle is generated.
Q.E.D.
Case 2. Suppose AB always equal to G, and then the moment of the content ABC or GC (by Case 1.) will be gC + cG, that is, (putting AB and aB + bA for G and g) aBC + bAC + cAB. And the reasoning is the same for contents, under never so many sides. Q.E.D.
Case 3.
Suppose the sides A, B, and C, to be always equal among
themselves; and the moment aB + bA, of
A²,
that is, of the
rectangle AB, will be 2aA; and the moment
aBC + bAC + cAB of
A³,
that is, of the content ABC, will be
3aA².
And by the same reasoning the moment of any power
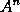 is
is
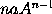 .
Q.E.D.
.
Q.E.D.
Case 4.
Therefore since
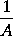 into A is 1, the
moment of
into A is 1, the
moment of
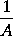 drawn into A, together with
drawn into A, together with
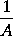 drawn into a, will be the moment of 1,
that is, nothing. Therefore the moment of
drawn into a, will be the moment of 1,
that is, nothing. Therefore the moment of
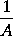 or of
or of
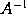 is
is
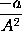 .
And generally, since
.
And generally, since
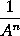 into
into
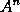 is 1, the moment of
is 1, the moment of
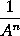 drawn into
drawn into
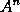 together with
together with
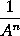 into
into
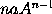 will be nothing. And
therefore the moment of
will be nothing. And
therefore the moment of
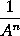 or
or
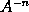 will be
will be
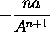 .
Q.E.D.
.
Q.E.D.
Case 5.
And since
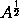 into
into
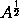 is A, the moment of
is A, the moment of
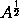 drawn into
2
drawn into
2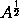 will be a, (by Case 3:) and therefore the moment of
will be a, (by Case 3:) and therefore the moment of
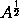 will be
will be
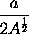 or
or
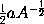 .
And generally putting
.
And generally putting
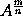 equal to B, then
equal to B, then
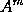 will be equal to
will be equal to
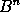 ,
and therefore
,
and therefore
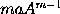 equal to
equal to
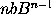 ,
and
,
and
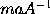 equal to
equal to
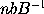 or
or
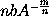 ;
and therefore
;
and therefore
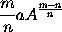 is equal to b, that is, equal to the moment of
is equal to b, that is, equal to the moment of
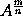 .
Q.E.D.
.
Q.E.D.
Case 6.
Therefore the moment of any generated quantity
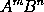 is the moment of
is the moment of
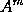 drawn into
drawn into
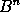 ,
together with the moment of
,
together with the moment of
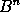 drawn into
drawn into
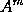 ,
that is,
,
that is,
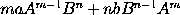 ;
and that whether
the indices m and n of the powers be whole numbers or fractions,
affirmative or negative. And the reasoning is the same for contents
under more powers.
Q.E.D.
;
and that whether
the indices m and n of the powers be whole numbers or fractions,
affirmative or negative. And the reasoning is the same for contents
under more powers.
Q.E.D.
Cor. 1 Hence in quantities continually proportional, if one term is given, the moments of the rest of the terms will be as the same terms multiplied by the number of intervals between them and the given term. Let A, B, C, D, E, F, be continually proportional; then if the term C is given, the moments of the rest of the terms will be among themselves, as -2A, -B, D, 2E, 3F.
Cor. 2 And if in four proportionals the two means are given, the moments of the extremes will be as those extremes. The same is to be understood of the sides of any given rectangle.
Cor. 3. And if the sum or difference of two squares is given, the moments of the sides will be reciprocally as the sides.
In a letter of mine to Mr. J. Collins, dated December 10. 1672 having described a method of Tangents, which I suspected to be the same with Slusius's method, which at that time was not made publick; I subjoined these words; This is one particular, or rather a corollary, of a general method, which extends itself, without any troublesome calculation, not only to the drawing of Tangents to any Curve lines, whether Geometrical or Mechanical, or any how respecting right lines or other Curves, but also to the resolving other abstruser kinds of Problems about the crookedness, areas, lengths, centres of gravity of Curves, &c. nor is it (as Hudden's method de Maximis & Minimis) limited to equations which are free from surd quantities. This method I have interwoved with that other of working in equations, by reducing them to infinite series. So far that letter. And these last words relate to a Treatise I composed on that subject in the year 1671. The foundation of the general method is contained in the preceding Lemma.
Links:
D.R. Wilkins