ROYAL IRISH ACADEMY, May 22nd, 1837
SIR WILLIAM HAMILTON laid before the Academy an account of some investigations in which he had recently been engaged, respecting Equations of the Fifth Degree. They related chiefly to three points: first the argument of Abel against the possibility of generally and algebraically resolving such equations; second, the researches of Mr. Jerrard; and third, the conceivable reduction, in a new way, of the original problem to a more simple form.
1. The argument of Abel consisted of two principal parts; one independent of the degree of the equation, and the other dependent on that degree. The general principle was first laid down, by him, that whatever may be the degree n of any general algebraic equation, if it be possible to express a root of that equation, in terms of the coefficients, by any finite combination of rational functions, and of radicals with prime exponents, then every radical in such an expression, when reduced to its most simple form, must be equal to a rational (though not a symmetric) function of the n roots of the original equation; and must, when considered as such a function, have exactly as many values, arising from the permutations of those n roots among themselves, as it has values, when considered as a radical, arising from the introduction of factors which are roots of unity. And in proceeding to apply this general principle to equations of the fifth degree, the same illustrious mathematician employed certain properties of functions of five variables, which may be condensed into the two following theorems: that, if a rational function of five independent variables have a prime power symmetric, without being symmetric itself, it must be the square root of the product of the ten squares of differences of the five variables, or at least that square root multiplied by some symmetric function; and that, if a rational function of the same variables have, itself, more than two values, its square, its cube, and its fifth power have, each, more than two values also. Sir W. H. conceived that the reflections into which he had been led, were adapted to remove some obscurities and doubts which might remain upon the mind of a reader of Abel's argument; he hoped also that he had thrown light upon this argument in a new way, by employing its premisses to deduce, à priori, the known solutions of quadratic, cubic, and biquadratic equations, and to show that no new solutions of such equations, with radicals essentially different from those at present used, remain to be discovered: but whether or no he had himself been useful in this way, he considered Abel's result as established: namely, that it is impossible to express a root of the general equation of the fifth degree, in terms of the coefficients of that equation, by any finite combination of radicals and rational functions.
2. What appeared to him the fallacy in Mr. Jerrard's very ingenious attempt to accomplish this impossible object, had been already laid before the British Association at Bristol, and was to appear in the forthcoming volume of the reports of that Association. Meanwhile Sir William Hamilton was anxious to state to the Academy his full conviction, founded both on theoretical reasoning and on actual experiment, that Mr. Jerrard's method was adequate to achieve an almost equally curious and unexpected transformation, namely, the reduction of the general equation of the fifth degree, with five coefficients, real or imaginary, to a trinomial form; and therefore ultimately to that very simple state, in which the sum of an unknown number, (real or imaginary), and of its own fifth power, is equalled to a known (real or imaginary) number. In this manner, the general dependence of the modulus and amplitude of a root of the general equation of the fifth degree, on the five moduli and five amplitudes of the five coefficients of that equation, is reduced to the dependence of the modulus and amplitude of a new (real or imaginary) number on the one modulus and one amplitude of the sum of that number and its own fifth power; a reduction which Sir William Hamilton regards as very remarkable in theory, and as not unimportant in practice, since it reduces the solution of any proposed numerical equation of the fifth degree, even without imaginary coefficients, to the employment, without tentation, of the known logarithmic tables, and of two new tables of double entry, which he has had the curiosity to construct and to apply.
3. It appears possible enough, that this transformation, deduced from Mr. Jerrard's principles, conducts to the simplest of all forms under which the general equation of the fifth degree can be put; yet, Sir William Hamilton thinks, that algebraists ought not absolutely to despair of discovering some new transformation, which shall conduct to a method of solution more analogous to the known ways of resolving equations of lower degrees, though not, like them, dependent entirely upon radicals. He inquires in what sense it is true, that the general equation of the fifth degree would be resolved, if, contrary to the theory of Abel, it were possible to discover, as Mr. Jerrard and others have sought to do, a reduction of that general equation to the binomial form, or to the extraction of a fifth root of an expression in general imaginary? And he conceives, that the propriety of considering such extraction as an admitted instrument of calculation in elementary algebra, is ultimately founded on this: that the two real equations
into which the imaginary equation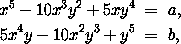
resolves itself, may be transformed into two others which are of the forms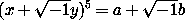
so that each of these two new equations expresses one given real number as a known rational function of one sought real number. But notwithstanding the interest which attaches to these two particular forms of rational functions, and generally to the analogous forms which present themselves in separating the real and imaginary parts of a radical of the nth degree; Sir William Hamilton does not conceive that they both possess so eminent a prerogative of simplicity as to entitle the inverses of them alone to be admitted among the instruments of elementary algebra, to the exclusion of the inverses of all other real and rational functions of single real variables. And he thinks, that since Mr. Jerrard has succeeded in reducing the general equation of the fifth degree, with five imaginary coefficients, to the trinomial form above described, which resolves itself into the two real equations following,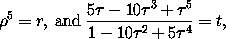
it ought now to be the object of those who interest themselves in the improvement of this part of algebra, to inquire, whether the dependence of the two real numbers x and y, in these two last equations, on the two real numbers a and b, cannot be expressed by the help of the real inverses of some new real and rational or even transcendental functions of single real variables; or, (to express the same thing in a practical, or in a geometrical form,) to inquire whether the two sought real numbers cannot be calculated by a finite number of tables of single entry, or constructed by the help of a finite number of curves: although the argument of Abel excludes all hope that this can be accomplished, if we confine ourselves to those particular forms of rational functions which are connected with the extraction of radicals.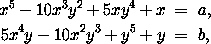
Links:
D.R. Wilkins