OUR PORTRAIT GALLERY. - NO. XXVI.
SIR WILLIAM R. HAMILTON,
Professor of Astronomy in the University of Dublin,
Astronomer Royal for Ireland,
President of the Royal Irish Academy, &c. &c.
[Robert Perceval Graves]
[Dublin University Magazine, vol. 19 (1842), pp. 94-110.]
The name of an English Sir William Hamilton, the ambassador at the
court of Naples, is still unforgotten as holding a distinguished place
among the virtuosos of his time; and Scotland boasts at present of
another Sir William Hamilton, who fills the chair of logic in her
metropolitan university, and whose reputation as a champion of his
national school of logic and metaphysics is eminent throughout Europe;
we Irishmen have also our Sir William Hamilton - SIR WILLIAM
ROWAN HAMILTON: with peculiar gratification we this month suspend his
portrait in our gallery; and, as we do so, we risk nothing in
predicting, that to him, his achievements of science, and his fame,
Ireland will in years far distant jealously vindicate her title, as
among the intellectual possessions of which she has most reason to be
proud.
Sir William Hamilton, we are happy to think, is still a young man,
being now in the thirty-seventh year of his age. He was born on the
4th of August 1805, in the house of his father, Mr. Archibald
Hamilton, in Dominick-street, Dublin. His father was by profession a
solicitor, and is still remembered by many in this city as a gentleman
possessing character and abilities which gave him a high place in
general estimation. The branch to which he belongs of the respectable
family of Hamilton, settled, we are informed, in the north of Ireland,
in the reign of James the First; its leading representative being
subsequently a baronet of some local distinction, Sir James Hamilton,
to whose title, it has been thought by members of the family, that
the legitimate succession was vested in the uncle of the subject of
our memoir, although investigations, at one time entered upon with a
view to substantiating the claim, were rendered fruitless by a defect
in some country parish register.
At the very earliest age indications were perceived of W. R. H.'s
possession of extraordinary intellectual powers, in consequence of
which, his father, unable from professional occupation to superintend
their development himself, and recognising with a laudable promptitude
their extent and value, consigned him when less than three years old
to the care of the Rev. James Hamilton, the uncle of the young
genius. To this affectionate relative and estimable man, who was
then, and is still, curate of Trim, in the county of Meath, and whose
own collegiate course had been distinguished both in science and
classics,1
belongs to the honour of being the chief, we believe we might almost
say, the sole early instructor of his nephew, whose home continued to
be with him at Trim until he became an undergraduate at the
university.
In consequence of Mr. A. Hamilton, the father, having some friends
among the body who then held the patronage of India, he originally
destined his son to a life in the east, and accordingly directed that
the mind of the child should be early employed in the acquisition of
the oriental languages. Happily the subsequent development of his
scientific powers frustrated this plan, but its immediate results were
too remarkable in themselves, and for the proof they give of the
activity and versatility of his faculties, to allow us to pass them
unnoticed. At the age of four he had made some progress in Hebrew: in
the two succeeding years he had acquired the elements of Greek and
Latin; and when thirteen years old was in different degrees acquainted
with thirteen languages, besides the vernacular - Syriac, Persian,
Arabic, Sanscrit, Hindoostanee, Malay, French, Italian, Spanish and
German; and we are not sure that this list is a complete one. We well
remember to have heard, long before we ever saw our friend, of
Dr. Meredith, formerly fellow of Trinity College, and a man of great
learning and ability, reporting with expressions of astonishment, that
he had examined in the country a child of six or seven, who read and
translated and understood Hebrew better than many candidates for
fellowship; this child was young Hamilton: we know also that he not
unfrequently wrote letters in Persian; and we think the anecdote
should not be lost, that one which he sent in that language as a
greeting to the Persian Ambassador, Mirza Abou Hassan Khan, when on a
visit to Dublin in 1819, drew from the ambassador the exclamation,
that he did not think there was a man in these countries who could
have indited such a letter. We believe Sir William has not found it
possible or thought it worth his while to keep up his knowledge of all
the languages which we have mentioned as occupying his attention in
childhood, and that he scarcely ever makes an allusion to these early
acquisitions: they constitute, however, an essential part of his
intellectual history, and as such claim a record even in the present
sketch. It is pleasant to be able to add, and, considering the
advancement made by him in both departments, the fact is wonderful,
that early as he was trained to the acquirement of languages and the
pursuit of science, this training does not appear to have been a mere
hotbed-forcing of the intellect, but to have allowed free play and
proportionate encouragement to the physical, and imaginative, and
moral energies of the human being. We believe that there was not, in
his childhood, the want of any element natural and appropriate to that
stage of his existence, and that he was then equally a boy, as he is
now, in the fullest sense of the word, a man.
We now turn from this record of the literary pursuits of his youth to
trace cursorily the history of his scientific powers and
investigations,- that department of his history, which, as more
identified with his public character, will, perhaps, excite a peculiar
interest. For the whole of what, for want of a proper word, we have
called, by way of distinction, his literary education, he owns
himself indebted, we know, to his uncle: in science he was more
self-taught. At the age of ten, having accidently fallen-in with a
Latin copy of Euclid, he became rapidly and deeply immersed in the
study of geometry; and a little before this he had acquired a liking
for arithmetical calculation, and was beginning to take an interest in
the elements of algebra, a taste which had become fully confirmed when
he had reached the age of twelve. In testimony of this we may
introduce the anecdote that it was at this time that Zerah Colburn,
the American boy was exhibited in Dublin, as an arithmetical prodigy,
and that opportunities occurred for trials of skill between him and
Hamilton, in which, rather in play than otherwise, they exchanged
questions and fought arithmetical duels; but we have heard Sir William
declare, that in these encounters his competitor was usually the more
expert of the two combatants. Between the ages of twelve and fifteen
he had explored and made himself familiarly acquainted with what may
be called the public domain of arithmetic, trigonometry, astronomy,
optics, and mechanics, using not only the popular treatises, but also
the works of the highest name and authority on these subjects. For
instance, at the earliest of the ages we have mentioned, when first
interested in arithmetic, he passed almost at once to the study of
Newton's ``Arithmetica Universalis.'' Of the mode of his study of
science in these early years we are able to communicate a fact, which
appears to us of considerable value. We have heard from himself that
he attributes much of his subsequent progress in science to his habit
of never grudging any labour towards fixing clearly theorems in his
mind, by applying them to the solution of problems; and that
accordingly ``the questions for exercise,'' of various sorts, which
he used thus to resolve, while learning the elements of mathematics,
were very numerous indeed. As an example of this, we remember his
stating, that after being both astonished and delighted by the
demonstration of the existence of incommensurability, he was led often
to meditate upon it, and to engage for pleasure, in long numerical,
and usually, unwritten processes of approximation to the values of
surd roots; and this was before he was thirteen years of age. Neither,
with reference to his future lot, is the fact without interest, that
the possession of a telescope of his own enabled him at this period,
to be somewhat of a practical astronomer, and that the same manuscript
books which bear testimony to his early travails in the oriental
languages contain also records of some of his boyish observations of
eclipses of the moon, and of Jupiter's satellites, and of other
astronomical phenomena. From fifteen to seventeen, Newton's
``Principia,'' the application of algebra to geometry - the
differential, and in part, the integral calculus, together with such
original investigations as the study of these subjects naturally
suggested to such a mind as his, occupied most of the time which he
could spare to science from the collegiate entrance-course, which
necessarily made classical literature engage then a large share of his
attention. These studies, to which that of Laplace's
Méchanique Celeste, in the following year, is to be added, may be
said to have brought to a close that stage of his scientific progress
in which he is to be considered as predominantly a learner.
Soon after this occurred an event which doubtless exercised an
encouraging influence on the young aspirant in science: we allude to
his introduction to Brinkley, his illustrious predecessor in the chair
of astronomy. This introduction was marked by circumstances equally
honourable to both individuals, and which we cannot deny ourselves the
pleasure of relating. In the summer of 1822 W. R. H. was engaged, as
we have mentioned, in reading the Méchanique Celeste of
Laplace; an objection to a demonstration occurred to him, and a friend
(Mr. George Kiernan) induced him to write down his remarks on the
subject, and then soon afterwards showed them to Dr. Brinkley. The
perusal of these led to the expression of a wish on the part of
Dr. Brinkley, that Mr. K. would on the next opportunity introduce to
him their author: this kind intention was conveyed to W. R. H. at that
time staying with his uncle at Trim, in the autumn of the
above-mentioned year, and he determined to take advantage of it at the
approaching Christmas, which he was to spend in Dublin. In the mean
time he prepared a paper on ``Contact between Algebraic Curves and
Surfaces,'' (containing among other things an investigation of the
parabola osculating to a curve of double curvature,) and with this in
his hand, additionally to prove himself sensible of the honour to
which he was invited, and not unworthy of it, he came up to visit the
Observatory, and the celebrated mathematician who presided over it,
or, as he must then have felt, to approach an established throne of
science, and to receive audience of one whose name shed lustre on that
mighty seat of dignity, and whose word of approbation could confer
rank in the scientific world, as well as stamp the value of part
exertions, and encourage to continued efforts. The result was what
might have been anticipated by all who knew the character and
abilities of both. Dr. Brinkley, we need not say, received the young
Hamilton with kindness; he read and approved his paper, and showed the
interest he took in it by asking to see some of the investigations in
a more developed form: this request was complied with by Hamilton, who
in the following month laid before him a longer paper on the same
subject, entitled ``Developments.'' We have ascertained that both
papers still exist: they ought some day to see the light. From that
time forward for several years Hamilton was admitted to a personal
intimacy with the eminent man, to whom he was afterwards by so many
titles to be the worthy successor. How fully and gratefully this
privilege - a testimony equally to his personal as to his scientific
character - was estimated by the younger of the two is evinced in a
manner honourable to both parties, by a sentence at the close of the
second part of his paper on Caustics. This paper, which was the
product of the succeeding year, and the germ of that ``Theory of
Systems of Rays,'' which first gave general distinction to
Sir W. Hamilton's name, was presented in the year 1824 by
Dr. Brinkley, as its sponsor, to the Royal Irish Academy, of which he
was then president; it is thus concluded:-
``But whatever may be the opinions of others as to their value, I have
the pleasure to think that my paper is inscribed to the one who will
best be able to perceive and appreciate what is original;- whose
kindness has encouraged, whose advice has strengthened me;- to whose
approbation I have ever looked as a reward sufficient to repay me for
industry however laborious, for exertion however arduous.''
And, on the other hand, as manifesting the complete and generous
recognition by the elder savan, of the powers and attainments of his
youthful friend, we can record, from our distinct remembrance of the
fact being communicated to us by a mutual relative at a period
certainly anterior to the date last named, that Brinkley, speaking of
Hamilton, emphatically declared, ``This young man, I do not say
will be, but is, the first mathematician of his age.''
They who know how eminently qualified to judge, and how habitually
sober and truthful in speech, was Dr. Brinkley, will know the amount
of value to be attached to this expression of his opinion on such a
point, even though it be only reported as his conversational dictum.
Our pen would fain linger to depict with fuller illustration the
mutually reflected honour and regard of these two lights in the
hemisphere of science; but we must hasten on; suffice it to say, that
the receding star rejoiced to behold and to attest the culminating
lustre of his successor, and that, when in due time, he sank beneath
the horizon of the grave, a fitting close was put to the high
intercourse which had been theirs during life in an éloge
pronounced by that successor at the Royal Irish Academy, upon the
intellect, the labours, and the virtues of the illustrious
departed.2
We now return to the year 1823,- when Hamilton was in his eighteenth
year. It is an important era in the life of our subject, for it was
at this time that he began to employ himself in applying algebraic
geometry to optics; an application which he then supposed had not
been previously attempted by any other person. In this and the
succeeding year, pursuing, at the intervals of his studies for the
university examinations, the train of research we have indicated, he
arrived at numerous results of the highest interest; most of them
altogether new, though in some, as he afterwards found, he had been
partly anticipated by Malus; but in connection with which the great
feature was, that the method invented, and employed by him was so
comprehensive as to extend unlimitedly and with universal success over
the whole field of optics; ``dominant,'' to use the expression,
in reference to it, of the elegant historian of geometry M. Chasles,
``toute cette vaste theorie.'' These investigations, presented
in a general and abstract point of view, were embodied in the
manuscript essay on ``Caustics,'' to which we have before made
allusion, and which, after its communication to the Academy by
Dr. Brinkley, in December, 1824, was immediately referred by them to a
committee, consisting of Dr. MacDonnell, Mr. Harte, and Dr. Lardner.
This committee returned, in June, 1825, a report - our limits prevent
us giving more than its substance - which bore testimony to the
novelty and value of the results, and the analytic skill displayed in
the conduct of the investigations; but which recommended to the
author, as necessary to fit his memoir for publication, a fuller
development of the processes and reasonings by which his formulæ
and conclusions were arrived at. Acting on this advice of the
committee he employed himself at the intervals of collegiate study in
recasting and enlarging his paper, which was now anew presented to the
Academy under the title of ``Theory of Systems of Rays,'' on the 23rd
of April, 1827, and was published in 1828 as a paper in the fifteenth
volume of the Transactions of the Royal Irish Academy. The table of
``contents'' announced an intention of publishing in the third part of
the essay an application to Dynamics of the same general principle of
which the application to Optics was thus in part made public. The
second and third parts of the above-mentioned theory, in the form in
which they were presented to the Academy in 1827, remain as yet
unpublished; but many of the theorems which they contain, along with
many others, have been embodied in the three ``Supplements'' which
have appeared in subsequent volumes of the Irish Transactions, and in
the two essays, ``On a General Method in Dynamics,'' published by the
Royal Society of London.
Having been brought, in order of time, to its source, we have thought
it better thus summarily to present to the prospective glance of our
readers the whole history of the progress of this great work, by which
Sir William Hamilton has, in the opinion of those most competent to
judge, revolutionized mathematical optics, and established the means
of conquest to a similar extent over other territories of science; but
we must now revert to his personal history, of which our sketch must be
the more rapid, as we hope to find room for a popular view of the
contents of his works.
We cannot allow his collegiate career to pass by in an allusion. It
was in the summer of 1823, the year already named by us as dating the
commencement of his optical researches, that he entered college,- a
year later than had been intended, but illness had kept him back. We
well remember the rumour of the intellectual prowess of ``Hamilton the
prodigy,'' which preceded him to the courts of the university, and
appalled the courage of his future class-fellows. And, sooth to
say, never were expectations more fully realized, or rivals' fears
better justified. He began by gaining the first place at entrance,
upon a first mark in every book, and the first premium at the
subsequent examination in Hebrew. This commencement was only the
earnest of what followed. In a class which contained many competitors
of more than ordinary distinction, and in a division which usually
concentrated the best of them, he never once was beaten, but
uniformly, at every quarterly examination, obtained the chief honour
in both science and classics: on two occasions the honour was enhanced
by an optime, once for his answering in Greek, and afterwards at
the examination in Physics. To those who are unacquainted with the
conduct of examinations at Dublin, it may be necessary to state that
an optime is a judgment conferred there, only when the
examiner considers his answerer to have absolutely mastered the
subject of examination. We need scarcely add that the total number of
occasions on which this judgment has been awarded is very small, and
we believe it is a fact, that Sir Wm. Hamilton is the only individual
upon collegiate record who ever obtained two of them. To this list of
honours in the main courses of academic study, are to be added similar
successes at Hebrew and Catechetical Examinations, and the acquisition
of two Vice-Chancellor's prizes for English poems, of which the
subjects were ``The Ionian Islands,'' and ``Eustace St. Pierre.''
This uninterrupted, universal, and distinguished success produced, as
may be imagined, an excitement of admiration amongst his compeers, of
which we dare to say the glow has not yet altogether subsided in the
breasts of many. And in justice to both them and him we must attest,
that never were academic honours borne more meekly,- never had an
academic victor a richer addition to his crown from
``Generous rival's sympathy.''
And truly this series of triumphs demanded ``special wonder.'' Some
of our readers know what labour must have been expended for the
attainment of such success in every department of collegiate
distinction, especially when great expectations, on the part of
examiners, had to be satisfied. Now, let it be remembered that,
coincidentally with the exertions necessary to secure these results,
Hamilton carried on, as we have shown, his own original and laborious
mathematical investigations, and brought to the last stage - that of
the printing-press - his ``Theory of Systems of Rays.'' But,
moreover, we can state from our own remembrance the additional facts,
that he paid with regularity the tax upon his time which, to a man of
his attainments, the observance of college discipline in attendance
upon lectures, &c. must necessarily have been; and that even the
labours we have named did not so much absorb him as to prevent his
engaging in extra prolusions, scientific and literary, such as, for
instance, the calculation of an occultation of Jupiter, about which he
busied himself when a junior freshman, and his taking the principal
part in contributing to a series of essays, critical or imaginative,
yclept the ``Stanley Papers,'' which were for some time supplied
weekly to the breakfast-table of a small knot of youthful friends.
Neither is it to be thought that he was a mere recluse, or that his
energies were all of mind and none of body: eminently fitted in every
way, both to enjoy and to enhance the pleasures of intellectual
society, he was greatly in request as a companion - though doubtless
in this matter he felt himself oftener called upon to deny than to
indulge himself;- and pleasantly can we recall, as having been
fellow-votaries in the pursuit, his vigorous prosecution of gymnastics
at the academy of M. Beaujeu, where we have seen him as earnest about
circles, of which in his own person he flew along the circumference,
or about the ascent of perpendicular poles and slanting rope-ladders,
and the swinging between parallel bars, as ever he has been in
exploring the mysteries of ink-drawn curves and right lines, or in
ascending by the ladder of algebra to the specular heights of science.
During his passage through the university, William R. Hamilton
resided in Dublin, at the house of his cousin, Mr. Arthur
Hamilton, the barrister, a relative amply endowed with the
pleasantest and best qualities of a companion and friend, and
whose faithful affection supplied the loss which the subject of
our sketch and his sisters had sustained at an early age of both
their parents. In the beginning, however, of the summer of 1827,
he retired to the country - to the haunt of his childhood, at
Trim - in order to study for the two gold medals which then
crowned the honours of the undergraduate course at
Dublin,- (these honours, indeed, had never both been won by a
single aspirant, in competition with the main body, or pensioner
division, of the class; but in his case the double triumph was
looked forward to as not only likely, but certain,) - and to lay
in store to meet the subsequent requisition of the Fellowship
Examination. But his immediate plans and his ulterior destiny
were suddenly changed by a great and unexpected distinction; we
allude to his appointment at this time to the high and
responsible situation of Andrews' Professor of Astronomy to the
University of Dublin and Royal Astronomer of Ireland: an
appointment truly extraordinary - perhaps without parallel, when
considered as bestowed upon an undergraduate of
one-and-twenty,- but in this particular case, we think, equally
conferring honour upon the university authorities from whom it
emanated, as upon the individual whom it justly signalised. The
post in question had become vacant some months before by the
resignation of Dr. Brinkley, on his nomination to the Bishopric
of Cloyne. To place in the chair of such a man a successor
worthy of him, was an object which naturally demanded the anxious
care of those in whom the appointment was vested: and their
impartiality and public spirit were tested by the decision which
was called for from them upon many rival pretensions of no mean
order. Among their own body were fellows of high qualifications
and influence, desirous of the appointment; and from Cambridge
appeared as a candidate, with a reputation almost as high as he
now enjoys, George Biddel Airy, the present Astronomer Royal of
England. However, when the period approached at which the final
determination must be declared, what had been the expressed wish
of so many in conversation, the idea which the peculiar
eminencies of the individual naturally suggested, but which the
circumstances of his youth and standing as naturally
prevented being quickly put forward as a proposal, became a
subject of serious deliberation with the board. That
deliberation proved of so favourable a character, that his friend
and tutor, Dr. Boyton, to whom this circumstance became known,
immediately wrote to communicate the fact, and to advise him at
once to come up to town and propose himself as a candidate for
the appointment: a step which, before receiving this
encouragement, his modesty had withheld him from taking; although
he must have often heard himself mentioned by friends and
admirers in connexion with the vacant situation, as the
individual who would most appropriately fill it, an was therefore
abundantly entitled to look for it. He now felt that it was his
duty to act upon Dr. Boyton's letter, which was seconded by the
advice of his relatives, and in the course of a week from its
receipt the honour became his, with all its attendant pleasure
and congratulations, of being the successor of Brinkley in the
Professorship of Astronomy.
From that time the residence of Sir William Hamilton has been at
the Observatory, near Dublin. Here we have had the pleasure of
seeing him carrying on his life of high and abstract labour, and
of sharing occasionally the means of intellectual improvement, of
elevation and enjoyment, which his society lavishly supplies to
all who come within its influence. At first his new abode was
made a home to him by the presence of his sisters, whose
cultivated intellects and kindred tastes added to the uniting
bond of nature many strong and delightful links of sympathy. Of
this sisterhood it is impossible here to resist the temptation of
mentioning that one - E. M. H. - has been no unfrequent
contributor to the pages of the Dublin University
Magazine, where, we doubt not, many of our readers remember
poems discriminated by that signature, and remarkable for depth
and earnestness of thought and feeling, elevation of principle,
and force and vividness of expression; and from our pages we may
refer to the distinct volume which Miss Hamilton has given to the
world. During the Viceroyalty of Lord Anglesey, the Observatory
was additionally enlivened by the presence of two youthful sons
of the Marquess, who were for a short period pupils of Sir
William Hamilton, an advantage subsequently enjoyed for a longer
time, and with an ample result of intellectual profit to himself,
and honouring attachment towards his instructor by the Viscount
Adare, to whose name upon the roll of her nobility Ireland may
refer with pride, as that of one whose accomplishments and
principles add lustre to his rank. Upon the 9th of April, 1833,
Sir William Hamilton married Miss Helen Maria Baily, daughter of
the Rev. H. Baily, Rector of Nenagh, in the county of Tipperary,
and his home has since been enriched by the birth of three
children. For the whole of this period that home has been a
centre to which his high and various endowments of its occupant
have attracted, not only the scientific stranger, but numbers
from a wide circle, whose moral and intellectual tendencies have
been of a congenial nature; and consequently few scenes have been
oftener brightened by the mutual kindlings of genius, by the rich
interchange of thought, of imagination, and of wit, than the
Observatory at Dunsink. These social enjoyments are, however,
speaking strictly, of course occasional only; for, usually,
laborious study hold there its reign, and displays its insignia.
The works which we shall afterwards mention, as proceeding from his
pen, will show how hard and how successfully Sir William Hamilton
has been working in his retirement, as a scientific Author. As
Professor of Astronomy two spheres of exertion belong to him: that of
Lecturer upon the Science, in College, and that connected with the
practical working of the Observatory. Upon his duties as Lecturer
Sir William Hamilton entered with zeal, and has bestowed most
strenuous and persevering pains,- pains which we cannot but trust have
been rewarded by the propagation throughout the students of our
university of high and true views of the philosophy of science. In
these lectures he has exerted himself to present before his hearers,
not merely such information as a teacher of the ``use of the globes,''
or a university text-book might afford them, but, together with the
necessary illustrations of astronomy, such views of its connexion with
the other branches of science, and of its relations to the human
reason and imagination, as would enable them to possess a
comprehensive survey of their subject, and in the light of that survey
to pursue its study. Often have we been delighted to attend his
introductory lectures, full as they always have been of close logic,
of sound metaphysic, of truth united to poetry, and of a high moral
consecrating the whole, and all these elements fitted, by the
eloquence in which they were couched, to produce in his youthful
audience an ardent, and at the same time a wise enthusiasm for the
studies thus recommended.3
We can scarcely imagine a book that, to a particular class of
intellectual inquirers, would be more delightful or more serviceable,
than one formed by a collection of these introductory addresses: and
we cannot but entertain the hope, that Sir William Hamilton will one
day make this present to the young and generous aspirers after truth
among his countrymen.
To the practical working of the Observatory Sir William Hamilton, the
bias of whose genius is undoubtedly to pure mathematics, is not
naturally so adapted as to the other departments of scientific labour.
Here, however, he has, we know, diligently kept up the regular course
of observations and reductions; and in justice to him we feel bound to
protest against its being thought that the astronomer who presides
over it is singly responsible if the Dublin Observatory should not
hold a very high rank for the completeness and relative value of its
observations: for, besides the disadvantage of our climate, an
inadequate staff of assistants - at present there is only one - renders
the Observatory totally incapable of answering the requirements,
within the last ten years greatly multiplied, of the present state of
astronomical science. We have no doubt but that with a sufficient
body of assistants, the directing head of Sir William Hamilton would
soon raise this department to nearly as high a standing as it is
possible for it to attain.
Sir William Hamilton has been before the public eye as an active and
influential member of the British Association of Science. He joined
it so early as in 1832, when it assembled for its second meeting at
Oxford; and there, having been called upon, he laid before its members
a concise view of his optical method, and in behalf of the Royal Irish
Academy returned thanks, in a speech gracefully evincing a combined
pride of nationality, as an Irishman, and of compatriotism, as a
Briton. At Cambridge, the next year, his discovery of conical
refraction (which had been made in the interval, and of which we shall
give an account hereafter) was a principal feature of discussion, and
he received upon the occasion, from that university, the honour of
admission, in company with some other eminent men, to an
ad eundem degree of A. B. He took an active part, also, at the
meetings subsequently held at Edinburgh, Dublin, Bristol, Liverpool,
and Newcastle; but we can now only refer to that which passed with
such distinguished eclat in our own metropolis. Amongst its
conductors Sir William Hamilton held the prominent post of secretary,
in which capacity he delivered the Annual Address, afterwards
published in their Report, and to which (since our limits forbid us to
extract) we refer, as exhibiting a good specimen of his characteristic
eloquence and ability, in the development which it contains of the
power of the social sympathy as an impulse to science. It was during
this meeting that Lord Normanby, then Lord Lieutenant, seized, with a
happy tact, the opportunity of paying a most handsome compliment both
to Professor Hamilton and to Ireland, by conferring upon the foremost
representative of our nation's science, and in the face of the
assembled Association the honour of knighthood. The appropriate scene
was the library of our university. It was no slight addition to the
honour that Professor Whewell, in his speech at the banquet which
followed, should suggest, as a parallel remembrance, the fact that, a
hundred and thirty years before, a great man in another Trinity
College knelt down before his sovereign, and rose up Sir Isaac Newton.
Another distinction has since been conferred upon Sir William
Hamilton. We refer to his election, in the year 1837, to the
Presidentship of the Royal Irish Academy. This post was for many
years filled by Dr. Brinkley, both when Professor of Astronomy, and
afterwards when Bishop of Cloyne. Upon his death, in 1835, Sir
William Hamilton paid to the late Provost, Dr. Lloyd, the tribute of
his personal respect, by coming forward in the Academy and proposing
that the vacant seat of honour should be filled by a man, whose
combined pretensions, founded upon his personal character and
attainments, and his long-continued services to the science of his
country, called for such a rewarding recognition from the national
Academy. This eminent and excellent man too soon followed his
predecessor to the grave, again leaving vacant the presidential chair;
and it was upon this occasion that Sir William Hamilton successfully
aspired to the distinction; although he had to encounter the competing
claims of the Archbishop of Dublin and Professor Lloyd, who were at
the same time put in nomination. To the honour we speak of Sir
William Hamilton, besides his high scientific reputation, had some
peculiar titles. Long connected with the Academy - as an author, from
his boyhood - he had for many years taken a zealous interest in its
welfare; had enriched its Transactions with his valuable papers; had
been the means, as we happen to know, of inducing several of its most
distinguished members to join the body, and, perhaps may with truth be
said, to have been mainly instrumental in raising the institution
from a state of comparative neglect and inaction to that which it at
present enjoys of activity and repute. We may add, that for
discharging efficiently the duties of President he possesses eminently
the qualifications of wide and accurate knowledge, of a well-tempered
impartiality, and (we name an attribute especially valuable in the
leader of such a society) a generous aptitude to acknowledge and to
give the fullest meed of applause to the talents and services of his
fellow-labourers in literature and science: we have been struck by the
evidence of these merits exhibited in the published volume of the
Academy's Proceedings, containing addresses delivered by him on
presenting medals to Mr. Petrie, Dr. Apjohn, and Professor M`Cullagh.
We shall now essay the execution of that part of our undertaking, of
which we have already given notice, and to which some of our readers
may be looking forward as to matter more interesting than the
biographical portion of our sketch: we mean the presenting a concise
statement of the substance of the principal works of Sir William
Hamilton: in doing which, we shall endeavour in popular language to
give a true - though necessarily very general - answer to the inquiry
which has been often made of us in society - namely, what are the
nature and extent of those scientific labours and discoveries which
have gained for Sir William Hamilton the high reputation he enjoys?
In fulfilment of this part of our task, we shall first attempt to give
a slight and rapid outline of the researches which have been published
by Sir William Hamilton in his Essay on the Theory of Systems of Rays,
and in his Supplements to that essay, contained in the fifteenth and
following volumes of the Transactions of the Royal Irish Academy.
These researches may be said, upon the whole, to relate to
mathematical optics; and especially to contain a fundamental
conception, and general method and formula for the application
of Algebra (including the differential calculus) to the most varied
problems of that science. It is true, that before their publication,
many problems of this class, perhaps all that are required for the
most important practical applications, had been already resolved: many
valuable and elegant treatises upon the subject had been published;
and a tendency had shown itself, of late years, to assume the
algebraical form, and to adopt more or less the Cartesian method of
co-ordinates, which may be employed in all applications of algebra to
geometry. But with the exception of the profound Traité
d'Optique of Malus (the well-known discoverer of the polarization
of light by ordinary reflexion) this method of calculation, introduced
into algebraic geometry by Des Cartes, does not appear to have been
extensively and systematically applied to the solution of optical
problems, especially so as to take account of the three dimensions of
space. And the calculations of Malus, although symmetric, were so
extremely complex, that they not only conducted to true results with
difficulty, but even in some cases led (through a pardonable, because
scarcely evitable, inadvertency) into important error. In a word, it
appears that no appropriate general method had been
discovered for the treatment of optical problems. Either there were
special contrivances employed for the solution of particular
(though practically important) cases, which could not easily be
extended to new and more general questions: or when the universally
applicable method of co-ordinates was used, and the three dimensions
of space all kept in view, no adequate advantage was taken of anything
peculiar to the laws of light, but common to all those laws, so
as to combine, with the degree of generality aimed at, all such
facility and elegance as the nature of the subject might allow. A
method was to be found, or formed, which should effect for the
science of algebraical optics, what the method of Des Cartes
had done for algebraical geometry, or that of Lagrange for algebraical
mechanics.
A method of this kind has, we may assert, been invented by Sir W. H.,
and has been by him embodied in a new and fundamental formula, for the
study of optical systems. It seems to have occurred to
him,4
on abstract philosophical grounds, that in order to set out hopefully
in any general deduction of the consequences of the laws of the
propagation of light by rays, it was desirable to start from an
equally general induction respecting those laws themselves;
from the highest axiom (in the Baconian sense of the word)
which had yet been discovered respecting them. Now, such an axiom is
supplied by that celebrated and general result, which is called by
some the law of least action, and by others the law of the quickest
propagation of light. From this result of induction, admitted
to be valid, at least as such, by the adherents of the two rival
theories, by those who suppose light to consist of particles emitted,
and by those who hold it to be communicated by transmitted vibrations,
Sir W. H. accordingly sets out. And as it expresses that a
certain quantity (which in one theory is the action, and in
the other theory is the time expended by light in its
propagation along any bent or curved path, from one point to
another), is, under certain conditions, invariable - namely,
when the two extreme points are fixed; so he inquires
how the same quantity varies under certain other
conditions - namely, when the extreme points are changed. And the
expression which he obtains for the law of such new variation, becomes
his fundamental formula, his ``equation of the characteristic
function;'' deduced, indeed, as has been stated, from the most general
known law respecting the successive directions of any one path of
light, but reciprocally including that law, and adapted rather to the
study of optical systems, than to that of any single ray.
It would be impossible to enter here into any further details
respecting the precise nature of this very general and abstract
conception. But we may be permitted to illustrate its bearing by a
single elementary example. It has long been known that when light,
setting out from any given luminous point, is reflected at any second
point upon a given plane mirror, and reaches, after this reflection,
any third point; then, first, the reflected ray proceeds as if
from a given image of the first point, situated behind the mirror;
and, secondly, the whole bent path traversed by the light, is
equal to the distance of the last point of that path from the image of
the first point. Now, the general method of Sir W. H., when applied
to this simple case, connects these two old theorems together, and
shows that the former might have been deduced as a consequence from
the latter. In other words, the knowledge of the law of the
length of the bent path, in this and other cases of reflexion of
light, conducts, according to his general method, to the knowledge of
the laws of the directions of the extreme parts of that path.
And analogous connexions are established by him for refraction,
ordinary or extraordinary.
Among the results of this general view or method may be
mentioned, the facility with which it conducts to a proof of the
existence and determination of the properties of a certain series
of surfaces, which cut perpendicularly the rays of any ordinary
system, reflected or refracted any number of time by any
combination of mirrors, lenses, and atmospheres. It is true that
the theorem of the general existence of such surfaces had been
distinctly perceived by Huyghens, and had even formed an essential
element in his theory of light; since those surfaces were, in
fact, the waves, which in that theory were considered as
each marking out, for some one moment of time, the boundary of
the spaces traversed by the light in all the several rays of the
system. Indeed, in this now celebrated, though for a long time
forgotten theory of Huyghens, the rays were derived from the
perpendicular wave-surfaces, rather than the latter from the
former. But the mathematical deduction of the theorem of the
general existence of such perpendicular surfaces, from the
consideration of the rays as mathematical lines, and from the
purely mathematical laws of reflexion and refraction (abstraction
being made of every physical hypothesis), would seem to have been
not exempt from difficulty, in a recent state of optical science;
since Malus, in the important Treatise above referred to, was led
to deny the fact of such existence, even for the very simple case
of two successive reflexions. And although Dupin had confirmed
the theory of Huyghens, before the publication of Sir W. H.'s
first essay, yet Plana, one of the most eminent Italian analysts,
in a letter published in the Correspondence5
of Professor Quetelet, of Brussels, later by several years than
the researches of Dupin, avowed himself unable to trace the error
of Malus to its source, or to point out the mode of refuting it.
Sir W. H.'s answer, published in the same
Correspondence,6
met, and removed this difficulty on its own ground; but really,
to any one who had caught the spirit of his method, and had
understood his fundamental formula (which was not then known in
Italy), the mathematical difficulty could not have arisen, nor
could the mathematical existence of the surfaces in question have
possibly eluded notice. As a matter of personal, though it
cannot claim to be of historical interest, we may be permitted to
mention what our acquaintance with the subject of the present
sketch enables us to do, that the controverted theorem above
referred to, was arrived at in his own investigations, during his
first collegiate years, and before he had any knowledge of the
researches of Huyghens, Malus, or Dupin.
But the published results which Sir W. Hamilton has deduced from
his general method, are by no means limited to new proofs of
previously known theorems, original or interesting as such proofs
may sometimes be; they are, so far as we have been able to
ascertain, for the most part entirely new. Our limits compel us
to give here a selection, or sample, rather than a catalogue.
But we cannot avoid alluding to the theorems respecting
osculating focal reflectors and refractors, ordinary and
extraordinary, concerning which our author has established a
series of new theorems, analogous in part to the known theorems
respecting spheres osculating to other surfaces: the discovery of
the principal foci, and principal rays, or axes, of a reflected
or refracted system generally, including, as infinitely
particular cases, those foci and axes of the same kind which
alone had previously been treated of; the consequent general
theory of optical images and aberrations, with its application to
instruments of revolution, of which last application, indeed,
only an outline has as yet been published (in the Transactions of
the Mathematical Section of the British Association, at the
Cambridge meeting), and the prediction of conical refraction.
This last result may, perhaps, properly receive a somewhat fuller
notice here, because it has attracted more interest than the rest
in England and elsewhere.
The law of the reflexion of light at ordinary mirrors, appears to
have been known to Euclid; that of ordinary refraction at a
surface or water, glass, or other uncrystallised medium was
discovered in a much later age by Snellius: Huyghens
discovered, and Malus confirmed, the law of the extraordinary
refraction produced by one-axed crystals, such as Iceland spar;
and finally, the law of the extraordinary double refraction at
the faces of biaxal crystals, such as topaz or arragonite, was
found in our own time by Fresnel. But even in these cases of
extraordinary or crystalline refraction, no more than two
refracted rays had every been observed, or even suspected to
exist, if we except a theory of Cauchy, that there might possibly
be a third ray, though probably imperceptible to our
senses. Sir W. H., however, in investigating by his general
method the consequences of the law of Fresnel, was led to
conclude that there ought to be, in certain cases, which he
assigned, not merely two, nor three, nor any finite number, but
an infinite number, or a cone of refracted rays
within a biaxal crystal, corresponding to and resulting
from a single incident ray; and that, in certain other
cases, a single ray within such a crystal should give rise to an
infinite number of emergent rays, arranged in a certain other
cone. He was led, therefore, to anticipate from theory two new
laws of light, to which he gave the names of INTERNAL AND
EXTERNAL CONICAL REFRACTION. This anticipation he announced to
a general meeting of the Royal Irish Academy, on the occasion of
presenting to that body the Third Supplement to his Theory of
Systems of Rays, in which he had embodied his reasonings upon the
subject, on the 22nd of October, 1832. On the following day he
requested his friend, Professor Lloyd, to undertake an
experimental investigation, with a view to effect the actual
exhibition of the new phenomena thus predicted. It was
difficult, for some time, to procure crystals of the requisite
size and purity; but these, and other difficulties, were
surmounted in perfectly establishing, by experiment, what Sir
W. H. had predicted from theory.
The result excited at the time a very considerable sensation among
scientific men in England and on the Continent; it was thought a happy
boldness to have thus seized and brought into view, by dint of
reasoning, a new class of phenomena, to which nothing similar had been
before observed, and which even seemed, in the words used by an
eminent English philosopher, to be ``in the teeth of all analogy.''
At the Cambridge meeting of the British Association, in 1833, the
attention of the mathematical and physical section was largely given to
the subject: and Herschel, Airy, and others, spoke warmly in praise
of the discovery. In the introductory discourse with which the
proceedings of that meeting were opened, Professor Whewell made it a
topic, and expressed himself in the following words - ``In the way of
such prophecies, few things have been more remarkable than the
prediction, that under particular circumstances, a ray of light must
be refracted into a conical pencil, deduced from the theory by
Professor Hamilton, and afterwards verified experimentally by
Professor Lloyd.''7
Previously, in the same year, Professor Airy had publicly recorded his
impression upon the subject as follows - ``Perhaps the most remarkable
prediction that has ever been made, is that lately made by Professor
Hamilton.''8
More lately, Professor Plücker, of Bonn, in an article on the
general form of luminous waves, published in the nineteenth volume of
Crelle's Journal, has used these words - ``Aucune experience de
physique a fait tant d'impression sur mon esprit, que celle de la
refraction conique. Un rayon de lumiere unique entrant dans un crystal
et en sortant sous l'aspect d'un cone9
lumineux: c'etait une chose inouie et sans aucune analogie.
Mr. Hamilton l'annonça, en partant de la forme de l'onde, qui
avoit été deduite par les longs calculs d'une theorie
abstraite. J'avoue que j'aurois désesperé de voir
confirmé par l'experience un resultat si extraordinaire, predit
par la seule theorie que la genie de Fresnel avait nouvellement
créé. Mais Mr. Lloyd ayant démontré que les experiences
etaient en parfaite concordance avec les predictions de Mr. Hamilton,
tout préjugé contre une theorie si merveilleusement soutenue,
a dû disparaitre.'' And it seems to be in part to this subject
that reference is made in a passage of the article, attributed to Sir
John Herschel, on the inductive sciences, in the last June number
(page 233) of the Quarterly Review, where mention is made of a
sound induction enabling us to predict, bearing not only stress, but
torture: of theory actually remanding back experiment to read her
lesson anew; informing here of facts so strange, as to appear to her
impossible, and showing here all the singularities she would observe
in critical cases, he never dreamed of trying.
Be that as it may, it is our pleasing duty as Irishmen to acknowledge
the cordiality of the reception which the intellectual exertions of
the subject of this sketch has met with in Great Britain, and in
foreign countries. Herschel led the way, by giving, as the concluding
sentence of his Treatise on Light, in the ``Encyclopædia
Metropolitana,'' a most handsome notice of the Theory of Systems of
Rays, then only passing through the press of our academy, but known by
private circulation. Airy, at the Cambridge meeting, spoke of our
friend as having rendered optics a new science. Whewell, in his
History of the Inductive Sciences, and Babbage, in his Ninth
Bridgewater Treatise, have assigned no unimportant place to the
prediction of the conical refractions. An appreciation of what had
been done in this matter was marked, not only here, by the award to
Sir W. Hamilton from the Royal Irish Academy, of their Cunninghame
Gold Medal, but also by his receiving, from the Royal Society of
London, one of the Royal Gold Medals entrusted to their disposal by
King William the Fourth. Besides being a member of many scientific
societies in England and Scotland, and welcomed to personal intimacy
with the most eminent men of science there, he has received many
diplomas, and other marks of attention and respect from abroad. He is
a member of the American Academy of Arts and Sciences; of the
Academies of Berlin, Turin, and St. Petersburgh; and we believe of
others, which we shall not now try to recollect. But the mention of
the Imperial Academy of St. Petersburgh reminds us of his labours in
another direction, of which the diploma from the Russian Society was
more especially designed to attest their view of the importance.
Sir W. H., though from motives, we believe, of private convenience, he
has not hitherto allowed himself to be proposed as a member of the
Royal Society of London, has taken occasion to express his high
respect and cordial goodwill towards that society, not only in his
inaugural address to our academy, on being elected its president, but
also by contributing, in imitation of his predecessor, Dr. Brinkley,
some papers to the Philosophical Transactions. The papers thus
published by him in London, are entitled, ``On a General Method in
Dynamics;'' and they contain a system of complete and rigorous
integrals of the celebrated differential equations of motion of a
system of bodies, which had for so long a time tormented the
scientific world of Europe: these integrals having been discovered by
the application to this important question, of the same general
algebraical method which he had already applied to optics. Indeed, as
we have before recorded, a notice of the applicability of the method
to dynamics, was very early and distinctly given in his first
contribution to the Transactions of the Royal Irish Academy; but the
subject seems to have passed from his thoughts, till after he had
completed the investigations respecting conical refraction. He then
returned to it, and the papers above mentioned were drawn up. They
have, we know, been thought important upon the Continent: and we
believe that we are safe in saying, that the great German
mathematician, Jacobi (author of the Nova Fundamenta Functionum
Ellipticarum Theoriæ), has considered it worth his while to
translate largely from them, and to accompany his translations with
copious comments, though we cannot at present procure the work in
which his remarks are contained. And it was for these particular
contributions to science that Sir W. Hamilton received the honour,
rare in these countries, of being elected a corresponding member of
the St. Petersburgh Academy; the diploma assigning as the reason, in
Latin words which we forget, ``that he had deserved extremely well of
science, with respect to the accomplishment of the integration of the
general equations in dynamics.''
Many other investigations on scientific subjects have been published
by Sir W. H., either fully or in outline, in the Transactions and
Proceedings of the Royal Irish Academy, in the Transactions of the
British Association, in the London and Edinburgh (now entitled also
Dublin) Philosophical Magazine, and perhaps through other channels of
publication. Thus, at the Bristol meeting of the Association, he gave
an account (very brief, it is true) of a certain ``Calculus of
Principal Relations,''10
already announced by him in a still briefer manner
before,11
which includes as particular cases what he had done in optics and
dynamics, and has for its object to integrate the differential
equations to which the calculus of variations conducts, by combining,
in a peculiar way, the principles of the latter calculus with those of
the calculus of partial differentials. At the same meeting he
presented, by invitation, a Report (since published by the
Association) on the Researches of
Mr. Jerrard,12
respecting Equations of the Fifth Degree, in which, while he
acknowledged the great ingenuity of those researches, he maintained
that they had not succeeded in effecting their chief object - namely,
the solution of equations of degrees higher than the fourth. Sir
W. H. has since published, in the Transactions of the Royal Irish
Academy,13
an elaborate Essay on Equations of the Fifth Degree, in which he
confirms, by reasoning of his own, the argument, or at least the
conclusion, of Abel (an analyst of Norway, whose early death has often
been regarded as one of the greatest losses sustained by science in
recent times) - namely, that a general solution of such equations, by
any combination of radicals and rational functions, is impossible. Of
this essay, we know that it has been considered by a very high
scientific authority, as definitely settling the long-vexed and
interesting question upon which it treats; a result which the doubtful
expressions used in Professor Peacock's
Report14
prove not to have been attained by Abel's ``Demonstration;''
and although this Essay of our friend bears the modest title, ``On the
argument of Abel,'' we believe no one of his works displays more fully
his great powers of original investigation, and his familiarity with
the principles of the most abstract analysis. To give even the titles
of all his shorter papers would exceed our limits, on which we have
already trespassed; and we shall therefore conclude this part of our
sketch by saying a word or two upon a treatise of a peculiar and
semi-metaphysical kind, which he has published in the Transactions of
the Academy, on ``Algebra Considered as the Science of Pure
Time.''15
Sir William Hamilton, with his strong propensity to generalize, to
take of every subject the most central view, and to look not only in
physical but even in mathematical science, for somewhat which may
interest the imagination, and be of kin to poetry, has not escaped the
temptation to indulge in metaphysical reading and speculation, more
than is very common, or perhaps quite approved of among
mathematicians. Though a firm believer in the Christian revelation,
and an attached member of the Church of England, he has allowed
himself to be charmed, not only by Berkeley and Coleridge, but by
Kant. And though we suppose that he would disclaim the implicit
adoption of the teaching of any of the three, who indeed differ widely
among themselves, yet we regard him as having made a decidedly Kantian
movement, when he conceived and published that view of algebraic
science, including the various calculi, to which we have just now
referred. Kant's pure intuitions of space and time, now made familiar
to the English reader by ``Whewell's Philosophy of the Inductive
Sciences,'' had enjoyed very unequal fortunes as compared with one
another. The intuition of space was easily admitted by all whose
leanings were in this direction, to be the subject-matter of geometry
as a science. But the intuition of time was not (we believe) claimed
by Kant, or by his followers16
as being, in any similar way the ground of any pure mathematical
science; except so far as the doctrine of
motion17
may be such, which however seems to involve other elements. The
pendant to the Kantian view of geometry appears to have been supplied
by Sir William Hamilton's conception of algebra; which, as a science,
rests according to him, essentially on the pure intuition of time. It
must be observed, to guard against misapprehension, that he seems to
regard this pure intuition, or original mental form, as ``closely
connected, and in some part coincident with the notion of
continuous progression;'' and that he is careful to distinguish
his science of pure time ``on the one hand from all actual
outward chronology, or collections of recorded events and phenomenal
marks and measures, and on the other hand from all dynamical science,
or reasonings and results from the notion of cause and effect.''
Unless some such view be adopted, and the conception of time (thus
generalised and guarded) be admitted as a fundamental element of
algebra, it will indeed by hard, as he has shown, to maintain that
algebra is a Science at all; and we shall be almost driven to
concede what is contended for by some eminent men, that algebra is
rather to be accounted an Art or a Language; or at least
that its theorems are nothing else than either, on the one hand,
practical rules, or on the other hand, laws of symbolism. We do not
feel competent to offer an opinion of our own upon the subject, and
doubt whether the question raised by our countryman will ever be
entirely decided. It seems to be connected with some of those deep
and subtle strifes of intellect, which divide speculative minds at
this day, as much, if not as warmly, as in the oldest times.
The train of circumstances which led to the publication of his
view we may mention as evincing the friendly spirit by which he
has always been actuated towards his fellow-labourers in the
field of science. His old college-companion and competitor,
John T. Graves Esq. (now of the Inner Temple, London) had
published, in the Philosophical Transactions for 1829, a paper
upon imaginary logarithms, in which conclusions were contained
not easily reconcilable with generally received principles, and
which met at the time with a good deal of opposition from eminent
quarters. Sir William Hamilton records, that ``in reflecting on
the important symbolic results of Mr. Graves, and in attempting
to explain to himself those remarkable symbolisms, he was
conducted to his theory ``of Conjugate Functions, or Algebraic
Couples,'' which he then gave to the world, in confirmation of
the conclusions of his friend: and it was to this theory of
Conjugate Functions that he afterwards prefixed the more general
essay, of which we have been speaking, as calculated to throw
additional light upon Mr. Graves's paper, as well as to suggest a
true theory for the science at large. For a distinct view of the
object aimed at in that essay, we refer the reader from our
slight hints to the general introductory remarks by which it is
preceded: those remarks admirably fulfil the intention of their
author. We have nowhere met with a piece of composition more
remarkable for lucid arrangement of thoughts, and for accuracy
and symmetry of expression.
Such is the sketch which we promised of the contents of Sir
William Hamilton's principal works. Since the publication of the
last of them, a longer pause than had been usual has succeeded,
and we had begun to ask, what is Sir William Hamilton doing?
Every one, indeed, must know that an indefinite series of
productions equal in weight and originality to those we have
passed in review is not to be expected from any intellect; but as
we were aware that our friend's stores of scientific work, either
completed or planned, were by no means exhausted, a moderate
degree of impatience, we own, tempered by some anxiety lest
previous over-labour might be the cause of the cessation, was
rising within us. We have, therefore, hailed with pleasure the
indications, in late numbers of the Philosophical Magazine, of
renewed activity on his part in the way of publication; these
re-assure us as to his being in working order: and, freed from
apprehension on this score, we will not refrain, in regard to the
projects of a higher stamp, which we know Sir William Hamilton to
have had on hand, from making an appeal that they be not allowed
to lie too long without being brought to book,- ad
umbilicum. We are the more induced to say this, because we are
free to confess, as to our friend, that we do not consider him
exempt from our national sin of procrastination. Should
curiosity tempt him to read our notice of himself, we are sure
that after the praise which we have felt it his due to give, he
will be quite refreshed by the hint of a fault; and we trust
that, if conscience second us, he will in gratitude set himself
to act upon our suggestion. From the publication of some of his
completed papers, we know that he has been hindered by the desire
not to press with disproportionate weight upon the limited funds
applicable by the Royal Irish Academy to the expenses of
printing.
And now, one word upon a subject which we could have wished to
avoid, and for touching upon which we are afraid we shall incur
our friend's displeasure, but upon which we have too strong a
feeling to allow us to be silent. We allude to what we consider
the very inadequate income upon which Sir William Hamilton has to
live: inadequate as it appears to us, both to his individual
claims and the station which he fills. Sir William Hamilton is
the possessor of no patrimonial fortune, neither has he been
enriched by marriage: he has been restrained from entering into
the ministry of a church to which he is conscientiously attached,
and to the most lucrative dignities of which he might naturally
have looked forward, by a fear, which does him the highest
honour, if not of any incompatibility between the functions of a
clergyman and those which he now discharges, yet at least of
affording ground of offence on this score to weaker brethren, or
to enemies of the church: he has been precluded, we believe
indeed by compact with the university, but at all events, we will
say, by a due consideration of his present standing, and by
justice to his own intellect and to the rightful claims upon it
of the scientific world, from aiding any longer his pecuniary
resources by the task of tuition: and upon a net income of less
than six hundred a year, he has not only to support and provide
for his family, but to maintain, for the credit of himself, his
university, and his country, a hospitality upon which the demands
are rendered the greater by his eminent merits and extended
reputation. We know too well the dignity and unworldliness of our
friend's character, to this that he will remonstrate on this
subject, concerning which, intimate as we have been, we have
never heard from him a word of complaint; we also know that in
this hurrying world such a character and such conduct are too apt
to be neglected or admired, rather than advocated and rewarded;
and therefore, feeling that the occasion is exactly one upon
which a friend's voice is alone likely to break a silence which
ought not to last, we have taken the present opportunity of
speaking our word of appeal; and we trust that, humble as it the
quarter from which it proceeds, it will not be addressed in vain
to the justice and the liberality of authorities, who have at
heart, we know, the reputation of our national institutions, and
upon whom will be reflected a lasting credit from any set which
shall brighten the life of a man now certain of holding a
distinguished place in the scientific annals of his country.
The outward form of our friend is the artist's share; perhaps,
however, we shall not trespass beyond our dominion by adverting
to the ``ample dome'' which Sir William Hamilton's head
presents,- its wide compass, its full-orbed development, its
lofty elevation,- a physical type, and if the phrenologists be
right, an organic index of the capacious mind, with its
harmoniously balanced faculties, there inhabiting. Our task we
will now bring to an end by grouping, with as much faithfulness
as we can, the features of his mind and character.
Professor Sedgwick, when President of the British Association at
Cambridge, illustrated his own liberal spirit - every one knows his
manifold ability to judge - by referring publicly to Sir William
Hamilton as ``a man who possessed within himself powers and talents
perhaps never before combined within one philosophic character.''
Of these powers, however, we believe that we may rightly name that of
generalization, as the power which holds the predominant place, and is
possessed by Sir William Hamilton in a degree which has been
seldom equalled. It is that of which his mathematical works are
eminently the product, and which makes mathematics to him a region
over which metaphysical thought bears a presiding sway, and where
imagination can successfully exercise her creative and combining
energy, in devising new relations and higher laws. That he perceives
the philosophical obligation afterwards to authenticate these
relations and laws by induction, and to demonstrate them by the
employment of a strict deductive process, and that he has the power
also to fulfil this task, and the disposition to expend upon it the
necessary amount of labour, frees him from the imputation of
deficiencies which have often depreciated the fame and diminished the
usefulness of those explorers in the high priori path, with
whom the powers we have above referred to, of generalization and
active imagination, were not similarly balanced; but who, after all,
because they possessed these highest and most living faculties, will
ever be allowed to stand in the first rank of scientific genius. It
is this possession by Sir William Hamilton of imagination and
metaphysical insight, in addition to the powers more commonly the
exclusive property of men of science, which have made his mind and
conversation a source of peculiar interest, as we know has been the
case, to Coleridge and to Wordsworth, the latter of whom has often, in
our hearing, testified the admiration and regard he entertains towards
our countryman.
These high powers of Sir William Hamilton are served by a memory of
unusual vigour; which also furnishes to his conversation, from the
various fields of literature, nature, art, and life, felicitous
allusion, appropriate example, and illustrative anecdote. That
conversation, exception being made that for some audiences it is too
wide and elemental in its general character, receives almost every
additional intellectual charm from his natural eloquence, from
language - his mastery over which is complete - the most varied and
often original, from a lively fancy, a free discursiveness, and a
clear logic: while the
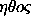 of the man causes it
to shine with a light refracted from qualities still more excellent
and amiable;- a buoyant cheerfulness, an ingenuous simplicity, a
kindly human-heartedness, glad to praise, and glad to receive the
reward of genuine approbation, a patient candour, a singleness of
fidelity to truth, a love for all that is intellectually or morally
noble, and an habitual reverence for every divinely-imposed restraint
upon the play of fancy and the speculations of intellect.
of the man causes it
to shine with a light refracted from qualities still more excellent
and amiable;- a buoyant cheerfulness, an ingenuous simplicity, a
kindly human-heartedness, glad to praise, and glad to receive the
reward of genuine approbation, a patient candour, a singleness of
fidelity to truth, a love for all that is intellectually or morally
noble, and an habitual reverence for every divinely-imposed restraint
upon the play of fancy and the speculations of intellect.
The poetical productions of Sir William Hamilton are in our eyes of
considerable value: more perhaps, indeed, as beautiful emanations of
his character, evidencing the strength and generousness of his
affections, and the loftiness of the aspirations and communings of his
spirit, than as works of poetic art: yet many of them, we think, prove
that had he devoted his powers to this art as a study, he might have
gained a high place among our poets. We annex one of his sonnets,
chosen not so much to exhibit to advantage his powers of rythm and
expression, as to accredit our testimony to the exaltation and
generosity of his nature.
In politics Sir William Hamilton has always been a Conservative of
enlarged views and steadfast principles, which he has not shrunk from
publicly maintaining. As to his religion, we are deeply gratified to
have abundant warrant for believing that in conviction, in feeling,
and in life he is an attached member of the Church of England, a
sincere and devout Christian.
We had thought to conclude our memoir by designating him as ``the
Irish Lagrange;'' flattering, however, to his scientific merits as the
parallel possibly might be, his own name, we will believe, is his most
fitting and honourable designation - Sir William Rowan Hamilton - a
name which, we doubt not, will live a long life of scientific
reputation, and be proudly remembered by his country as that of a
great and a good man. But listen to his own sublime and holy
aspiration!
O brooding Spirit of Wisdom and of Love,
Whose mighty wings even now o'ershadow me,
Absorb me in thine own immensity,
And raise me far my finite self above!
Purge vanity away, and the weak care
That name or fame of me may widely spread:
And the deep wish keep burning, in their stead,
Thy blissful influence afar to bear,-
Or see it borne! Let no desire of ease,
No lack of courage, faith, or love, delay
Mine own steps on that high thought-paven way
In which my soul her clear commission sees:
Yet with an equal joy let me behold
Thy chariot o'er that way by others roll'd!
Notes:
1Mr. J. Hamilton is the author of an essay printed
in the Transactions of the Royal Irish Academy ``On the Punic passage
in Plautus.''
2In November, 1835. Of this tribute the Academy, as
we learned from its minutes, requested afterwards to be furnished with
a transcript, which might remain amongst its records; but we have
ascertained with regret that the author, for some reason, was unable
to comply with the request. The subsequently adopted plan of printing
the proceedings at the academical meetings, for distribution among the
members, is of great value, as securing the preservation of such
memorials.
3It is stated in a note in
Blackwood's complete edition of Mrs. Hemans' works that her beautiful
poem, ``The Prayer of the Lonely Student,'' was written after hearing
one of Sir William Hamilton's Introductory Lectures. The poem takes
up the high religious theme at which the conclusion of the lecture
reverentially glances. Sir William Hamilton and his sisters enjoyed
the personal friendship of Mrs. Hemans; we happen to know that it was
a flower sent to her room of sickness, from the garden of the
Observatory, which suggested her exquisite lines, ``To the Blue
Anemone.''
4See the article contributed by Sir W. H. to the fourth
number of the Dublin University Review (October 1833,
Milliken), entitled, ``On the paths of Light and of the Planets.''
This article, as well as several other papers, by Sir W. H., has been
translated into French, and published by Professor Quetelet, of
Brussels.
5Tome VIII.
Livraison 2, page 99. Il y a dans l'analyse precedente un vice
radical que echappe a toutes mes reflexions.
6Tome VIII. Livraison 1, page 27.
7``Report of the Third Meeting of the
British Association for the Advancement of Science, held at Cambridge
in 1833.'' Page xvi.
8``London and Edinburgh Philosophical Magazine.''
June 1833, p. 420.
9As we understand the
matter, the interior cone emerges as a cylinder.
10Report of the Sixth Meeting of the
British Association for the Advancement of Science, held at Bristol in
1836. Vol. V. Notices, p. 41.
11In
the introductions to his Essays on Dynamics, published in the
Philosophical Transactions.
12Mathematical
Researches, by George B. Jerrard, A.B. Strong, Bristol.
13Vol. XVIII.
14Report on the
Recent Progress and Present State of Certain Branches of Analysis.
Report of the Third Meeting of British Association. We allude to the
following expressions at pages 311 and 312 - ``Some parts of it are
obscure, and not perfectly conclusive.'' ``If the demonstration of
Abel should be likewise admitted.''
15Vol. XVII. Part ii.
16Mr. Semple in the ``Metaphysic
of Ethics, by Immanuel Kant,'' speaks of our understanding of how
geometry and algebra arise, by the theory that space and time are
intuitions a priori. This work was published (at Edinburgh) in
1836; Sir W. Hamilton's essay in 1835.
17Also
erklärt unser zeitbegriff die möglichkeit so vieler
erkenntniss a priori, als die allgemeine bewegungslehre, die nicht
wenig fruchtbar ist darlegt. - Kant. C. d. r. V.
Links:
D.R. Wilkins
(dwilkins@maths.tcd.ie)
School of Mathematics
Trinity College, Dublin
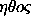 of the man causes it
to shine with a light refracted from qualities still more excellent
and amiable;- a buoyant cheerfulness, an ingenuous simplicity, a
kindly human-heartedness, glad to praise, and glad to receive the
reward of genuine approbation, a patient candour, a singleness of
fidelity to truth, a love for all that is intellectually or morally
noble, and an habitual reverence for every divinely-imposed restraint
upon the play of fancy and the speculations of intellect.
of the man causes it
to shine with a light refracted from qualities still more excellent
and amiable;- a buoyant cheerfulness, an ingenuous simplicity, a
kindly human-heartedness, glad to praise, and glad to receive the
reward of genuine approbation, a patient candour, a singleness of
fidelity to truth, a love for all that is intellectually or morally
noble, and an habitual reverence for every divinely-imposed restraint
upon the play of fancy and the speculations of intellect.