From `A Short Account of the History of Mathematics' (4th edition, 1908) by W. W. Rouse Ball.
Leaving for a moment the English mathematicians of the first half of the eighteenth century we come next to a number of continental writers who barely escape mediocrity, and to whom it will be necessary to devote but few words. Their writings mark the steps by which analytical geometry and the differential and integral calculus were perfected and made familiar to mathematicians. Nearly all of them were pupils of one or other of the two elder Bernoullis, and they were so nearly contemporaries that it is difficult to arrange them chronologically. The most eminent of them are Cramer, de Gua, De Montmort, Fagnano, l'Hospital, Nicole, Parent, Riccati, Saurin, and Varignon.
Guillaume François Antoine l'Hospital, Marquis de St.-Mesme, born in Paris in 1661, and died there on Feb. 2, 1704, was among the earliest pupils of John Bernoulli, who, in 1691, spent some months at l'Hospital's house in Paris for the purpose of teaching him the new calculus. It seems strange, but it is substantially true, that a knowledge of the infinitesimal calculus and the power of using it was then confined to Newton, Leibnitz, and the two elder Bernoullis - and it will be noticed that they were the only mathematicians who solved the more difficult problems then proposed as challenges. There was at that time no text-book on the subject, and the credit of putting together the first treatise which explained the principles and use of the method is due to l'Hospital; it was published in 1696 under the title Analyse des infiniment petits. This contains a partial investigation of the limiting value of the ratio of functions which for a certain value of the variable take the indeterminate form 0 : 0, a problem solved by John Bernoulli in 1704. This work had a wide circulation; it brought the differential notation into general use in France, and helped to make it known in Europe. A supplement, containing a similar treatment of the integral calculus, together with additions to the differential calculus which had been made in the following half century, was published at Paris, 1754--56, by L. A. de Bougainville.
L'Hospital took part in most of the challenges issued by Leibnitz, the Bernoullis, and other continental mathematicians of the time; in particular he gave a solution of the brachistochrone, and investigated the form of the solid of least resistance of which Newton in the Principia had stated the result. He also wrote a treatise on analytical conics, which was published in 1707, and for nearly a century was deemed a standard work on the subject.
Pierre Varignon, born at Caen in 1654, and died in Paris on Dec. 22, 1722, was an intimate friend of Newton, Leibnitz and the Bernoullis, and, after l'Hospital, was the earliest and most powerful advocate in France of the use of the differential calculus. He realised the necessity of obtaining a test for examining the convergency of series, but the analytical difficulties were beyond his powers. He simplified the proofs of many of the leading propositions in mechanics, and in 1687 recast the treatment of the subject, basing it on the composition of forces. His works were published at Paris in 1725.
Pierre Raymond de Montmort, born at Paris on Oct. 27, 1678, and died there on Oct. 7, 1719, was interested in the subject of finite differences. He determined in 1713 the sum of n terms of a finite series of the form
a theorem which seems to have been independently rediscovered by Chr. Goldbach in 1718. François Nicole, who was born in Paris on Dec. 23, 1683, and died there on Jan. 18, 1758, published his Traité du calcul des différences finies in 1717; it contains rules both for forming differences and for effecting the summation of given series. Besides this, in 1706 he wrote a work on roulettes, especially spherical epicycloids; and in 1729 and 1731 he published memoirs on Newton's essay on curves of the third degree.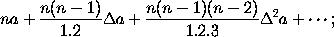
Antoine Parent, born at Paris on Sept. 16, 1666, and died there on Sept. 26, 1716, wrote in 1700 on analytical geometry of three dimensions. His works were collected and published in three volumes at Paris in 1713. Joseph Saurin, born at Courtaison in 1659, and died at Paris on Dec. 29, 1737, was the first to show how the tangents at the multiple points of curves could be determined by analysis. Jean Paul de Gua de Malves was born at Carcassonne in 1713, and died at Paris on June 2, 1785. He published in 1740 a work on analytical geometry in which he applied it, without the aid of the differential calculus, to find the tangents, asymptotes, and various singular points of an algebraical curve; and he further shewed how singular points and isolated loops were affected by conical projection. He gave the proof of Descartes's rule of signs which is to be found in most modern works. It is not clear whether Descartes ever proved it strictly, and Newton seems to have regarded it as obvious.
Gabriel Cramer, born at Geneva in 1704, and died at Bagnols
in 1752, was professor at Geneva. The work by which he is best
known is his treatise on algebraic curves published in 1750, which,
as far as it goes, is fairly complete; it contains the earliest
demonstration that a curve of the nth degree is in general
determined if
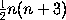 points on it be given. This work
is still sometimes read. Besides this, he edited the works of the
two elder Bernoullis; and wrote on the physical cause of the
spheroidal shape of the planets and the motion of their apses,
1730, and on Newton's treatment of cubic curves, 1746.
points on it be given. This work
is still sometimes read. Besides this, he edited the works of the
two elder Bernoullis; and wrote on the physical cause of the
spheroidal shape of the planets and the motion of their apses,
1730, and on Newton's treatment of cubic curves, 1746.
Jacopo Francesco, Count Riccati, born at Venice on May 28, 1676, and died at Trèves on April 15, 1754, did a great deal to disseminate a knowledge of the Newtonian philosophy in Italy. Besides the equation known by his name, certain cases of which he succeeded in integrating, he discussed the question of the possibility of lowering the order of a given differential equation. His works were published at Trèves in four volumes in 1758. He had two sons who wrote on several minor points connected with the integral calculus and differential equations: these were Vincenzo, who was born in 1707 and died in 1775, and Giordano, who was born in 1709 and died in 1790.
Giulio Carlo, Count Fagnano, and Marquis de Toschi, born at Sinigaglia on Dec. 6, 1682, and died on Sept. 26, 1766, may be said to have been the first writer who directed attention to the theory of elliptic functions. Failing to rectify the ellipse or hyperbola, Fagnano attempted to determine arcs whose difference should be rectifiable. He also pointed out the remarkable analogy existing between the integrals which represent the arc of a circle and the arc of a lemniscate. Finally he proved the formula
where i stands for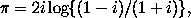
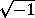 .
His works were collected
and published in two volumes at Pesaro in 1750.
.
His works were collected
and published in two volumes at Pesaro in 1750.
It was inevitable that some mathematicians should object to methods of analysis founded on the infinitesimal calculus. The most prominent of these were Viviani, De la Hire, and Rolle, whose names were mentioned at the close of chapter XV.
This page is included in a collection of mathematical biographies taken from A Short Account of the History of Mathematics by W. W. Rouse Ball (4th Edition, 1908).
Transcribed by