British Contemporaries of Newton, Taylor, Maclaurin and Simpson
From `A Short Account of the History of Mathematics' (4th edition, 1908)
by W. W. Rouse Ball.
David Gregory |
Halley |
Ditton |
Cotes |
Demoivre |
Stewart
It was almost a matter of course that the English
should at first have adopted the notation of Newton in the
infinitesimal calculus in preference to that of Leibnitz and
consequently the English school would in any case have developed
on somewhat different lines to that on the continent, where a
knowledge of the infinitesimal calculus was derived solely from
Leibnitz and the Bernoullis. But this separation into two distinct
schools became very marked owing to the action of Leibnitz and John
Bernoulli, which was naturally resented by Newton's friends; and
so for forty or fifty years, to the disadvantage of both sides,
the quarrel raged. The leading members of the English school were
Cotes, Demoivre, Ditton, David
Gregory, Halley, Maclaurin, Simpson,
and Taylor. I may, however, again remind my readers that
as we approach modern times the number of capable mathematicians
in Britain, France, Germany and Italy becomes very considerable,
but that in a popular sketch like this book it is only the leading
men whom I propose to mention.
To David Gregory, Halley and Ditton I need devote but few words.
David Gregory, the nephew of the James
Gregory mentioned above, born at Aberdeen on June 24, 1661, and
died at Maidenhead on Oct. 10, 1708, was appointed professor at
Edinburgh in 1684, and in 1691 was on Newton's recommendation
elected Savilian professor at Oxford. His chief works are one on
geometry, issued in 1684; one on optics, published in 1695, which
contains [p. 98] the earliest suggestion of the possibility of
making an achromatic combinations of lenses; and one on the Newtonian
geometry, physics, and astronomy, issued in 1702.
Edmund Halley, born in London in 1656, and died at Greenwich
in 1742, was educated at St. Paul's School, London, and Queen's
College, Oxford, in 1703 succeeded Wallis as Savilian professor,
and subsequently in 1720 was appointed astronomer-royal in succession
to Flamsteed, whose Historia Coelestis Britannica he
edited; the first and imperfect edition was issued in 1712. Halley's
name will be recollected for the generous manner in which he secured
the immediate publication of Newton's Principia in
1687. Most of his original work was on astronomy and allied
subjects, and lies outside the limits of this book; it may be,
however, said that the work is of excellent quality, and both
Lalande and Mairan speak of it in the highest terms. Halley
conjecturally restored the eighth and lost book of the conics of
Apollonius, and in 1710 brought out a magnificent edition of the
whole work; he also edited the works of Serenus, those of Menelaus, and
some of the minor works of Apollonius. He was in his turn succeeded at
Greenwich as astronomer-royal by Bradley.
Humphry Ditton was born at Salisbury on May 29, 1675, and
died in London in 1715 at Christ's Hospital, where he was mathematical
master. He does not seem to have paid much attention to mathematics
until he came to London about 1705, and his early death was a
distinct loss to English science. He published in 1706 a text book
on fluxions; this and another similar work by William Jones, which
was issued in 1711, occupied in England much the same place as
l'Hospital's treatise did in France. In 1709 Ditton issued an
algebra, and in 1712 a treatise on perspective. He also wrote
numerous papers in the Philosophical Transactions.
He was the earliest writer to attempt to explain the phenomenon of
capillarity on mathematical principles; and he invented a method
for finding the longditude, which has been since used on various
occasions.
Roger Cotes was born near Leicester on July 10, 1682, and
died at Cambridge on June 5, 1716. He was educated at Trinity
College, Cambridge, of which society he was a fellow, and in 1706
was elected to the newly-created Plumian chair of astronomy in the
university of Cambridge. From 1709 to 1713 his time was mainly
occupied in editing the second edition of the Principia.
The remark of Newton that if only Cotes had lived ``we might have
known something'' indicates the opinion of his abilities held by
most of his contemporaries.
Cotes's writings were collected and published in 1722 under the
titles Harmonia Mensurarum and Opera
Miscellanea. His lectures on hydrostatics were published
in 1738. A large part of the Harmonia Mensurarum is
given up to the decomposition and integration of rational algebraical
expressions. That part which deals with the theory of partial
fractions was left unfinished, but was completed by Demoivre.
Cotes's theorem in trigonometry, which depends on forming the
quadratic factors of
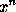 - 1, is well known. The proposition
that ``if from a fixed point O a line be drawn cutting a
curve in
- 1, is well known. The proposition
that ``if from a fixed point O a line be drawn cutting a
curve in
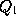 ,
,
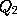 ,...,
,...,
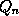 ,
and a point P be taken on
the line so that the reciprocal of OP is the arithmetic mean
of the reciprocals of
,
and a point P be taken on
the line so that the reciprocal of OP is the arithmetic mean
of the reciprocals of
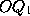 ,
,
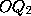 ,...,
,...,
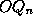 ,
then the locus of
P will be a straight line'' is also due to Cotes. The title
of the book was derived from the latter theorem. The Opera
Miscellanea contains a paper on the method for determining
the most probable result from a number of observations. This was
the earliest attempt to frame a theory of errors. It also contains
essays on Newton's Methodus Differentialis, on the
construction of tables by the method of differences, on the descent
of a body under gravity, on the cycloidal pendulum, and on projectiles.
,
then the locus of
P will be a straight line'' is also due to Cotes. The title
of the book was derived from the latter theorem. The Opera
Miscellanea contains a paper on the method for determining
the most probable result from a number of observations. This was
the earliest attempt to frame a theory of errors. It also contains
essays on Newton's Methodus Differentialis, on the
construction of tables by the method of differences, on the descent
of a body under gravity, on the cycloidal pendulum, and on projectiles.
Abraham Demoivre (more correctly written
as de Moivre) was born at Vitry on May 26, 1667, and died
in London on November 27, 1754. His parents came to England when
he was a boy, and his education and friends were alike English.
His interest in the higher mathematics is said to have originated
in his coming by chance across a copy of Newton's Principia.
From the éloge on him delivered in 1754 before the
French Academy it would seem that his work as a teacher of mathematics
had led him to the house of the Earl of Devonshire at the instant
when Newton, who had asked permission to present a copy of his work
to the earl, was coming out. Taking up the book, and charmed by
the far-reaching conclusions and the apparent simplicity of the
reasoning, Demoivre thought nothing would be easier than to master
the subject, but to his surprise found that to follow the argument
overtaxed his powers. He, however, bought a copy, and as he had
but little leisure he tore out the pages in order to carry one or
two of them loose in his pocket so that he could study them in the
intervals of his work as a teacher. Subsequently he joined the
Royal Society, and became intimately connected with Newton, Halley,
and other mathematicians of the English school. The manner of his
death has a certain interest for psychologists. Shortly before it
he declared that it was necessary for him to sleep some ten minutes
or a quarter of an hour longer each day than the preceding one.
The day after he had thus reached a total of something over
twenty-three hours he slept up to the limit of twenty-four hours,
and then died in his sleep.
He is best known for having, together with Lambert, created that
part of trigonometry which deals with imaginary quantities. Two
theorems on this part of the subject are still connected with his
name, namely, that which asserts that
sin nx + i cos nx
is one
of the values of
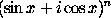 ,
and that which gives the
various quadratic factors of
,
and that which gives the
various quadratic factors of
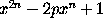 .
His chief
works, other than numerous papers in the Philosophical
Transactions, were The Doctrine of Chances,
published in 1718, and the Miscellanea Analytica,
published in 1730. In the former the theory of recurring series
was first given, and the theory of partial fractions which Cotes's
premature death had left unfinished was completed, while the rule
for finding the probability of a compound event was enunciated.
The latter book, besides the trigonometrical propositions mentioned
above, contains some theorems in astronomy, but they are treated
as problems in analysis.
.
His chief
works, other than numerous papers in the Philosophical
Transactions, were The Doctrine of Chances,
published in 1718, and the Miscellanea Analytica,
published in 1730. In the former the theory of recurring series
was first given, and the theory of partial fractions which Cotes's
premature death had left unfinished was completed, while the rule
for finding the probability of a compound event was enunciated.
The latter book, besides the trigonometrical propositions mentioned
above, contains some theorems in astronomy, but they are treated
as problems in analysis.
Maclaurin was succeeded in his chair at Edinburgh by his pupil
Matthew Stewart, born at Rothesay in 1717 and died at
Edinburgh on January 23, 1785, a mathematician of considerable
power, to whom I allude in passing, for his theorems on the problem
of three bodies, and for his discussion, treated by transversals
and involution, of the properties of the circle and straight line.
This page is included in a
collection of mathematical biographies taken from
A Short Account of the History of Mathematics
by W. W. Rouse Ball (4th Edition, 1908).
Transcribed by
D.R. Wilkins
(dwilkins@maths.tcd.ie)
School of Mathematics
Trinity College, Dublin
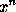 - 1, is well known. The proposition
that ``if from a fixed point O a line be drawn cutting a
curve in
- 1, is well known. The proposition
that ``if from a fixed point O a line be drawn cutting a
curve in
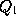 ,
,
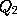 ,...,
,...,
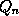 ,
and a point P be taken on
the line so that the reciprocal of OP is the arithmetic mean
of the reciprocals of
,
and a point P be taken on
the line so that the reciprocal of OP is the arithmetic mean
of the reciprocals of
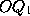 ,
,
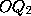 ,...,
,...,
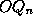 ,
then the locus of
P will be a straight line'' is also due to Cotes. The title
of the book was derived from the latter theorem. The Opera
Miscellanea contains a paper on the method for determining
the most probable result from a number of observations. This was
the earliest attempt to frame a theory of errors. It also contains
essays on Newton's Methodus Differentialis, on the
construction of tables by the method of differences, on the descent
of a body under gravity, on the cycloidal pendulum, and on projectiles.
,
then the locus of
P will be a straight line'' is also due to Cotes. The title
of the book was derived from the latter theorem. The Opera
Miscellanea contains a paper on the method for determining
the most probable result from a number of observations. This was
the earliest attempt to frame a theory of errors. It also contains
essays on Newton's Methodus Differentialis, on the
construction of tables by the method of differences, on the descent
of a body under gravity, on the cycloidal pendulum, and on projectiles.
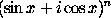 ,
and that which gives the
various quadratic factors of
,
and that which gives the
various quadratic factors of
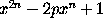 .
His chief
works, other than numerous papers in the Philosophical
Transactions, were The Doctrine of Chances,
published in 1718, and the Miscellanea Analytica,
published in 1730. In the former the theory of recurring series
was first given, and the theory of partial fractions which Cotes's
premature death had left unfinished was completed, while the rule
for finding the probability of a compound event was enunciated.
The latter book, besides the trigonometrical propositions mentioned
above, contains some theorems in astronomy, but they are treated
as problems in analysis.
.
His chief
works, other than numerous papers in the Philosophical
Transactions, were The Doctrine of Chances,
published in 1718, and the Miscellanea Analytica,
published in 1730. In the former the theory of recurring series
was first given, and the theory of partial fractions which Cotes's
premature death had left unfinished was completed, while the rule
for finding the probability of a compound event was enunciated.
The latter book, besides the trigonometrical propositions mentioned
above, contains some theorems in astronomy, but they are treated
as problems in analysis.