Electron. J. Diff. Equ.,
Vol. 2012 (2012), No. 91, pp. 1-10.
Positive almost periodic solutions for state-dependent
delay Lotka-Volterra competition systems
Yongkun Li, Chao Wang
Abstract:
In this article, using Mawhin's continuation theorem of coincidence
degree theory, we obtain sufficient conditions for the existence
of positive almost periodic solutions for the system of equations
![$$
\dot{u}_i(t)=u_i(t)\Big[r_i(t)-a_{ii}(t)u_i(t)
-\sum_{j=1, j\neq i}^na_{ij}(t)u_j\big(t-\tau_j(t,u_1(t),
\dots,u_n(t))\big)\Big],
$$](gifs/aa.gif)
where
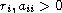 ,
,
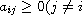 ,
,
 are
almost periodic functions,
are
almost periodic functions,
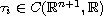 ,
and
,
and
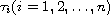 are almost periodic in
are almost periodic in
 uniformly for
uniformly for
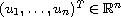 .
An example and its
simulation figure illustrate our results.
.
An example and its
simulation figure illustrate our results.
Submitted April 12, 2012. Published June 7, 2012.
Math Subject Classifications: 34K14, 92D25.
Key Words: Lotka-Volterra competition system; almost periodic solutions;
coincidence degree; state dependent delays.
Show me the PDF file (251 KB),
TEX file, and other files for this article.
 |
Yongkun Li
Department of Mathematics, Yunnan University
Kunming, Yunnan 650091, China
email: yklie@ynu.edu.cn
|
|---|
 |
Chao Wang
Department of Mathematics, Yunnan University
Kunming, Yunnan 650091, China
email: super2003050239@163.com
|
|---|
Return to the EJDE web page
![$$
\dot{u}_i(t)=u_i(t)\Big[r_i(t)-a_{ii}(t)u_i(t)
-\sum_{j=1, j\neq i}^na_{ij}(t)u_j\big(t-\tau_j(t,u_1(t),
\dots,u_n(t))\big)\Big],
$$](gifs/aa.gif)
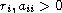 ,
,
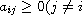 ,
,
 are
almost periodic functions,
are
almost periodic functions,
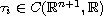 ,
and
,
and
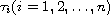 are almost periodic in
are almost periodic in
 uniformly for
uniformly for
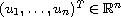 .
An example and its
simulation figure illustrate our results.
.
An example and its
simulation figure illustrate our results.

