In this paper, we consider the following dynamic system with parameter on a measure chain
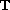 ,
,
![$$\displaylines{
u^{\Delta\Delta}_{i}(t)+\lambda h_{i}(t)f_{i}(u_{1}(\sigma(t)),
u_{2}(\sigma(t)),\dots ,u_{n}(\sigma(t)))=0,\quad
t\in[a,b], \cr
\alpha u_{i}(a)-\beta u^{\Delta}_{i}(a)=0,\quad
\gamma u_{i}(\sigma(b))+\delta u^{\Delta}_{i}(\sigma(b))=0,
}$$](gifs/ab.gif)
where
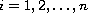 .
Using fixed-point index theory, we find
sufficient conditions the existence of positive solutions.
.
Using fixed-point index theory, we find
sufficient conditions the existence of positive solutions.
Shuang-Hong Ma, Jian-Ping Sun, Da-Bin Wang
Abstract:
In this paper, we consider the following dynamic system with
parameter on a measure chain
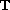 ,
,
![$$\displaylines{
u^{\Delta\Delta}_{i}(t)+\lambda h_{i}(t)f_{i}(u_{1}(\sigma(t)),
u_{2}(\sigma(t)),\dots ,u_{n}(\sigma(t)))=0,\quad
t\in[a,b], \cr
\alpha u_{i}(a)-\beta u^{\Delta}_{i}(a)=0,\quad
\gamma u_{i}(\sigma(b))+\delta u^{\Delta}_{i}(\sigma(b))=0,
}$$](gifs/ab.gif)
where
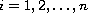 .
Using fixed-point index theory, we find
sufficient conditions the existence of positive solutions.
.
Using fixed-point index theory, we find
sufficient conditions the existence of positive solutions.
Submitted January 9, 2007. Published May 15, 2007.
Math Subject Classifications: 34B15, 39A10.
Key Words: Dynamic system; positive solution; cone; fixed point;
measure chain.
Show me the PDF file (212K), TEX file, and other files for this article.
| Shuang-Hong Ma Department of Applied Mathematics Lanzhou University of Technology Lanzhou, Gansu, 730050, China email: mashuanghong@lut.cn | |
 |
Jian-Ping Sun Department of Applied Mathematics Lanzhou University of Technology Lanzhou, Gansu, 730050, China email: jpsun@lut.cn |
 |
Da-Bin Wang Department of Applied Mathematics Lanzhou University of Technology Lanzhou, Gansu, 730050, China email: wangdb@lut.cn |
Return to the EJDE web page