 -point
boundary-value problems
-point
boundary-value problems
 -point
boundary-value problems
-point
boundary-value problems
Nickolai Kosmatov
Abstract:
We study the
 -point
nonlinear boundary-value problem
-point
nonlinear boundary-value problem
![$$
\displaylines{
-[p(t)u'(t)]' = \lambda f(t,u(t)), \quad 0 less than t less than 1, \cr
u'(0) = 0, \quad \sum_{i=1}^{m-2}\alpha_i u(\eta_i) = u(1),
}$$](gifs/ab.gif)
where
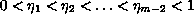 ,
,
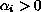 for
for
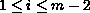 and
and
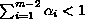 ,
,
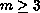 .
We assume that
.
We assume that
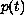 is non-increasing continuously differentiable
on
is non-increasing continuously differentiable
on
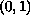 and
and
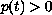 on
on
![$[0,1]$](gifs/ak.gif) .
Using a cone-theoretic approach we provide sufficient conditions
on continuous
.
Using a cone-theoretic approach we provide sufficient conditions
on continuous
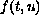 under which the problem admits a positive
solution.
under which the problem admits a positive
solution.
Submitted April 23, 2004. Published October 10, 2004.
Math Subject Classifications: 34B10, 34B18.
Key Words: Green's function; fixed point theorem;
positive solutions; multi-point boundary-value problem.
Show me the PDF file (204K), TEX file, and other files for this article.
| Nickolai Kosmatov Department of Mathematics and Statistics University of Arkansas at Little Rock Little Rock, AR 72204-1099, USA email: nxkosmatov@ualr.edu |
Return to the EJDE web page