A Generic Parallel Genetic Algorithm




by


Roderick Murphy (B.E.)


A Thesis submitted to

The University of Dublin

for the degree of


M.Sc. in High Performance Computing


Department of Mathematics

University of Dublin

Trinity College




October 2003









ABSTRACT


Genetic algorithms have been proven to be both an efficient and effective means of solving certain types of search and optimisation problems. This project provides a library of functions that enable a user to implement variations of commonly used genetic algorithm operators, including fitness function scaling, selection, crossover, mutation and migration, with which they can solve their specified problem. The main function is parallelised using Pthreads. Using the prisoners' dilemma as an example problem, results show a significant speed-up compared with a purely serial implementation.



ACKNOWLEDGEMENTS


Firstly I would like to thank Mr Dermot Frost for his guidance and introduction to this extremely interesting topic. I would also like to thank my HPC class for their pearls of wisdom and tips for using the many useful applications that made this project a reality. In particular I owe my gratitude to Paddy for the hours he spent helping me debug my code and find the numerous tpyeos in this thesis. Also Dave, Rachel, Madeleine and Brian for the numerous cups of coffee and helpful debate on a wide range of both useful and useless topics. Finally I would like to thank my family for their love and support throughout the year.

Contents


1.0. Introduction to Genetic Algorithms

1.1. Introduction

1.2. Search Spaces

1.3. A Simple Example

1.4. Comparison between Biological and GA Terminology

1.5. Applications of Genetic Algorithms

1.6. How or why do Genetic Algorithms work?


2.0. GA Operators in Further Depth

2.1. Introduction

2.2. Encoding a Problem

2.3.0. Selection

2.3.1 Fitness Proportional Selection

2.3.2 Rank Selection

2.3.3. Tournament Selection

2.4.0. Fitness Scaling

2.4.1. Linear Scaling

2.4.2. Sigma Truncation

2.3.3. Power Law Scaling

2.5. Elitism

2.6.0. Crossover

2.6.1. Single-point crossover

2.6.2. Multi-point crossover

2.6.3. Parameterized Uniform Crossover

2.7. Mutation

2.8. Inversion

2.9. Parameter Values for Genetic Algorithms

2.10. Conclusion


3.1. Introduction

3.2. Master Slave parallel GA prototype

3.3. Distributed, Asynchronous Concurrent parallel GA prototype

3.4. Network parallel GA

3.5. Island Model

3.5. Conclusion


4.1. Introduction

4.2. Objective Value function

4.3. Parallel Genetic Algorithm Function

4.4.0. Implementation of Migration Operators

4.4.1. What Technology Was Used?

4.4.2. Threaded Implementation

4.5. Conclusion

5.0. Results

5.1. Introduction

5.2.0. The Prisoners Dilemma using Parallel GA [MI96]

5.2.1. Encoding

5.2.2. Genetic Algorithm

5.2.3. Serial Implementation

5.2.4. Results

5.3. Conclusion


6.0. Conclusions and Future Directions

6.1. Introduction

6.2. Future Directions

6.3. Conclusion


References

1.0. Introduction to Genetic Algorithms



1.1. Introduction


Goldberg [GO89] describes Genetic Algorithms as: search procedures based on the mechanics of natural selection and natural genetics. I.e. they are general search and optimisation algorithms that use the theories of evolution as a tool to solve problems in science and engineering. This involves evolving a population of candidate solutions to the particular problem, using operations inspired by natural genetic variation and natural selection.


Genetic Algorithms are 'weak' optimisation methods. That is they do not use domain-specific knowledge in their search procedure. For this reason they can be used to solve a wide range of problems. The disadvantage, of course, is that they may not perform as well as algorithms designed specifically to solve a given problem.


From the very beginning, computer scientists have thought of systems that would mimic one or more attributes of life. However, it wasn't until the 1960s that Genetic Algorithms (GAs) were formally developed by John Holland, along with his students and colleagues from the University of Michigan. Holland’s original goal, however, was not to design algorithms to solve specific problems, as in other evolutionary programming, but to study the phenomenon of adaptation as it occurs in nature and to develop ways in which the mechanisms of natural adaptation might be imported into computer systems.


Holland's GA is a method of moving from one population of chromosomes (strings of ones and zeros) to a new population using a kind of natural selection, together with the genetics-inspired operations of crossover, mutation and inversion.

A typical algorithm might consist of the following:



With these being the basic components of most GAs it can be seen that they are a simple method to solve a specific problem. The downside, however, is that there are many different ways of performing these steps. In this dissertation I have attempted to provide a package that gives the user a choice of using some of the more common methods to solve their particular problem.


Note that Holland's inversion operation is rarely used in GAs today since its benefits, if any, are not well established.

1.2. Search Spaces


For many search or optimisation problems in science, engineering and elsewhere, there are a huge or even infinite number of possible solutions. This means that in most cases it is impossible to check each and every possible solution in order to find the optimum or required one. One approach is to limit the number of possibilities to within a chosen range with a certain step size or distance between each one. This method is used in all problems solved using a computer, since after all there is a limit to the granularity at which a digital computer can represent a problem. The set of possible solutions is called a 'search space'.

Associated with the idea of a search space is the concept of a 'fitness landscape' (defined by the biologist Sewell Wright in 1931). The fitness landscape is a measure of the success, or fitness, of each solution within the search space. It is this fitness that is used to determine which solutions of the GA population go forward to produce the new solutions.


These landscapes can have surprisingly complex topographies. For a simple problem of two variables (adjustable parameters), the fitness landscape can be viewed as a three-dimensional plot showing the variation of the fitness for varying input parameters. This plot can have a number of peaks (maxima) and troughs (minima). The highest peak is usually referred to as the global maximum or global optimum. The lesser peaks are referred to as local maxima or local optima. For many search problems the goal is to find the global optimum. However, there are situations where for example any point above a certain threshold will suffice. In other problems for example in aesthetic design, a large number of highly fit yet distant, and therefore distinct, solutions might be required.


There is one caveat with the notion of fitness landscape with respect to GAs. Just as in the natural world, the fitness of any organism depends on the other organisms around it and not just on its surroundings alone. This means that the fitness landscape of many types of GAs is in a constant state of change.


In general GAs attempt to find the highest peak in the fitness landscape of a given problem. They do this using a combination of exploitation and exploration. That is, when the algorithm has found a number of good candidate solutions it exploits them by combining different parts of each solution to form new candidate solutions. This process is known as crossover. GAs also explore the fitness landscape through the creation of new candidate solutions by randomly changing parts of old solutions. This process is known as mutation.



1.3. A Simple Example


In order to clarify how GAs work I will present a simple example [from MI96]. Firstly given a specific problem we must choose a means of encoding each solution. The most common approach is to represent each solution as a binary string of length l bits.

We start by randomly generating n such strings. These are the candidate solutions to the problem.


By decoding each string to some value x, calculate its fitness, f(x).Repeat the following steps until n offspring (new population members) have been created.



Replace the old population with the n offspring. Calculate the fitness of the new members and start the process again.


Each iteration of this process is called a generation. Fifty to 100 generations are typically carried out to solve a problem using a GA and the entire set of generations is called a run. The fittest member over the entire run is typically taken as the required solution.


The are a number of details to be filled in with regard to each step of the algorithm as well as the values such as the number of members in the population and the probabilities of crossover and mutation. These details will be dealt with in the next chapter.



1.4. Comparison between Biological and GA Terminology


Not surprisingly much of the language used by the GA community has its origins in that used by biologists. Some of the analogies are somewhat strained, since GAs are generally greatly simplified compared with the real world genetic processes.


All living organisms consist of cells with each cell containing the same set of one or more chromosomes, or strings of DNA that serve as a 'blueprint' for that individual organism. The binary (or other) string used in the GAs described above can be considered to be a chromosome, but since only individuals with a single string are considered in most GAs, the chromosome is also the genotype (The genotype is the name given to the total number of chromosomes of an organism, for example, the human genotype is comprised of 23 pairs of chromosomes).


Each chromosome can be subdivided into genes, each of which, roughly speaking, encode a particular trait in the organism (e.g. eye colour). Each of the possible values a gene can take on is called an allele (e.g. blue, green, brown or hazel). The position of a gene in the chromosome is called its locus.


In GA terminology, if we consider a multi-variable problem, a gene can be considered as the bits that encode a particular parameter and an allele, an allowable value that parameter can have.


The organism or phenotype is the result produced by the expression of the genotype within its environment. In GAs this will be a particular set of unknown parameters, or an individual solution vector.


Organisms, such as humans, whose chromosomes are arranged in pairs, are called diploid. Organisms whose chromosomes are unpaired are called haploid. Most sexually reproducing species are diploid, however, for simplicity most GAs only consider unpaired chromosomes.


In nature mutation occurs when single nucleotides (elementary molecules of DNA) get changed when being copied from parent to offspring. In GAs mutation consists of flipping binary digits at a randomly chosen locus in the chromosome.



1.5. Applications of Genetic Algorithms


The lists of fields and types of problems to which genetic algorithms have been successfully applied are ever growing. The following are just a few examples:


Optimisation tasks: including numerical optimisation and such combinatorial optimisation tasks such as circuit layout and job scheduling.


Automatic Programming: they have been used to evolve computer programs for specific tasks, and to design other computational structures such as automata and sorting networks.


Machine learning: GAs have been used for operations such as classification and prediction tasks in weather forecasting or protein structure. They have also been used to evolve aspects of particular machine learning systems such as weights for neural networks, rules for learning classifier systems or symbolic production systems and sensors for robots.


Economics: they have been used to model processes of innovation, the development of bidding strategies, and the emergence of economic markets.


Immune systems: they have been used to model aspects of natural immune systems.


Ecology: GAs have been used to model biological arms races, host-parasite co-evolution, symbiosis and resource flow.


Population genetics: This was Holland’s original reason for the development of GAs. It has been used to study questions such as 'Under what conditions will a gene be evolutionarily viable for recombination?'


Social systems: GAs have been used to study the evolutionary behaviour of social systems, such as that in insect colonies and more generally the evolution of co-operation and communication in multi-agent systems.


The above list gives a flavour of the kind of problems GAs are being used to solve, but it does not conclusively answer the question of the type of problems they should be used to solve.


It was previously stated that the GA is a 'search' tool, but what exactly does 'search' mean? Melanie Mitchell [MI96] describes three concepts for the meaning of the word search:


Search for stored data. This is the traditionally adopted meaning of a search. It involves searching a large database of records for some piece of data, like looking for a phone number and address in a phone book.


Search for paths to goals. The objective here is to efficiently find a set of actions that move a system from some initial state to some end goal. An example of this type of search is the 'Travelling salesman problem' where the goal is to find the shortest round trip between N cities, visiting each city only once.


Search for solutions. This is a more general class of search than search for paths to goals. This method involves efficiently finding the solution to a problem from a very large set of candidate solutions. It is this type of search method for which GAs are most commonly used.


However, even if a particular problem falls into the third category, this doesn't guarantee that a GA will be an efficient search algorithm. Unfortunately there is no rigorous answer as to exactly what kind of problems GAs can solve efficiently. There are, however, a few guidelines that researchers have found to hold true. The efficiency of a GA is related to the search space of the particular problem. Generally, a GA will perform well in problems that have large search spaces whose landscapes are not smooth or unimodal (i.e., consisting of a single smooth hill). That is that the search spaces are not well understood or are noisy. GAs also perform well in cases where it is more important to find a good solution rather than the absolute optimal solution.


Obviously if the search space is not large all solutions can be searched exhaustively and the best one can be found, whereas a GA might converge on a local optimum rather than the global optimum. If the search space is smooth or unimodal then a gradient ascent algorithm, such as steepest ascent hill climbing will, be more efficient than a GA. If the problem is well understood then search methods that use domain-specific information can be designed to outperform any general-purpose method such as a GA. Some search methods as in simple hill climbing might be lead astray in the presence of noise, but because GAs work by accumulating fitness statistics over many generations they will perform well in the presence of a small amount of noise.


However, taking the above into account the method with which the candidate solutions are encoded can predominantly dictate the performance of the GA.



1.6. How or why do Genetic Algorithms work?


There is no absolutely conclusive explanation as to why GAs do or even should work so effectively as search algorithms. There are, however, a number of theories, the most widely accepted (at least until recently) is the schemata theory introduced by Holland [HO75] and popularised by Goldberg [GO89].


The theory of schemas (or schemata) is based on the idea that GAs work by discovering, emphasising, and recombining good 'building blocks' of solutions. That is that good solutions tend to be comprised of good combinations of bit values that confer higher fitness on the strings in which they are present.


So a schema is a set of bit strings that can be described as a template made up of ones, zeros and asterisks, where asterisks represent 'don't care' values. E.g. the schema:


H = 1 * * * * 1


represents the set of all 6-bit strings that begin and end with 1. The strings 100101 and 101011 are called instances of the schema H.


We can estimate the fitness of a certain schema as the average fitness of all instances of that schema present in the population at any time, t (average fitness = û(H,t)). Thus we can calculate the approximate increase or decrease of any given schema over successive generations. A schema whose fitness is above average will produce an exponentially increasing number of samples. See [MI96] pp27-30 for a more in depth analysis.

2.0. GA Operators in Further Depth



2.1. Introduction


Having explained the basic mechanisms of genetic algorithms in the previous chapter, in this chapter I will attempt to explain some of the subtler details of some GA operators and also delve into the implementation of these functions.



2.2. Encoding a Problem


Perhaps the most important aspect for any GA to be successful is the manner in which the candidate solutions are encoded. Although unnatural, Holland and his students concentrated on binary encoding and much of the GA world has followed suit. Thus most of the theory has been developed around this type of encoding (although much of it can be extended to non-binary approaches), also the heuristic parameter settings, such as crossover and mutation rates, have been developed for GAs using binary encoding.


The problem with binary-valued encoding arises when the range of real world (phenotype) values are not a power of 2, some sort of clipping or scaling is required so that all binary gene or chromosome combinations represent some real world value.


The most frequently used method of binary encoding is standard binary coding (000 = 0, 001 = 1, 101 = 5 etc). An alternative method, however, is Gray coding. This is similar to binary encoding except that each successive number only differs by one bit. This has the advantage that single bit changes during mutation have less of an effect on the fitness of the string. Its disadvantage is that it slows exploration, the process of creating new solutions that are not made from parts of other solutions.


A more natural form of encoding is to use multi-character or real valued alphabets to form the chromosomes. Under Holland's schema theory, however, multi character encoded strings should perform worse than those encoded in binary. However, this has been shown not to be true. It seems the performance depends on the problem and the details of the GA – this poses a dilemma since, in general, GAs are used to solve problems about which not enough is known to solve them in other ways thus, the type of encoding that will work best cannot be known. One way around this is to use the same encoding that was used for a similar problem.


Another method is tree encoding [MI96 pp 35-44]. This allows search spaces to be open-ended since there is no limit to the size of the tree. However, this can also lead to pitfalls - the trees can grow too large and become uncontrolled, preventing the formation of more structured candidate solutions.


[MI96] proposes having the encoding adapt itself so that the GA finds the optimum method. This also solves the problem of fixed-length encoding limiting the complexity of the candidate solutions.

2.3.0. Selection

Selection is the operation whereby candidate solutions (chromosomes) are selected for reproduction. In general the probability of selection should be proportional to the fitness of the chromosome in question. To make this possible we must make the following assumptions: firstly, there must be some measurable quality in order to solve the problem - the fitness, secondly, that the solution can be found by maximising the fitness, and lastly, that all fitness values, both good and bad, should be positive. With these conditions satisfied there are a number of different ways in which we can select members from the population for crossover. The most common of these is fitness proportionate selection.





2.3.1. Fitness Proportionate Selection



If fi is the fitness of individual i and is the average population fitness, where N is the population size, then the probability of an individual i being selected for crossover is:








This can be implemented using the roulette wheel algorithm. As the name suggests a wheel is constructed with a marker for each member in the population, the size of each marker being proportional to that individual's fitness. Thus as the wheel is spun the probability of the roulette landing on the marker for individual i is pi.



This algorithm can be simulated using the cumulative distribution representation - A random number, r, is generated between zero and the sum of each individual's fitness value. The first population member whose fitness, added to the fitness of the preceding members, is greater than or equal to r is returned.


There are, however, problems with this method of selection under certain conditions. Consider the case when a certain individual's fitness is very much greater that the average population fitness. Under fitness proportionate selection this member will be chosen much more frequently than other members in the population. Thus, over a few generations the gene pool will become saturated with its genes. If this member's phenotype resides close to a local maximum, and not the global maximum, in the fitness landscape then the GA, without the help of mutation or even hyper-mutation (mutation with a very high mutation rate - discussed later), can become stuck at this local maximum. This is known as premature convergence.


Another problem with fitness proportionate selection is that of stagnation. This generally occurs towards the end of a run, although it can happen at any time. If all individuals have similar fitnesses, then fitness proportionate selection will impose less selection pressure and so will be almost as likely to pick the fittest members as the least fit members.



Both these problems can be solved using fitness scaling techniques, which will be discussed in §2.4. However, there are different selection methods available that do not suffer from the above problems.





2.3.2. Rank Selection



In this selection operation all individuals are sorted by increasing values of fitness. Each individual is then assigned a probability, pi, of being selected from some prior probability distribution. Typical distributions include:



Linear: pi = a i + b, (a < 0)

and

Negative exponential: pi = a e(b i + c)



Fig 2.1 Plot of linear and negative exponential distributions used for rank selection.



The values of a and b are calculated by satisfying the following conditions:





These result in the following equations:









where N is the population size. By choosing an appropriate value for c we can dictate how selection is carried out. Generally c is taken as ~ 2.



Rank selection solves the problem of premature convergence and stagnation and the size of the gaps between fitnesses become irrelevant. However, there is little evidence of this selection method occurring in nature, making its use difficult to justify. The reordering process also introduces a computational overhead making it less engaging.





2.3.3. Tournament Selection



This can be viewed as a noisy version of rank selection. The selection process is thus: select a group of N (N < 1) members, then select the fittest member of this group and discard the rest.



Tournament selection inherits the advantages of rank selection but does not require the global reordering of the population and is more inspired by nature.





2.4.0. Fitness Scaling



The two undesirable characteristics of fitness proportionate selection, premature convergence and stagnation, can cause problems with the selection procedure. Rather than choosing an alternative selection method, one can choose to scale the fitness values so as to reduce these unwanted effects, while still using fitness proportionate selection methods such as roulette wheel selection. There are three main types of scaling used by the GA community.





2.4.1. Linear Scaling


The fitness of each individual, f, is replaced by f ' = a.f + b

where a and b are chosen so that:


1. The scaled average fitness is equal to the raw average fitness ().

2. The maximum value of the scaled fitness is some constant times the average fitness. This constant, c, is the number of expected copies desired for the best individual (usually c = 2).


These conditions result in the following equations for a and b:




One problem with linear scaling, particularly if is close to fmax or if a given fitness is very much less than , is that fitness values can become negative. To solve this we can set any negative fitness values to zero. This, however, is obviously undesirable since this means that these individuals will never be selected. Another way to solve this problem is to use an alternative scaling method such as sigma truncation.



2.4.2. Sigma Truncation


With sigma truncation, f is replaced by f ' = f - ( - c. sigma ). Where sigma is the population standard deviation, c, is a reasonable multiple of (Usually 1 <= c <= 3). Sigma truncation removes the problem of scaling to negative values. Truncated fitness values can also be scaled if desired.



2.4.3. Power Law Scaling


With power law scaling f is replaced by for some suitable power k. This method is not used very often since in general, k is problem-dependent and may require dynamic change to stretch or shrink the range as needed.



Even when using the above methods of selection and scaling there is a chance that the individual representing the correct solution might not get picked. To prevent this the best individuals can be placed in a temporary buffer before selection and then added into the new population after selection, crossover and mutation have been carried out. The process of keeping these elite individuals is known as elitism.



2.6.0. Crossover


Once parents have been selected their genes must be combined in some way to produce offspring. In genetics this process is called crossover. The crossover operator exchanges subparts (genes) of two chromosomes, roughly mimicking recombination between two haploid (single chromosome) organisms. There are a number of ways of which to exchange these genes, most, however, involve using variations of either single-point crossover or multi-point crossover.



This is the simplest form of crossover in which a single crossover point is chosen between two loci in the chromosomes of two population individuals. The bits up to this point in the first individual then get swapped with the corresponding bits from the second individual, to form two new chromosomes. The crossover point can either be pre-selected or chosen randomly.


When the crossover point is fixed throughout the run, however, it may be difficult for the GA to find the optimum solution since, barring mutation, new gene combinations at one or both ends of the chromosome can not be created.



2.6.2. Multi-point crossover


In this form of crossover, a number of crossover points are chosen (again either before-hand or randomly). The bits between every second grouping of bits (i.e. bits between every second crossover point) are swapped between two individuals to produce the offspring.



Multi-point crossover can also be susceptible to the same problems as the simpler single point case, albeit to a much lesser degree. To solve this problem we again turn to nature. In nature the copying of genetic material from parents to offspring is not a perfect process. Often errors are made. Most organisms, however, are able to correct many of these copying mistakes themselves. But not all mistakes are corrected these are called mutations. It turns out that these uncorrected copying errors can actually be beneficial and can help a species adapt to different environments.





2.6.3. Parameterised Uniform Crossover



A variation on multi-point crossover is parameterised uniform crossover. This method randomly chooses whether or not alleles are to be swapped at each locus. The probability of swapping a gene is typically set to between 0.5 and 0.8.



Parameterised uniform crossover, however, has no positional bias. This means that any schemas contained at different positions in the parents can potentially be recombined in the offspring.





2.7. Mutation



As in crossover, the mutation operator also has the effect of creating new population members. It can help create chromosomes that would not otherwise be formed by selection and crossover alone. In this way, mutation can allow the GA explore more of the fitness landscape and keep it from getting trapped in local optimal solutions.

Unlike natural genetics, generally, GAs do not make and then correct errors in the crossover operation, but instead randomly pick and change a small number of bits in an individual's chromosome.



Like many of the GA operations, the success of mutation lies in knowing when and how often to use it. Overuse of mutation can lead to populations not having sufficient chance to improve at all. Thus, there is generally a low probability of mutation associated with most GAs. In literature this is usually the probability of mutating each bit in the string and so is normally very small (~ 0.001).



Sometimes, especially late into the GA run, populations can stagnate and become stuck around local optima. When this happens, the gene pool can become too concentrated and standard mutation rates cannot generate sufficient diversity to enable the algorithm to free itself quickly enough. To overcome this, the mutation rate is raised to an augmented level for a generation or two. This process is called hyper-mutation.





2.8. Inversion



In his original research, Holland used a fourth operator called inversion. This involved occasionally reversing the order of part (or all of) an individual’s chromosome. Although, a similar operation occurs in nature, there has been little, if any, evidence of its benefit in genetic algorithms. This may be because, as they stand, most GAs rely heavily on the position and orientation of genes in the chromosome, whereas in nature, the position and orientation of genes are of less importance in the resulting phenotype. Thus, inversion has not been used in this project.





2.9. Parameter Values for Genetic Algorithms



As stated before, one of the key elements for the success of GAs is the choice of the various parameter values - such as population size, crossover rate and mutation rate. These parameters typically interact with each other in a non-linear fashion and as a result cannot be optimised one at a time. They also seem to differ for different types of problems and so there are no conclusive results as to what values should be chosen. Typically people use values that have produced good results in previous, similar problems.





One interesting idea noted by Grefenstette [GR86], was to have these parameters for a particular genetic algorithm optimised by another GA - since of course, that is what GAs do!



On the other hand, many in the GA community would agree that many of these parameters should be varied over the course of the run. For example hyper-mutation is essentially a variation of the mutation probability at certain generations during the run.





2.10. Conclusion



This chapter has dealt in detail with the various GA operators and options. There is still one more operator to be discussed - one that freely lends itself to parallelization - migration.


3.1. Introduction


In general the types of problems that are solved using algorithms such as GAs are slow to solve even on the fastest machines today. This is mainly due to a vast number of possible solutions combined with objective evaluation functions (i.e. functions that, given a certain trial input will produce the output) that are also relatively laborious. Algorithms such as simulated annealing or GAs attempt to find an optimum solution without having to explore all possible solutions.


In many of these problems these fitness evaluations for each candidate solution can be calculated independently. This means that each candidate solution can be calculated at the same time, in other words in parallel.


Performing these evaluations in parallel will obviously result in an increase in speed of the algorithm - roughly proportional to the number of processors used. There are, however, reasons for performing GAs in parallel that are believed to give improved performance. If we consider the GA as simply a model of natural systems then some parallel implementations can be viewed as consisting of separate sub-populations evolving independently of each other, with occasional migration allowed between these sub-populations.


As with other GA operators there is no 'correct' method (or even one known to be optimum) for parallelising a GA (although some methods may better suit certain types of problems than others). A number of implementations have been considered in [GR89], [GO89] and [CO99]:



DrawObject


The master slave implementation, outlined in figure 3.1, has a single master process and a number of slave processes. The master process controls selection, crossover and mutation while the slaves simply perform the function evaluations.


This is an example of a parallel GA implementation that does not mimic any migratory processes seen in nature; it only serves to speed up the algorithm.


Although straightforward and relatively easily to implement, this scheme suffers from two major drawbacks. Firstly, even on a machine whose architecture is homogeneous, if the time taken for one process to complete its function evaluations is less than that of the other processes, then the time difference is wasted waiting for the other processes to catch up before the next generation. Secondly, the algorithm relies on the health of the master process. If it fails then the system halts.


Having a sort of semi-synchronous master slave implementation can solve this first weakness. In this scheme the master process selects members on the fly as the slaves complete their work.




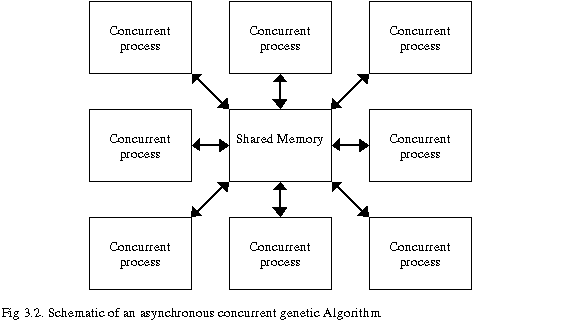
In this scheme k identical processors perform both genetic operators and function evaluations independently of each other. Each processor accesses a shared memory. The shared memory requires that no processor simultaneously hits the same memory location.


The asynchronous, concurrent scheme is slightly more difficult to implement than the previous implementation, however, reliability is improved.


There are problems, such as those in game theory and elsewhere, in which the fitness of a solution depends on the other candidate solutions. Obviously these can also be calculated in parallel, however, the processor used must have all candidate solutions stored in memory. This means that on a distributed memory machine overheads of sending and receiving solutions are greater. For fast generation evaluation these overheads may outweigh any benefits gained from parallel implementation.


3.4. Network parallel GA



The network parallel GA scheme is more closely related to the notion of migration in nature (although still a little unrealistic). In this method k independent sub-populations are evolved independently of each other. After each generation the fittest member from each sub-GA or island is broadcast to each other island, with a certain probability, pmig, Since communication is relatively intermittent the bandwidth required is less than with other methods. The reliability of this scheme is also greater than some of the others due to the autonomy of each sub-population.



3.5. Island Model



The island model, proposed by Goldberg [GO89], is probably most closely related to the notion of migration in nature. Unlike the network scheme, the island model introduces the idea of distance between sub-populations and by the same token a probability of migration between one island and another.


As can be seen in figure 3.4 there are different probabilities of going from island 'a' to island 'b' as there is of going from island 'b' to 'a'. This allows maximum flexibility for the migration process. It also mirrors the naturally inspired quality that, although two populations have the same separation no matter what way you look at them, it may be easier for one population to migrate to another than vice-versa. An example of this from nature could be the situation whereby it is easier for one species of fish to migrate down-stream than for a different species to migrate up-stream.


Note that there is no probability associated with the migration of an individual to or from the same island, since any migration would have the effect of creating a duplicate of the member selected for migration at the expense of the weakest member. This is in general undesirable, as it would reduce the variation in that islands gene pool.


These probabilities could be linked in with the average or maximum fitnesses of each island population. Migration could be set to occur only when a certain threshold has been met with regard to either of these measures. Alternatively the probability of migration in a particular island could be proportional to each individual's fitness.



3.5. Conclusion


It is easy to conceive many other, more elaborate, schemes to perform GAs in parallel or to model aspects of population migration. Although they might seem to be frivolous, there are important evolutionary theories underlying them. The next chapter will touch on how the migratory schemes, as well as some of the previous GA operators, were implemented in code.


4.1. Introduction


In the previous three chapters the fundamentals of genetic algorithms were introduced, the more commonly used operators were explored in depth and some parallel algorithms used to speed up genetic algorithms and to model aspects of migration were introduced. This chapter will explain how some of these more complicated functions were implemented in code and will then show how these migrationary implementations helped to speed up a sample problem solved using a GA.


The objective in writing this project was to write a small library of functions in C, with all functions culminating in a easily integrateable function which could implement a generic parallel genetic algorithm - ParallelGeneticAlgorithm(). The following is both a guide to using this function and an explanation as to how it was implemented in parallel.



4.2. Objective Value function


When using the function, ParallelGeneticAlgorithm(), the user would pass to it a pointer to a function which calculates the objective value of a given candidate solution. That is a means of comparing one candidate solution with another. This function, generally written by the user, should return the objective value as a positive double precision number. This works in the same way as the standard libc function qsort(), which accepts a pointer to a comparison function from the user. Using this function in conjunction with a number of other GA options and parameters, such as population size and crossover type, ParallelGeneticAlgorithm() would return the fittest individual from the entire run. All going to plan, this returned individual should be close to the required solution.


The objective value function had to have the following prototype:


double ObjectiveValueFunction(Population *pop,

int pop_size,

int individual,

int chromosome_length );


'pop' is a pointer to the structure 'Population', which has the following members:


typedef struct { Chromosome *genotype;

double obj_val;

double fitness;

GA_Status status;

int generation;

}Population;


Where: Chromosome is of type char (although this could be changed to suit different allele types).

genotype is a pointer to the chromosome binary (or otherwise) string.

obj_val is the value returned from the objective value function

fitness is the scaled objective value.

status is a status marker of type GA_Status for the individual.


GA_Status is integer-valued and can take on any of the following values:

GA_STATUS_ERROR

GA_STATUS_INVALID

GA_STATUS_OK

GA_STATUS_SELECTED

GA_STATUS_SORTED

GA_STATUS_ELITE


From the point of view of the user the only part of the population structure that they need be concerned about, in terms of their objective value function, is the Chromosome string genotype. All other members are handled inside the ParallelGeneticAlgorithm() function.


The user's objective value function must then take each individulas chromosome string, decode it into whatever variable (or variables) it represents and carry out the required evaluation on these variables and return some value representing the 'goodness' of that particular solution. The better the chromosome the bigger this value should be.


The following function, whose prototype is included in the header file ga.h may be of some use in writing the objective value function:


double DecodeGenotype( Chromosome *gene, int string_length,

double lower,

double upper );


This function takes the binary gene string gene of length string_length and converts it to a double precision number between the values lower and upper. Thus it can be used to convert certain genes in the chromosome string to their phenotypic values.


For integer valued phenotypes the function:


int String2Integer(char *string, int string_length);


can be used. Note that if two to power of the number of bits per gene (i.e. the number of possible values that gene can take) is greater than the number of values it is required to represent, then some sort of scaling in required so that each possible value of the gene string has some corresponding integer value.



4.3. Parallel Genetic Algorithm Function


Having written a function to evaluate the objective value, the user must then decide the types and arguments of scaling, selection, crossover, mutation and migration they want to use for the GA. As explained before, these choices are very much problem specific. In general most options will work for most types of problems, however, the best values can either be found by trial and error or by using values close to those used in similar problems.


Alternatively, once an objective function has been written, the GA function itself can be used to discover optimum option values for that specific problem [GR86].

These options are all passed to the function, as follows:


Population ParallelGeneticAlgorithm(int nislands, int ngenerations,

int nmembers, int string_length, GA_Op select_type, double select_arg,

int nelite, GA_Op cross_type, double cross_prob, int ncross_points,

int *gene_lengths, double mut_prob, GA_Op scaling_type,

double scale_arg, GA_Op mig_type, double *mig_prob,

double (*ObjectiveValueFunction)(Population *, int, int, int)

);


The arguments are as follows: (GA_Op is simply integer valued).


nislands The number of population islands to be created by the function.

ngenerations The number of generations to carry out.

nmembers The number of individuals on each island.

string_length The required length of each chromosome.

nelite The number of elite individuals per island per generation.

select_type The type of selection to be used.

The options are:

GA_SELECT_RAND Random selection

GA_SELECT_ROULETTE_WHEEL Roulette wheel selection

GA_SELECT_RANK_LINEAR Linear rank selection

GA_SELECT_RANK_NEG_EXP Negative exponential rank selection

GA_SELECT_TOURNAMENT Tournament selection


select_arg Argument used in the last three selection types as described in §2.3.2. and §2.3.3.

scaling_type The scaling type to be used.

Allowable options are:

GA_SCALE_NONE No scaling.

GA_SCALE_SIGMA_TRUNCATION Sigma Truncation.

GA_SCALE_LINEAR Linear scaling.

GA_SCALE_POWER_LAW Power law scaling.

scale_arg Argument used for the last two scaling arguments as described in §2.4.1. and §2.4.3.


cross_type The crossover type to be used.

Options that can be used are:

GA_CROSS_SINGLE Single point crossover.

GA_CROSS_MULTI Multi point crossover.

GA_CROSS_RANDOM Multi point random crossover.

GA_CROSS_RANDOM_SINGLE Single point random crossover.


cross_prob Probability of crossover.

ncross_points Number of crossover points (for multi point crossover).

gene_lengths A pointer to an array of gene lengths (of size one for single point crossover).

mut_prob Mutation rate.

mig_type Migration type.


Options are:

GA_MIG_NONE No migration.

GA_MIG_ISLAND Island migration model.

GA_MIG_NETWORK Network migration model.

mig_prob A pointer to an array (size one for network migration) of migration probabilities.


If GA_MIG_NONE is selected the function will still create nislands 'islands' and will perform separate GAs on each of these sub-populations. As will be described later.


If any of these arguments are entered incorrectly, where possible, the function will revert these arguments to default values. The ParallelGeneticAlgorithm function firstly randomly creates initial populations on for island before evolving each of them separately.



4.4.0. Implementation of Migration Operators



4.4.1. What Technology Was Used?


Genetic algorithms are implicitly parallelisable, i.e. many of the operators can be carried out independently of each other. On multi-processor machines the (usually heavy) workload of calculating function evaluations can be split over each processor, as in the Master-Slave prototype of §3.2.


However, in order to allow for a number of different parallel implementations, perhaps the most straightforward way of parallelising the genetic algorithm function is to create separate populations evolving independently as separate sub-processes or 'islands'. After each generation the fittest individuals from each 'island' can then 'migrate' to other 'islands'.


In order to carry out this parallelisation two common methods used for implementing parallel code were considered - Message Passing and Threads.


Message passing (such as the MPI standard 1.1) is generally used for passing data between nodes or processors of distributed memory parallel machines. In terms of a parallel GA function this might mean passing the chromosome of an individual across a network connection from one processing node to another (i.e. from one 'island' to another).


Threads (such a the POSIX thread standard) are 'light weight' processes, that run on shared memory serial or parallel machines. 'Light weight' means that the system uses fewer resources in creating a threaded process than ordinary processes (e.g. created using the fork function call from the standard C library). The main difference between a process and a thread is as follows: A forked process, although an exact copy of its parent at the time it is created, has its own independent address space. A thread, on the other hand, shares the address space of its function arguments with its parent and with other threads.


Using an implementation combining both standards had had been considered. This had been shown to give a speed up in other areas. However, a decision was made by referring to (one of) the primary objectives for this GA function - that it can be easily implemented by the user in their program, keeping any special requirements on the part of the user or their specific set-up to a minimum.


Since MPI required the use of a special compiler (mpicc) and had to be run using its own seperate command (mpirun), It was felt that this would reduce the function's flexibility and ease of use. The disadvantage with threads was that they could only be run on shared memory systems, however, they are more portable than message passing systems and so this implementation was decided on.



4.4.2. Thread Implementation


Thread implementations that adhere to the IEEE POSIX 1003.1c standard (1995) are referred to as POSIX threads, or Pthreads. This standard was used to create and evolve each island sub-population. The function:


int pthread_create (pthread_t *thread, const pthread_attr_t *attr, 
		void*(*start_routine) (void), void *arg);

creates an instance of the pointer to the thread object thread, with attributes attr. The thread then executes the function start_routine, which has a single argument arg. Note that if start_routine needs more than one argument they must combined into a single structure before being passed to pthread_create.


In the parent function, ParallelGeneticAlgorithm(), the routine carried out by pthread_create() is GeneticAlgorithm(). This routine implements (without migration) one generation of a genetic algorithm using the parameters passed to the parent function. The code used was:


pthread_create(&island[i], NULL, (void*)GeneticAlgorithm, (void *)&args[i]);

Where island[i] is an instance of type pthread_t, i.e. a thread object. Setting attr to NULL uses the default thread attributes. (void *)&args[i] is a pointer (of type void) to a structure containing the arguments used by GeneticAlgorithm().


A separate thread is created by for each island. After scaling, selection, crossover and mutation each thread is joined using the function:


pthread_join(island[i], &rtrn_val);


Where rtrn_val receives the value returned by the routine GeneticAlgorithm - which is returns zero on success. This function is equivalent to waitpid() used in the fork() paradigm. It suspends execution of the parent process until all children (or, in the case of pthread_join(), threads) have returned.


When all threads have finished ParallelGeneticAlgorithm carries out any migration with the probability or probabilities specified by the user.


When migration has been carried out ParallelGeneticAlgorithm finds the fittest member from each island and stores the fittest of these.


This process of generating and joining threads and performing migration is repeated ngenerations times. If, after each generation, there is a fitter individual on any of the islands it replaces the previously stored fittest individual. Thus at the end of a run ParallelGeneticAlgorithm returns the fittest individual.



4.5. Conclusion


Hopefully now the operation and use of the parallel GA function will be clear to someone wishing to use the function. It should be clear that, because the field of genetic algorithms is constantly changing and becoming more complicated, it would be difficult to implement a function that could carry out some of the more unusual GA operators in addition to the more basic ones. Implementation of some of the more rarely used GA ideas would require relatively major rewriting of much of the code. Having the availability of diploid chromosomes, for example, would involve major overhauling of the crossover functions.


Having said that, it is hoped that the generic GA function would be useful for many problems that cannot be solved by other means.


The next chapter will demonstrate the speed up achieved using threaded implementation as opposed to an entirely serial implementation.

5.0. Results



5.1. Introduction


Having explained how the function ParallelGeneticAlgorithm() was implemented in parallel in the previous chapter, this chapter will show the speed up for a sample problem when implemented on a shared memory parallel machine. The chosen problem is one in game theory that has implications in the real world - the prisoners' dilemma.



5.2.0. The Prisoners' Dilemma using Parallel GA [MI96]


The prisoners' dilemma is a problem of conflicts and cooperation, drawn from political science and game theory. It is a simple two-person game invented by Merrill Flood and Melvin Dresher in the 1950s. It can be described as follows: Two individuals, A and B, are arrested for committing a crime together and placed in separate cells, with no communication between then possible. Prisoner A is offered the following deal: If he confesses and agrees to testify against prisoner B (i.e. Defects against B), he will receive a suspended sentence with probation (0 years) and prisoner B will receive 5 years. However, if at the same time prisoner B confesses and agrees to testify against A (i.e. B defects), A's testimony will be thrown out and both prisoners will receive 4 years. Both prisoners know that they are both offered this same deal. However, they also know that if neither testify (i.e. Both cooperate) they will both be convicted of a lesser charge for which they will only get 2 years.


By subtracting the number of years each player gets from the total possible (i.e. 5) we get the following pay-off matrix:


Player A\Player B

Cooperate

Defect

Cooperate

3, 3

0, 5

Defect

5, 0

1, 1


Without having any knowledge of what B is likely to do player A's best option is to defect - If he thinks B might cooperate then he should defect, sending B away for 5 years and getting away with a suspended sentence (receiving 5 points). If on the other hand A thinks B might defect, then he should still defect (and receive 1 point), and get lesser jail time than if he were to cooperate. The dilemma is that if both players defect they will both get a lesser score than if they both cooperate.


This becomes more apparent when the game is played a number of times, with each player knowing the others moves in previous iterations. If both players play 'logically', as above, they will choose to defect each time. However, the best overall strategy is for both players to cooperate, since this will yield the highest average score in the long run. How can reciprocal cooperation be introduced? The problem is an idealized model to 'real-world' arms races where defection and cooperation correspond to increasing and decreasing one's arsenal.


Robert Alexrod extensively studied this problem and invited researchers to submit playing strategies, which he then played against each other in a round-robin tournament. Each program remembered its opponents three previous moves, and in most cases decided it's next move on this basis.


Of the various strategies submitted, the winner (i.e. the strategy with the highest average score) was the simplest - Tit for Tat. This strategy offers cooperation in the first game and then does whatever its opponent did in the previous game. That is it offers cooperation and reciprocates it. But if the opponent defects then it punishes that defection with a defection of its own. It continues this until the other player cooperates again.



5.2.1. Encoding


The prisoners' dilemma problem above has a memory of three previous games. There are 26 = 64 possible combinations of this memory. This means there are also 64 different strategies possible. Thus a strategy for a prisoners' dilemma with a memory of 3 games can be encoded into a 64-bit string. A given strategies next move could be read from this string at the position corresponding to the value of the 6 bit memory expressed as an integer. If we then add the memory onto this string we get a 70bit string. This then becomes our chromosome for our GA.


5.2.2. Genetic Algorithm


The fitness of each strategy was calculated by playing each strategy against each other strategy in the population a set number of times. Adding the score and dividing by the number of population members calculates the fitness. In this problem there is no scaling required since all objective function values are positive and well spaced.


The following parameter values were chosen:


Population size 100 members

Number of generations 50

Selection Roulette Wheel

Scaling None

Elitism Yes, 5 elite members

Crossover Random, pc = 0.8

Mutation Yes, pmut = 0.01

Migration Network, pmig = 0.1


The GA consistently produced strategies that scored highly, in many cases looking quite similar to what a Tit for Tat strategy might look like (long sequences of 1's or 0's - i.e. cooperating as the opponent cooperates or defecting until the opponent cooperates).



Since the prisoners dilemma example was really only used for the purposes of showing a speed-up in the parallel implementation with respect to the same function in serial, the actual arguments were of little importance since they do not affect the relative speed of the parallel vs. serial implementations.



5.2.3. Serial Implementation


The serial implementation of the parallel function ParallelGeneticAlgorithm() was called MigratoryGeneticAlgorithm(). It worked in exctly the same way as its parallel counterpart except that the function GeneticAlgorithm() was called for each island in turn instead of being passed to individual threads.


5.2.4. Results


On a Dual 1GHz PIII system such as graves.maths.tcd.ie, the following speedup was observed on a range of islands (threads) form 1 to 40.










Fig 5.1. Speed-up of threaded vs unthreaded implementation of the prisoners dilema


It can be seen that the time taken to performs the GA on only one island population is slightly faster for the serial unthreaded implementation than for its threaded counterpart. This is due to the overhead required to set up the thread for each generation. This behaviour, however, is shown for the purposes of comparison only. For the case of one island in the function ParallelGeneticAlgorithm() there is no thread created, so this time difference does not exist. As can be seen for 2 or more threads there is a significant speed-up on this 2-processor machine.


On the single processor 400MHz Pentium II machine, Turing, the following results were observed:




Fig 5.2. Slow-down of threaded vs. unthreaded implementation of the prisoners’ dilemma


Here we can see a relative slow-down using threads on a single processor machine, again due to the computational overhead required to create each thread for each generation.


Finally, on a 2 1Ghz processor Pentium III (Coppermine) node of a dedicated parallel machine (i.e. where there are no other processes running at the same time) we can again see an even more significant speed-up:




Fig 5.3. Speed-up of threaded vs unthreaded implementation of the prisoners dilema on a dedicated parallel machine


Without interruption the function performs even better.

5.3. Conclusion


The above results have shown that function ParallelGeneticAlgorithm() gets faster when run over on a shared memory multiple processor machine. On a single processor machine where no threads are created the function is simply a serial program.


As clock speeds of processors reach theoretical limits multiple processor shared memory machines will become the norm. On these machines, where there are many more processors a significant speed-up would be observed for this function.

6.0. Conclusions and Future Directions



6.1. Introduction


It is hoped that this report has served as both a introduction to both genetic algorithms and as guide to using the library of functions prototyped in ga.h. It is also hoped that the GA functions can be of some use in solving certain problems and in modelling natural evolutionary phenomena. As in many newly emerging fields, there is constant research into new and more elaborate methods of implementing genetic algorithms and so it would be impossible to have a generic GA offering all possible operators. The next section, however, will briefly describe some of these newer ideas, showing future directions for genetic algorithms.



6.2. Future Directions


Holland's Adaptation in Natural and Artificial Systems was one of the first attempts to set down a general framework for adaptation in nature and in computers. Many of the operators and options used in this project were taken either directly or indirectly from this text.


However, research into various other implementations has been carried out. Scope for improvement could come from the following areas:

Further ideas from genetics:


Perhaps the most obvious way of improving a genetic algorithm is to look again to nature. In particular implementations involving the following could be used:


Multiple diploid chromosome genotypes. These are genotypes having multiple pairs of chromosomes instead of just one chromosome. Related to selection and crossover for these multiple chromosomes is segregation and translocation [GO89]. Dominance is the process whereby certain genes are more prevalent than others causing them to appear phenotypicly more than others in the genotype. In natural systems duplication and deletion are the processes that cause mutation in genes. Duplication is the copying of a particular gene and placing it on the chromosome alongside the original. Deletion serves to remove duplicated genes from the chromosome. Errors in these processes cause mutation. Sexual determination and differentiation – where organisms have two (or more) distinct sexes which come together in some way to propagate the species - could also be introduced, although it's benefits are unclear in terms of artificial genetic search except perhaps, as a model of natural systems.



Incorporation of development and learning


In natural evolution there is a separation between genotypes (encodings) and phenotypes (candidate solutions). The process of development and learning can help tune the behavioural parameters of an organism, defined by its genome so that it can adapt to its particular environment. If these parameters were to be decided completely by its genome alone then the individual could not adapt to a changing environment during its life. Modelling and implementing these natural processes into evolutionary computing could create far more efficient algorithms. One such similar example is a hybrid genetic algorithm that uses the GA to get close to the solution and another search method, such as hill climbing, to find the exact solution.



Variable length genotype encoding


Evolution in nature not only changes the fitness of organisms, it also changes the way genes are encoded. Genotypes have increases in size over evolutionary time. The ability of a GA to adapt its own encoding has been shown to be important in order for GAs to evolve complex structures [MI96].



Adapting Parameters


Natural evolution constantly adapts its own parameters. Crossover and mutation rates are encoded in the genomes of organisms. Likewise, population sizes in nature are not constant but are controlled by complicated ecological interactions. Thus the ability to change the parameters of a GA during it's run is highly desirable. At different stages of the run different values of crossover or mutation rates are sometimes needed as this can even prevent the algorithm from converging prematurely or stagnating. Having an algorithm that could adapt these parameters itself, as they are required, would be a major step in the right direction.



6.3. Conclusion


As the field of evolutionary computing continues to grow algorithms become more and more involved. As is described above, genetic algorithms will, in the future, more closely model natural genetic systems. Whether or not this will lead to artificially intelligent machines remains to be seen.

References


[HO75] Holland, J. 1975 Adaptation in Natural and Artificial Systems. Addison-Wesley.


[MI96] Mitchell, M. 1996 An introduction to Genetic Algorithms. MIT Press.


[GO89] Goldberg, D.E. 1989 Genetic Algorithms in Searc, Optimization and Machine Learning. Addison-Wesley.


[GR86] Grefenstette, J.J. 1986 Optimization of control parameters for genetic Algorithms.


[GR89] Grefenstette, J.J. 1989 How Genetic Algorithms work: A critical look at implicit parallelism.


[CO99] Coley D.A. 1999 An Introduction to Genetic Algorithms for Scientists and Engineers. World Scientific Publishing.


Dr. C.J. Burgess, University of Bristol. Evolutionary Computing http://www.cs.bris.ac.uk/%7Ecolin/evollect1/index.htm


Dr Paul Brna, Lancaster University. Introduction to AI Programming

http://www.comp.lancs.ac.uk/computing/research/aai- aied/people/paulb/old243prolog/243notes96.html


Brunel University Artificial Intelligence Site

http://www.brunel.ac.uk/research/AI/alife/ga-axelr.htm