Christian Huygens (1629 - 1695)
From `A Short Account of the History of Mathematics' (4th edition, 1908)
by W. W. Rouse Ball.
Christian Huygens was born at the Hague on April 14, 1629,
and died in the same town on July 8, 1695. He generally wrote his
name as Hugens, but I follow the usual custom in spelling it as
above: it is also sometimes written as Huyghens. His life was
uneventful, and there is little more to record in it than a
statement of his various memoirs and researches.
In 1651 he published an essay in which he shewed the fallacy in a
system of quadratures proposed by Grégoire de Saint-Vincent,
who was well versed in the geometry of the Greeks, but had not
grasped the essential points in the more modern methods. This
essay was followed by tracts on the quadrature of the conics and
the approximate rectification of the circle.
In 1654 his attention was directed to the improvement of the
telescope. In conjunction with his brother he devised a new
and better way of grinding and polishing lenses. As a result
of these improvements he was able during the following two years,
1655 and 1656, to resolve numerous astronomical questions; as,
for example, the nature of Saturn's appendage. His astronomical
observations required some exact means of measuring time, and he
was thus led in 1656 to invent the pendulum clock, as described
in his tract Horologium, 1658. The time-pieces previously
in use had been balance-clocks.
In the year 1657 Huygens wrote a small work on the calculus of
probabilities founded on the correspondence of Pascal and Fermat.
He spent a couple of years in England about this time. His
reputation was now so great that in 1665 Louis XIV. offered him
a pension if he would live in Paris, which accordingly then
became his place of residence.
In 1668 he sent to the Royal Society of London, in answer to a
problem they had proposed, a memoir in which (simultaneously with
Wallis and Wren) he proved by experiment that the momentum in a
certain direction before the collision of two bodies is equal to
the momentum in that direction after the collision. This was
one of the points in mechanics on which Descartes had been
mistaken.
The most important of Huygens's work was his Horologium
Oscillatorium published at Paris in 1673. The first
chapter is devoted to pendulum clocks. The second chapter
contains a complete account of the descent of heavy bodies
under their own weights in a vacuum, either vertically down
or on smooth curves. Amongst other propositions he shews that
the cycloid is tautochronous. In the third chapter he defines
evolutes and involutes, proves some of their more elementary
properties, and illustrates his methods by finding the evolutes
of the cycloid and the parabola. These are the earliest instances
in which the envelope of a moving line was determined. In the fourth
chapter he solves the problem of the compound pendulum, and shews that
the centres of oscillation and suspension are interchangeable. In the
fifth and last chapter he discusses again the theory of clocks, points
out that if the bob of the pendulum were, by means of cycloidal clocks,
made to oscillate in a cycloid the oscillations would be isochronous;
and finishes by shewing that the centrifugal force on a body which moves
around a circle of radius r with a uniform velocity v varies
directly as
v²
and inversely as r. This work contains the first
attempt to apply dynamics to bodies of finite size, and not merely to
particles.
In 1675 Huygens proposed to regulate the motion of watches by the use
of the balance spring, in the theory of which he had been perhaps
anticipated in a somewhat ambiguous and incomplete statement made
by Hooke in 1658. Watches or portable clocks had been invented early
in the sixteenth century, and by the end of that century were not very
uncommon, but they were clumsy and unreliable, being driven by a
main spring and regulated by a conical pulley and verge escapement;
moreover, until 1687 they had only one hand. The first watch whose
motion was regulated by a balance spring was made at Paris under
Huygens's directions, and presented by him to Louis XIV.
The increasing intolerance of the Catholics led to his return to
Holland in 1681, and after the revocation of the edict of Nantes
he refused to hold any further communication with France. He now
devoted himself to the construction of lenses of enormous focal
length: of these three of focal lengths 123 feet, 180 feet, and
210 feet, were subsequently given by him to the Royal Society of
London, in whose possession they still remain. It was about this
time that he discovered the achromatic eye-piece (for a telescope)
which is known by his name. In 1689 he came from Holland to England
in order to make the acquaintance of Newton, whose Principia
had been published in 1687. Huygens fully recognized the intellectual
merits of the work, but seems to have deemed any theory incomplete
which did not explain gravitation by mechanical means.
On his return in 1690 Huygens published his treatise on light
in which the undulatory theory was expounded and explained. Most of
this had been written as early as 1678. The general idea of the
theory had been suggested by Robert Hooke in 1664, but he had not
investigated its consequences in any detail. Only three ways have
been suggested in which light can be produced mechanically. Either
the eye may be supposed to send out something which, so to speak,
feels the object (as the Greeks believed); or the object perceived
may send out something which hits or affects the eye (as assumed in
the emission theory); or there may be some medium between the eye
and the object, and the object may cause some change in the form or
condition of this intervening medium and thus affect the eye (as
Hooke and Huygens supposed in the wave or undulatory theory).
According to this last theory space is filled with an extremely
rare ether, and light is caused by a series of waves or vibrations
in this ether which are set in motion by the pulsations of the
luminous body. From this hypothesis Huygens deduced the laws of
reflexion and refraction, explained the phenomenon of double
refraction, and gave a construction for the extraordinary ray in
biaxal crystals; while he found by experiment the chief phenomena
of polarization.
The immense reputation and unrivalled powers of Newton led to
disbelief in a theory which he rejected, and to the general adoption
of Newton's emission theory. Within the present century crucial
experiments have been devised which give different results according
as one or the other theory is adopted; all these experiments agree
with the results of the undulatory theory and differ from the results
of the Newtonian theory; the latter is therefore untenable. Until,
however, the theory of interference, suggested by Young, was worked
out by Fresnel, the hypothesis of Huygens failed to account for all
the facts, and even now the properties which, under it, have to be
attributed to the intervening medium or ether involve difficulties
of which we still seek a solution. Hence the problem as to how the
effects of light are really produced cannot be said to be finally
solved.
Besides these works Huygens took part in most of the controversies
and challenges which then played so large a part in the mathematical
world, and wrote several minor tracts. In one of these he investigated
the form and properties of the catenary. In another he stated in
general terms the rule for finding maxima and minima of which Fermat
had made use, and shewed that the subtangent of an algebraical
curve f(x,y) = 0 was equal to
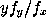 ,
where
,
where
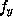 is the derived function of f(x,y) regarded as
a function of y. In some posthumous works, issued at Leyden
in 1703, he further shewed how from the focal lengths of the
component lenses the magnifying power of a telescope could be
determined; and explained some of the phenomena connected with
haloes and parhelia.
is the derived function of f(x,y) regarded as
a function of y. In some posthumous works, issued at Leyden
in 1703, he further shewed how from the focal lengths of the
component lenses the magnifying power of a telescope could be
determined; and explained some of the phenomena connected with
haloes and parhelia.
I should add that almost all his demonstrations, like those of Newton,
are rigidly geometrical, and he would seem to have made no use of the
differential or fluxional calculus, though he admitted the validity
of the methods used therein. Thus, even when first written, his works
were expressed in an archaic language, and perhaps received less
attention than their intrinsic merits deserved.
This page is included in a
collection of mathematical biographies taken from
A Short Account of the History of Mathematics
by W. W. Rouse Ball (4th Edition, 1908).
Transcribed by
D.R. Wilkins
(dwilkins@maths.tcd.ie)
School of Mathematics
Trinity College, Dublin
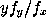 ,
where
,
where
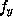 is the derived function of f(x,y) regarded as
a function of y. In some posthumous works, issued at Leyden
in 1703, he further shewed how from the focal lengths of the
component lenses the magnifying power of a telescope could be
determined; and explained some of the phenomena connected with
haloes and parhelia.
is the derived function of f(x,y) regarded as
a function of y. In some posthumous works, issued at Leyden
in 1703, he further shewed how from the focal lengths of the
component lenses the magnifying power of a telescope could be
determined; and explained some of the phenomena connected with
haloes and parhelia.