 .
.
From `A Short Account of the History of Mathematics' (4th edition, 1908) by W. W. Rouse Ball.
Leonhard Euler was born at Bâle on April 15, 1707, and died at St. Petersburg on September 7, 1783. he was the son of a Lutheran minister who had settled at Bâle, and was educated in his native town under the direction of John Bernoulli, with whose sons Daniel and Nicholas he formed a lifelong friendship. When, in 1725, the younger Bernoullis went to Russia, on the invitation of the empress, they procured a place there for Euler, which in 1733 he exchanged for the chair of mathematics, then vacated by Daniel Bernoulli. The severity of the climate affected his eyesight, and in 1735 he lost the use of one eye completely. In 1741 he moved to Berlin at the request, or rather command, of Frederick the Great; here he stayed till 1766, when he returned to Russia, and was succeeded at Berlin by Lagrange. Within two or three years of his going back to St. Petersburg he became blind; but in spite of this, and although his house, together with many of his papers, were burnt in 1771, he recast and improved most of his earlier works. He died of apoplexy in 1783. He was married twice.
I think we may sum up Euler's work by saying that he created a good deal of analysis, and revised almost all the branches of pure mathematics which were then known, filling up the details, adding proofs, and arranging the whole in a consistent form. Such work is very important, and it is fortunate for science when it fall into hands as competent as those of Euler.
Euler wrote an immense number of memoirs on all kinds of mathematical subjects. His chief works, in which many of the results of earlier memoirs are embodied, are as follows.
In the first place, he wrote in 1748 his Introductio in Analysin Infinitorum, which was intended to serve as an introduction to pure analytical mathematics. This is divided into two parts.
The first part of the Analysis Infinitorum contains the bulk
of the matter which is to be found in modern text-books on algebra,
theory of equations, and trigonometry. In the algebra he paid
particular attention to the expansion of various functions in series,
and to the summation of given series; and pointed out explicitly that
an infinite series cannot be safely employed unless it is convergent.
In the trigonometry, much of which is founded on F. C. Mayer's
Arithmetic of Sines, which had been published in 1727, Euler
developed the idea of John Bernoulli, that the subject was a branch of
analysis and not a mere appendage of astronomy or geometry. he also
introduced the trigonometrical functions, and shewed that the
trigonometrical and exponential functions were connected by the
relation
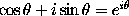 .
.
Here, too [pp. 85, 90, 93], we meet the symbol e used to denote the
base of the Napierian logarithms, namely, the incommensurable number
2.71828..., and the symbol
 used to denote the incommensurable number 3.14159.... The use of a
single symbol to denote the number 2.71828... seems to be due to Cotes,
who denoted it by M; Euler in 1731 denoted it by e. To
the best of my knowledge, Newton had been the first to employ the
literal exponential notation, and Euler, using the form
used to denote the incommensurable number 3.14159.... The use of a
single symbol to denote the number 2.71828... seems to be due to Cotes,
who denoted it by M; Euler in 1731 denoted it by e. To
the best of my knowledge, Newton had been the first to employ the
literal exponential notation, and Euler, using the form
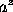 ,
had taken a as the base of any system of logarithms. It is
probable that the choice of e for a particular base was
determined by its being the vowel consecutive to a. The use of
a single symbol to denote the number 3.14159... appears to have been
introduced about the beginning of the eighteenth century. W. Jones in
1706 represented it by
,
had taken a as the base of any system of logarithms. It is
probable that the choice of e for a particular base was
determined by its being the vowel consecutive to a. The use of
a single symbol to denote the number 3.14159... appears to have been
introduced about the beginning of the eighteenth century. W. Jones in
1706 represented it by
 ,
a symbol which had been used by Oughtred in 1647, and by Barrow a few
years later, to denote the periphery of a circle. John Bernoulli
represented the number by c; Euler in 1734 denoted by p,
and in a letter of 1736 (in which he enunciated the theorem that the
sum of the squares of the reciprocals of the natural numbers is
,
a symbol which had been used by Oughtred in 1647, and by Barrow a few
years later, to denote the periphery of a circle. John Bernoulli
represented the number by c; Euler in 1734 denoted by p,
and in a letter of 1736 (in which he enunciated the theorem that the
sum of the squares of the reciprocals of the natural numbers is
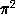 /6)
he used the letter c; Chr. Goldbach in 1742 used
/6)
he used the letter c; Chr. Goldbach in 1742 used
 ;
and after the publication of Euler's Analysis the symbol
;
and after the publication of Euler's Analysis the symbol
 was generally employed.
was generally employed.
The numbers e and
 would enter into mathematical analysis from
whatever side the subject was approached. The latter represents
among other things the ratio of the circumference of a circle to its
diameter, but it is a mere accident that that is taken for its
definition. De Morgan in the Budget of Paradoxes tells an
anecdote which illustrates how little the usual definition suggests
its real origin. He was explaining to an actuary what was the chance
that at the end of a given time a certain proportion of some group of
people would be alive; and quoted the actuarial formula involving
would enter into mathematical analysis from
whatever side the subject was approached. The latter represents
among other things the ratio of the circumference of a circle to its
diameter, but it is a mere accident that that is taken for its
definition. De Morgan in the Budget of Paradoxes tells an
anecdote which illustrates how little the usual definition suggests
its real origin. He was explaining to an actuary what was the chance
that at the end of a given time a certain proportion of some group of
people would be alive; and quoted the actuarial formula involving
 ,
which, in answer to a question, he explained stood for the
ratio of the circumference of a circle to its diameter. His
acquaintance, who had so far listened to the explanation with
interest, interrupted him and explained, ``My dear friend, that must
be a delusion; what can a circle have to do with the number of people
alive at the end of a given time?''
,
which, in answer to a question, he explained stood for the
ratio of the circumference of a circle to its diameter. His
acquaintance, who had so far listened to the explanation with
interest, interrupted him and explained, ``My dear friend, that must
be a delusion; what can a circle have to do with the number of people
alive at the end of a given time?''
The second part of the Analysis Infinitorum is on analytical geometry. Euler commenced this part by dividing curves into algebraical and transcendental, and established a variety of propositions which are true for all algebraical curves. He then applied these to the general equation of the second degree in two dimensions, shewed that it represents the various conic sections, and deduced most of their properties from the general equation. he also considered the classification of cubic, quartic and other algebraical curves. He next discussed the question as to what surfaces are represented by the general equation of the second degree in three dimensions, and how they may be discriminated one from the other: some of these surfaces had not been previously investigated. in the course of this analysis he laid down the rules for the transformation of co-ordinates in space. Here also we find the earliest attempt to bring the curvature of surfaces within the domain of mathematics, and the first complete discussion of tortuous curves.
The Analysis Infinitorum was followed in 1755 by the Institutiones Calculi Differentialis, to which it was intended as an introduction. This is the first text-book on the differential calculus which has any claim to be regarded as complete, and it may be said that until recently many modern treatises on the subject are based on it; at the same time it should be added that the exposition of the principles of the subject is often prolix and obscure, and sometimes not altogether accurate.
This series of works was completed by the publication in three volumes in 1768 to 1770 of the Institutiones Calculi Integralis, in which the results of several of Euler's earlier memoirs on the same subject and on differential equations are included. This, like the similar treatise on the differential calculus, summed up what was then known on the subject, but many of the theorems were recast and the proofs improved. The Beta and Gamma functions were invented by Euler and are discussed here, but only as illustrations of methods of reduction and integration. His treatment of elliptic integrals is superficial; it was suggested by a theorem, given by John Landen in the Philosophical Transactions for 1775, connecting the arcs of a hyperbola and an ellipse. Euler's works that form this trilogy have gone through numerous subsequent editions.
The classic problems on isoperimetrical curves, the brachistochrone in a resisting medium, and the theory of geodesics (all of which had been suggested by his master, John Bernoulli) had engaged Euler's attention at an early date; and in solving them he was led to the calculus of variations. The general idea of this was laid down in his Curvarum Maximi Minimive Proprietate Gaudentium Inventio Nova ac Facilis, published in 1744, but the complete development of the new calculus was first effected by Lagrange in 1759. The method used by Lagrange is described in Euler's integral calculus, and is the same as that given in most modern text-books on the subject.
In 1770 Euler published his Anleitung zur Algebra in two volumes. A French translation, with numerous and valuable additions by Lagrange, was brought out in 1794; and a treatise on arithmetic by Euler was appended to it. The first volume treats of determinate algebra. This contains one of the earliest attempts to place the fundamental processes on a scientific basis: the same subject had attracted D'Alembert's attention. This work also includes the proof of the binomial theorem for an unrestricted real index which is still known by Euler's name; the proof is founded on the principle of the permanence of equivalent forms, but Euler made no attempt to investigate the convergency of the series: that he should have omitted this essential step is the more curious as he had himself recognized the necessity of considering the convergency of infinite series: Vandermonde's proof given in 1764 suffers from the same defect.
The second volume of the algebra treats of indeterminate or Diophantine algebra. This contains the solutions of some of the problems proposed by Fermat, and which had hitherto remained unsolved.
As illustrating the simplicity and directness of Euler's methods I
give the substance of his demonstration, alluded to above,
that all even perfect numbers are included in Euclid's formula,
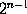 p,
where p stands for
p,
where p stands for
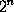 - 1
and is a prime.
Let N be an even perfect number. N is even, hence it can be
written in the form
- 1
and is a prime.
Let N be an even perfect number. N is even, hence it can be
written in the form
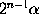 ,
where
,
where
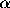 is not divisible
by 2. N is perfect, that is, is equal to the sum of all its
integral subdivisors; therefore (if the number itself be reckoned as
one of its divisors) it is equal to half the sum of all its integral
divisors, which we may denote by
is not divisible
by 2. N is perfect, that is, is equal to the sum of all its
integral subdivisors; therefore (if the number itself be reckoned as
one of its divisors) it is equal to half the sum of all its integral
divisors, which we may denote by
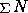 .
Since 2N=
.
Since 2N=
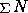 ,
we have
,
we have
therefore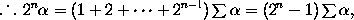
Hence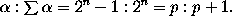
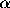 =
=
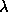 p
and
p
and
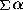 =
=
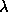 (p + 1);
and since the ratio p : p + 1 is in its lowest terms,
(p + 1);
and since the ratio p : p + 1 is in its lowest terms,
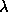 must be a positive integer. Now, unless
must be a positive integer. Now, unless
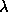 = 1, we have 1,
= 1, we have 1,
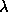 ,
p and
,
p and
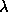 p
as factors of
p
as factors of
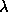 p;
moreover if, p be not prime, there will be other factors also.
Hence, unless
p;
moreover if, p be not prime, there will be other factors also.
Hence, unless
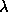 = 1 and p be a prime, we have
= 1 and p be a prime, we have
But this is inconsistent with the result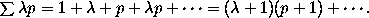
Hence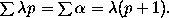
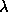 must be equal to 1 and p must be prime. Therefore
must be equal to 1 and p must be prime. Therefore
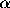 = p, therefore
= p, therefore
I may add the corollary that since p is a prime, it follows that n is a prime; and the determination of what values of n (less than 257) make p prime falls under Mersenne's rule.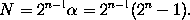
The four works mentioned above comprise most of what Euler produced in pure mathematics. He also wrote numerous memoirs on nearly all the subjects of applied mathematics and mathematical physics then studied: the chief novelties in them are as follows.
In the mechanics of a rigid system he determined the general equations of motion of a body about a fixed point, which are ordinarily written in the form
and he gave the general equations of motion for a free body, which are usually presented in the form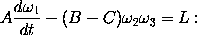
He also defended and elaborated the theory of ``least action'' which had been propounded by Maupertuis in 1751 in his Essai de cosmologie [p. 70].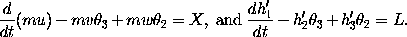
In hydrodynamics Euler established the general equations of motion, which are commonly expressed in the form
At the time of his death he was engaged in writing a treatise on hydromechanics in which the treatment of the subject would have been completely recast.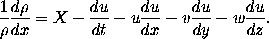
His most important works on astronomy are his Theoria Motuum Planetarum et Cometarum, published in 1744; his Theoria Motus Lunaris, published in 1753; and his Theoria Motuum Lunae, published in 1772. In these he attacked the problem of three bodies: he supposed the body considered (ex. gr. the moon) to carry three rectangular axes with it in its motion, the axes moving parallel to themselves, and to these axes all the motions were referred. This method is not convenient, but it was from Euler's results that Mayer constructed the lunar tables for which his widow in 1770 received 5000 pounds from the English parliament, and in recognition of Euler's services a sum of 300 pounds was also voted as an honorarium to him.
Euler was much interested in optics. In 1746 he discussed the relative merits of the emission and undulatory theories of light; he on the whole preferred the latter. In 1770--71 he published his optical researches in three volumes under the title Dioptrica.
He also wrote and elementary work on physics and the fundamental principles of mathematical philosophy. This originated from an invitation he received when he first went to Berlin to give lessons on physics to the princess of Anhalt-Dessau. These lectures were published in 1768--1772 in three volumes under the title Lettres ... sur quelques sujets de physique ..., and for half a century remained a standard treatise on the subject.
This page is included in a collection of mathematical biographies taken from A Short Account of the History of Mathematics by W. W. Rouse Ball (4th Edition, 1908).
Transcribed by