René Descartes (1596 - 1650)
From `A Short Account of the History of Mathematics' (4th edition, 1908)
by W. W. Rouse Ball.
We may consider Descartes as the first
of the modern school of mathematics. René Descartes
was born near Tours on March 31, 1596, and died at Stockholm on
February 11, 1650; thus he was a contemporary of Galileo and
Desargues. His father, who, as the name implies, was of good
family, was accustomed to spend half the year at Rennes when the
local parliament, in which he held a commission as councillor,
was in session, and the rest of the time on his family estate of
Les Cartes at La Haye. René, the second of a family
of two sons and one daughter, was sent at the age of eight years
to the Jesuit School at La Flêche, and of the admirable discipline
and education there given he speaks most highly. On account of
his delicate health he was permitted to lie in bed till late in the
mornings; this was a custom which he always followed, and when he
visited Pascal in 1647 he told him that the only way to do good
work in mathematics and to preserve his health was never to allow
anyone to make him get up in the morning before he felt inclined
to do so; an opinion which I chronicle for the benefit of any
schoolboy into whose hands this work may fall.
On leaving school in 1612 Descartes went to Paris to be introduced
to the world of fashion. Here, through the medium of the Jesuits,
he made the acquaintance of Mydorge, and renewed his schoolboy
friendship with Mersenne, and together with them he devoted the two
years of 1615 and 1616 to the study of mathematics. At that time
a man of position usually entered either the army or the church;
Descartes chose the former profession, and in 1617 joined the army
of Prince Maurice of Orange, then at Breda. Walking through the
streets there he saw a placard in Dutch which excited his curiosity,
and stopping the first passer, asked him to translate it into either
French or Latin. The stranger, who happened to be Isaac Beeckman,
the head of the Dutch College at Dort, offered to do so if Descartes
would answer it; the placard being, in fact, a challenge to all the
world to solve a certain geometrical problem. Descartes worked it out
within a few hours, and a warm friendship between him and Beeckman was
the result. This unexpected test of his mathematical attainments made
the uncongenial life of the army distasteful to him, but under family
influence and tradition he remained a soldier, and was persuaded at
the commencement of the Thirty Years' War to volunteer under
Count de Bucquoy in the army of Bavaria. He continued all this time
to occupy his leisure with mathematical studies, and was accustomed
to date the first ideas of his new philosophy and of his analytical
geometry from three dreams which he experienced on the night of
November 10, 1619, at Neuberg, when campaigning on the Danube. He
regarded this as the critical day of his life, and one which determined
his whole future.
He resigned his commission in the spring of 1621, and spent the next
five years in travel, during most of which time he continued to study
pure mathematics. In 1626 we find him settled at Paris, ``a little
well-built figure, modestly clad in green taffety, and only wearing
sword and feather in token of his quality as a gentleman.'' During
the first two years there he interested himself in general society,
and spent his leisure in the construction of optical instruments;
but these pursuits were merely the relaxations of one who failed to
find in philosophy that theory of the universe which he was convinced
finally awaited him.
In 1628 Cardinal de Berulle, the founder of the Oratorians, met
Descartes, and was so much impressed by his conversation that he
urged on him the duty of devoting his life to the examination of
truth. Descartes agreed, and the better to secure himself from
interruption moved to Holland, then at the height of his power.
There for twenty years he lived, giving up all his time to
philosophy and mathematics. Science, he says, may be compared to
a tree; metaphysics is the root, physics is the trunk, and the
three chief branches are mechanics, medicine, and morals, these
forming the three applications of our knowledge, namely, to the
external world, to the human body, and to the conduct of life.
He spend the first four years, 1629 to 1633, of his stay in Holland
in writing Le Monde, which embodies an attempt to give a
physical theory of the universe; but finding that its publication
was likely to bring on him the hostility of the church, and having
no desire to pose as a martyr, he abandoned it: the incomplete
manuscript was published in 1664. He then devoted himself to
composing a treatise on universal science; this was published
at Leyden in 1637 under the title Discours de la méthode
pour bien conduire sa raison et chercher la vérité dans
les sciences, and was accompanied with three appendices (which
possibly were not issued till 1638) entitled La Dioptrique,
Les Météores, and La Géométrie; it
is from the last of these that the invention of analytical geometry
dates. In 1641 he published a work called Meditationes, in
which he explained at some length his views on philosophy as sketched
out in the Discours. In 1644 he issued the Principia
Philosophiae, the greater part of which was devoted to physical
science, especially the laws of motion and the theory of vortices.
In 1647 he received a pension from the French court in honour of
his discoveries. He went to Sweden on the invitation of the Queen
in 1649, and died a few months later of inflammation of the lungs.
In appearance, Descartes was a small man with large head, projecting
brow, prominent nose, and black hair coming down to his eyebrows.
His voice was feeble. In disposition he was cold and selfish.
Considering the range of his studies he was by no means widely read,
and he despised both learning and art unless something tangible could
be extracted therefrom. He never married, and left no descendants,
though he had one illegitimate daughter, who died young.
As to his philosophical theories, it will be sufficient to say that
he discussed the same problems which have been debated for the last
two thousand years, and probably will be debated with equal zeal
two thousand years hence. It is hardly necessary to say that the
problems themselves are of importance and interest, but from the
nature of the case no solution ever offered is capable either of
rigid proof or of disproof; all that can be effected is to make one
explanation more probable than another, and whenever a philosopher
like Descartes believes that he has at last finally settled a question
it has been possible for his successors to point out the fallacy in
his assumptions. I have read somewhere that philosophy has always
been chiefly engaged with the inter-relations of God, Nature, and Man.
The earliest philosophers were Greeks who occupied themselves mainly
with the relations between God and Nature, and dealt with Man
separately. The Christian Church was so absorbed in the relation of
God to Man as entirely to neglect Nature. Finally, modern philosophers
concern themselves chiefly with the relations between Man and Nature.
Whether this is a correct historical generalization of the views which
have been successively prevalent I do not care to discuss here, but
the statement as to the scope of modern philosophy marks the limitations
of Descartes's writings.
Descartes's chief contributions to mathematics were his analytical
geometry and his theory of vortices, and it is on his researches
in connection with the former of these subjects that his mathematical
reputation rests.
Analytical geometry does not consist merely (as is sometimes loosely
said) in the application of algebra to geometry; that had been done
by Archimedes and many others, and had become the usual method of
procedure in the works of the mathematicians of the sixteenth
century. The great advance made by Descartes was that he saw that
a point in a plane could be completely determined if its distances,
say x and y, from two fixed lines drawn at right
angles in the plane were given, with the convention familiar to us
as to the interpretation of positive and negative values; and that
though an equation f(x,y) = 0 was indeterminate and
could be satisfied by an infinite number of values of x and
y, yet these values of x and y determined the
co-ordinates of a number of points which form a curve, of which
the equation f(x,y) = 0 expresses some geometrical
property, that is, a property true of the curve at every point on
it. Descartes asserted that a point in space could be similarly
determined by three co-ordinates, but he confined his attention to
plane curves.
It was at once seen that in order to investigate the properties of
a curve it was sufficient to select, as a definition, any
characteristic geometrical property, and to express it by means
of an equation between the (current) co-ordinates of any point
on the curve, that is, to translate the definition into the
language of analytical geometry. The equation so obtained
contains implicitly every property of the curve, and any particular
property can be deduced from it by ordinary algebra without troubling
about the geometry of the figure. This may have been dimly recognized
or foreshadowed by earlier writers, but Descartes went further and
pointed out the very important facts that two or more curves can
be referred to one and the same system of co-ordinates, and that
the points in which two curves intersect can be determined by finding
the roots common to their two equations. I need not go further into
details, for nearly everyone to whom the above is intelligible will
have read analytical geometry, and is able to appreciate the value
of its invention.
Descartes's Géométrie is divided into three books:
the first two of these treat of analytical geometry, and the third
includes an analysis of the algebra then current. It is somewhat
difficult to follow the reasoning, but the obscurity was intentional.
``Je n'ai rien omis.'' says he, ``qu'à dessein ... j'avois
prévu que certaines gens qui se vantent de sçavoir tout
n'auroient par manqué de dire que je n'avois rien écrit
qu'ils n'eussent sçu auparavant, si je me fusse rendu assez
intelligible pour eux.''
The first book commences with an explanation of the principles of
analytical geometry, and contains a discussion of a certain problem
which had been propounded by Pappus in the seventh book of his
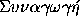 and of which some particular cases had been considered by Euclid
and Apollonius. The general theorem had baffled previous
geometricians, and it was in the attempt to solve it that Descartes
was led to the invention of analytical geometry. The full enunciation
of the problem is rather involved, but the most important case is
to find the locus of a point such that the product of the perpendiculars
on m given straight lines shall be in a constant ratio to
the product of the perpendiculars on n other given straight
lines. The ancients had solved this geometrically for the case
m = 1, n = 1, and the case m = 1, n = 2.
Pappus had further stated that, if m = n = 2, the
locus is a conic, but he gave no proof; Descartes also failed to
prove this by pure geometry, but he shewed that the curve is
represented by an equation of the second degree, that is, a conic;
subsequently Newton gave an elegant solution of the problem by pure
geometry.
and of which some particular cases had been considered by Euclid
and Apollonius. The general theorem had baffled previous
geometricians, and it was in the attempt to solve it that Descartes
was led to the invention of analytical geometry. The full enunciation
of the problem is rather involved, but the most important case is
to find the locus of a point such that the product of the perpendiculars
on m given straight lines shall be in a constant ratio to
the product of the perpendiculars on n other given straight
lines. The ancients had solved this geometrically for the case
m = 1, n = 1, and the case m = 1, n = 2.
Pappus had further stated that, if m = n = 2, the
locus is a conic, but he gave no proof; Descartes also failed to
prove this by pure geometry, but he shewed that the curve is
represented by an equation of the second degree, that is, a conic;
subsequently Newton gave an elegant solution of the problem by pure
geometry.
In the second book Descartes divides curves into two classes,
namely, geometrical and mechanical curves. He defines geometrical
curves as those which can be generated by the intersection of two
lines each moving parallel to one co-ordinate axis with ``commensurable''
velocities; by which terms he means that dy/dx is an
algebraical function, as, for example, is the case in the ellipse
and the cissoid. He calls a curve mechanical when the ratio of
the velocities of these lines is ``incommensurable''; by which term
he means that dy/dx is a trancendental function,
as, for example, is the case in the cycloid and the quadratrix.
Descartes confined his discussion to geometrical curves, and did not
treat of the theory of mechanical curves. The classification into
algebraical and transcendental curves now usual is due to Newton.
Descartes also paid particular attention to the theory of the
tangents to curves - as perhaps might be inferred from his
system of classification just alluded to. The then current
definition of a tangent at a point was a straight line through
the point such that between it and the curve no other straight
line could be drawn, that is, the straight line of closest
contact. Descartes proposed to substitute for this a statement
equivalent to the assertion that the tangent is the limiting
position of the secant; Fermat, and at a later date Maclaurin
and Lagrange, adopted this definition. Barrow, followed by
Newton and Leibnitz, considered a curve as the limit of an
inscribed polygon when the sides become indefinitely small,
and stated that the side of the polygon when produced became
in the limit a tangent to the curve. Roberval, on the other
hand, defined a tangent at a point as the direction of motion
at that instant of a point which was describing the curve.
The results are the same whichever definition is selected,
but the controversy as to which definition was the correct one
was none the less lively. In his letters Descartes illustrated
his theory by giving the general rule for drawing tangents and
normals to a roulette.
The method used by Descartes to find the tangent or normal at any
point of a given curve was substantially as follows. He determined
the centre and radius of a circle which should cut the curve in
two consecutive points there. The tangent to the circle at that
point will be the required tangent to the curve. In modern text-books
it is usual to express the condition that two of the points in
which a straight line (such as y = mx + c)
cuts the curve shall coincide with the given point: this enables
us to determine m and c, and thus the equation of
the tangent there is determined. Descartes, however, did not
venture to do this, but selecting a circle as the simplest curve
and one to which he knew how to draw a tangent, he so fixed his
circle as to make it touch the given curve at the point in question,
and thus reduced the problem to drawing a tangent to a circle. I
should note in passing that he only applied this method to curves
which are symmetrical about an axis, and he took the centre of the
circle on the axis.
The obscure style deliberately adopted by Descartes diminished the
circulation and immediate appreciation of these books; but a
Latin translation of them, with explanatory notes, was prepared
by F. de Beaune, and an edition of this, with a commentary by
F. van Schooten, issued in 1659, was widely read.
The third book of the Géométrie contains an
analysis of the algebra then current, and it has affected the
language of the subject by fixing the custom of employing the
letters at the beginning of the alphabet to denote known quantities,
and those at the end of the alphabet to denote unknown
quantities. [On the origin of the custom of using x to
represent an unknown example, see a note by G. Eneström
in the Bibliotheca Mathematica, 1885, p. 43.]
Descartes further introduced the system of indices now in use;
very likely it was original on his part, but I would here remind
the reader that the suggestion had been made by previous writers,
though it had not been generally adopted. It is doubtful whether
or not Descartes recognized that his letters might represent any
quantities, positive or negative, and that it was sufficient to
prove a proposition for one general case. He was the earliest
writer to realise the advantage to be obtained by taking all the
terms of an equation to one side of it, though Stifel and Harriot
had sometimes employed that form by choice. He realised the meaning
of negative quantities and used them freely. In this book he made
use of the rule for finding the limit to the number of positive
and of negative roots of an algebraical equation, which is still
known by his name; and introduced the method of indeterminate
coefficients for the solution of equations. He believed that he
had given a method by which algebraical equations of any order could
be solved, but in this he was mistaken. It may also be mentioned
that he enunciated the theorem, commonly attributed to Euler, on
the relation between the numbers of faces, edges and angles of a
polyhedron: this is in one of the papers published by Careil.
Of the two other appendices to the Discours one was devoted
to optics. The chief interest of this consists in the statement
given of the law of refraction. This appears to have been taken
from Snell's work, though, unfortunately, it is enunciated in a
way which might lead a reader to suppose that it is due to the
researches of Descartes. Descartes would seem to have repeated
Snell's experiments when in Paris in 1626 or 1627, and it is
possible that he subsequently forgot how much he owed to the
earlier investigations of Snell. A large part of the optics is
devoted to determining the best shape for the lenses of a
telescope, but the mechanical difficulties in grinding a surface
of glass to a required form are so great as to render these
investigations of little practical use. Descartes seems to have
been doubtful whether to regard the rays of light as proceeding
from the eye and so to speak touching the object, as the Greeks
had done, or as proceeding from the object, and so affecting the
eye; but, since he considered the velocity of light to be infinite,
he did not deem the point particularly important.
The other appendix, on meteors, contains an explanation
of numerous atmospheric phenomena, including the rainbow; the
explanation of the latter is necessarily incomplete, since
Descartes was unacquainted with the fact that the refractive
index of a substance is different for lights of different colours.
Descartes's physical theory of the universe, embodying most of the
results contained in his earlier and unpublished Le Monde,
is given in his Principia, 1644, and rests on a metaphysical
basis. He commences with a discussion on motion; and then lays down
ten laws of nature, of which the first two are almost identical with
the first two laws of motion as given by Newton; the remaining eight
laws are inaccurate. He next proceeds to discuss the nature of matter
which he regards as uniform in kind though there are three forms of it.
He assumes that the matter of the universe must be in motion, and that
the motion must result in a number of vortices. He states that the sun
is the centre of an immense whirlpool of this matter, in which the
planets float and are swept round like straws in a whirlpool of water.
Each planet is supposed to be the centre of a secondary whirlpool by
which its satellites are carried: these secondary whirlpools are
supposed to produce variations of density in the surrounding medium
which constitute the primary whirlpool, and so cause the planets to
move in ellipses and not in circles. All these assumptions are
arbitrary and unsupported by any investigation. It is not difficult
to prove that on his hypothesis the sun would be in the centre of
these ellipses, and not at a focus (as Kepler had shewn was the case),
and that the weight of a body at every place on the surface of the
earth except the equator would act in a direction which was not
vertical; but it will be sufficient here to say that Newton in the
second book of his Principia, 1687, considered the theory in
detail, and shewed that its consequences are not only inconsistent
with each of Kepler's laws and with the fundamental laws of mechanics,
but are also at variance with the laws of nature assumed by Descartes.
Still, in spite of its crudeness and its inherent defects, the theory
of vortices marks a fresh era in astronomy, for it was an attempt to
explain the phenomena of the whole universe by the same mechanical laws
which experiment shews to be true on the earth.
This page is included in a
collection of mathematical biographies taken from
A Short Account of the History of Mathematics
by W. W. Rouse Ball (4th Edition, 1908).
Transcribed by
D.R. Wilkins
(dwilkins@maths.tcd.ie)
School of Mathematics
Trinity College, Dublin
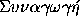 and of which some particular cases had been considered by Euclid
and Apollonius. The general theorem had baffled previous
geometricians, and it was in the attempt to solve it that Descartes
was led to the invention of analytical geometry. The full enunciation
of the problem is rather involved, but the most important case is
to find the locus of a point such that the product of the perpendiculars
on m given straight lines shall be in a constant ratio to
the product of the perpendiculars on n other given straight
lines. The ancients had solved this geometrically for the case
m = 1, n = 1, and the case m = 1, n = 2.
Pappus had further stated that, if m = n = 2, the
locus is a conic, but he gave no proof; Descartes also failed to
prove this by pure geometry, but he shewed that the curve is
represented by an equation of the second degree, that is, a conic;
subsequently Newton gave an elegant solution of the problem by pure
geometry.
and of which some particular cases had been considered by Euclid
and Apollonius. The general theorem had baffled previous
geometricians, and it was in the attempt to solve it that Descartes
was led to the invention of analytical geometry. The full enunciation
of the problem is rather involved, but the most important case is
to find the locus of a point such that the product of the perpendiculars
on m given straight lines shall be in a constant ratio to
the product of the perpendiculars on n other given straight
lines. The ancients had solved this geometrically for the case
m = 1, n = 1, and the case m = 1, n = 2.
Pappus had further stated that, if m = n = 2, the
locus is a conic, but he gave no proof; Descartes also failed to
prove this by pure geometry, but he shewed that the curve is
represented by an equation of the second degree, that is, a conic;
subsequently Newton gave an elegant solution of the problem by pure
geometry.