
From `A Short Account of the History of Mathematics' (4th edition, 1908) by W. W. Rouse Ball.
William, Viscount Brouncker, one of the founders of the Royal Society of London, born about 1620, and died on April 5, 1684, was among the most brilliant mathematicians of this time, and was in intimate relations with Wallis, Fermat, and other leading mathematicians. I mentioned above his curious reproduction of Brahmagupta's solution of a certain indeterminate equation. Brouncker proved that the area enclosed between the equilateral hyperbola xy = 1, the axis of x, and the ordinates x = 1 and x = 2, is equal either to
or to
He also worked out other similar expressions for different areas bounded by the hyperbola and straight lines. He wrote on the rectification of the parabola and of the cycloid. It is noticeable that he used infinite series to express quantities whose values he could not otherwise determine. In answer to a request of Wallis to attempt the quadrature of the circle he shewed that the ratio of the area of a circle to the area of the circumscribed square, that is, the ratio of
 to 4, is equal to the ratio of
to 4, is equal to the ratio of
to 1. Continued fractions had been employed by Bombelli in 1572, and had been systematically used by Cataldi in his treatise on finding the square roots of numbers, published at Bologna in 1613. Their properties and theory were given by Huygens, 1703 and Euler, 1744.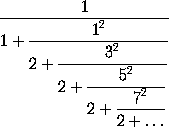
This page is included in a collection of mathematical biographies taken from A Short Account of the History of Mathematics by W. W. Rouse Ball (4th Edition, 1908).
Transcribed by