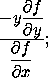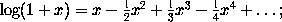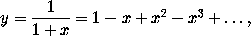Some Contemporaries of Descartes, Fermat, Pascal and Huygens
From `A Short Account of the History of Mathematics' (4th edition, 1908)
by W. W. Rouse Ball.
Bachet |
Mersenne |
Roberval |
Van Schooten |
Saint-Vincent |
Torricelli |
Hudde |
Frénicle |
De Laloubère |
N. Mercator |
Wren |
Hooke |
Collins |
Pell |
Sluze |
Viviani |
Tchirnhausen |
De la Hire |
Roemer |
Rolle
Claude Gaspard Bachet de Méziriac was born at Bourg in
1581, and died in 1638. He wrote the Problèmes plaisants,
of which the first edition was issued in 1612, a second and enlarged
edition was brought out in 1624; this contains an interesting
collection of arithmetical tricks and questions, many of which are
quoted in my Mathematical Recreations and Essays. He also wrote
Les éléments arithmétiques, which exists in manuscript;
and a translation of the Arithmetic of Diophantus. Bachet was
the earliest writer who discussed the solution of indeterminate equations
by means of continued fractions.
Marin Mersenne, born in 1588 and died at Paris in 1648, was a
Franciscan friar, who made it his business to be acquainted and
correspond with the French mathematicians of that date and many
of their foreign contemporaries. In 1634 he published a translation
of Galileo's mechanics; in 1644 he issued his
Cogita Physico-Mathematica, by which he is best known, containing
an account of some experiments in physics; he also wrote a synopsis
of mathematics, which was printed in 1664.
The preface to the Cogitata contains a statement
(possibly due to Fermat) that, in order that
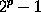 may be prime,
the only values of p, not greater than 257, which are possible
are 1, 2, 3, 5, 7, 13, 17, 19, 31, 67, 127, and 257; the number 67
is probably a misprint for 61. With this correction the statement
appears to be true, and it has been verified for all except twenty-one
values of p, namely 71, 89, 101, 103, 107, 109, 127, 137,
139, 149, 157, 163, 167, 173, 181, 193, 199, 227, 229, 241, and
257. Of these values, Mersenne asserted that p = 127 and
p = 257 make
may be prime,
the only values of p, not greater than 257, which are possible
are 1, 2, 3, 5, 7, 13, 17, 19, 31, 67, 127, and 257; the number 67
is probably a misprint for 61. With this correction the statement
appears to be true, and it has been verified for all except twenty-one
values of p, namely 71, 89, 101, 103, 107, 109, 127, 137,
139, 149, 157, 163, 167, 173, 181, 193, 199, 227, 229, 241, and
257. Of these values, Mersenne asserted that p = 127 and
p = 257 make
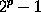 prime, and that the other nineteen
values make
prime, and that the other nineteen
values make
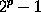 a composite number. It has been asserted
that the statement has been verified when p = 89 and 127,
but these verifications rest on long numerical calculations made
by single computators and not published; until these demonstrations
have been confirmed we may say that twenty-one cases still await
verification or require further investigation. The factors of
a composite number. It has been asserted
that the statement has been verified when p = 89 and 127,
but these verifications rest on long numerical calculations made
by single computators and not published; until these demonstrations
have been confirmed we may say that twenty-one cases still await
verification or require further investigation. The factors of
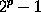 when p = 89 are not known, the calculation merely
showing that the number could not be prime. It is most likely that
these results are particular cases of some general theorem on the
subject which remains to be discovered.
when p = 89 are not known, the calculation merely
showing that the number could not be prime. It is most likely that
these results are particular cases of some general theorem on the
subject which remains to be discovered.
The theory of perfect numbers depends directly on that of Mersenne's
numbers. It is probable that all perfect numbers are included in the
formula
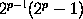 ,
where
,
where
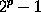 is a prime. Euclid proved
that any number of this form is perfect. Euler shewed that the formula
includes all even perfect numbers; and there is reason to
believe - though a rigid demonstration is wanting - that an odd number
cannot be perfect. If we assume that the last of these statements
is true, then every perfect number is of the above form. Thus if
p = 2, 3, 5, 7, 13, 17, 19, 31, 61, then, by Mersenne's rule,
the corresponding values of
is a prime. Euclid proved
that any number of this form is perfect. Euler shewed that the formula
includes all even perfect numbers; and there is reason to
believe - though a rigid demonstration is wanting - that an odd number
cannot be perfect. If we assume that the last of these statements
is true, then every perfect number is of the above form. Thus if
p = 2, 3, 5, 7, 13, 17, 19, 31, 61, then, by Mersenne's rule,
the corresponding values of
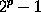 are prime; they are 3, 7, 31, 127, 8191, 131071, 524287, 2147483647,
2305843009213693951; and the corresponding perfect numbers are
6, 28, 496, 8128, 33550336, 8589869056, 137438691328,
2305843008139952128, and 2658455991569831744654692615953842176.
are prime; they are 3, 7, 31, 127, 8191, 131071, 524287, 2147483647,
2305843009213693951; and the corresponding perfect numbers are
6, 28, 496, 8128, 33550336, 8589869056, 137438691328,
2305843008139952128, and 2658455991569831744654692615953842176.
Gilles Personier (de) Roberval, born at Roberval in 1602 and
died at Paris in 1675, described himself from the place of his birth
as de Roberval, a seigniorial title to which he had no right. He
discussed the nature of the tangents to curves, solved some of the
easier questions connected with the cycloid, generalized Archimedes's
theorems on the spiral, wrote on mechanics, and on the method of
indivisibles, which he rendered more precise and logical. He was
a professor in the university of Paris, and in correspondence with
nearly all the leading mathematicians of his time.
Frans van Schooten, to whom we owe an edition of Vieta's works,
succeeded his father (who had taught mathematics to Huygens, Hudde,
and Sluze) as professor at Leyden in 1646. He brought out in 1659
a Latin translation of Descartes's Géométrie, and in
1657 a collection of mathematical exercises in which he recommended
the use of co-ordinates in space of three dimensions. He died in 1661.
Grégoire de Saint-Vincent, a Jesuit, born at Bruges
in 1584 and died at Ghent in 1667, discovered the expansion of
log(1 + x) in ascending powers of x. Although a
circle-squarer he is worthy of mention for the numerous theorems
of interest which he discovered in his search after the impossible,
and Montucla ingeniously remarks that ``no one ever squared the
circle with so much ability or (except for his principal object)
with so much success.'' He wrote two books on the subject, one
published in 1647 and the other in 1668, which cover some two or
three thousand closely printed pages; the fallacy in the quadrature
was pointed out by Huygens. In the former work he used indivisibles.
An earlier work entitled Theoremata Mathematica,
published in 1624, contains a clear account of the method of
exhaustions, which is applied to several quadratures, notably that
of the hyperbola.
Evangelista Torricelli, born at Faenza on Oct. 15, 1608, and died
at Florence in 1647, wrote on the quadrature of the cycloid and conics;
the rectifications of the logarithmic spiral; the theory of the barometer;
the value of gravity found by observing the motion of two weights
connected by a string passing over a fixed pulley; the theory of
projectiles; and the motion of fluids.
Johann Hudde, burgomaster of Amsterdam, was born there in
1633, and died in the same town in 1704. He wrote two tracts in
1659: one was on the reduction of equations which have equal roots;
in the other he stated what is equivalent to the proposition that
if f(x,y) = 0 be the algebraical equation of a curve,
then the subtangent is
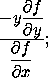
but being ignorant of the notation of the calculus his enunciation
is involved.
Bernard Frénicle de Bessy, born in Paris circ. 1605 and died
in 1670, wrote numerous papers on combinations and on the theory of
numbers, also on magic squares. It may be interesting to add that he
challenged Huygens to solve the following system of equations in
integers,
x² + y² = z²,
x² = u² + v²,
x - y = u - v.
A solution was given by M. Pépin in 1880.
Antoine de Laloubère, a Jesuit, born in Languedoc in 1600
and died at Toulouse in 1664, is chiefly celebrated for an incorrect
solution of Pascal's problems on the cycloid, which he gave in 1660,
but he has a better claim to distinction in having been the first
mathematician to study the properties of the helix.
Nicholas Mercator (sometimes known as Kauffmann)
was born in Holstein about 1620, but resided most of his life in
England. He went to France in 1683, where he designed and constructed
the fountains at Versailles, but the payment agreed on was refused
unless he would turn Catholic; he died of vexation and poverty in
Paris in 1687. He wrote a treatise on logarithms entitled
Logarithmo-technica, published in 1668, and discovered the series
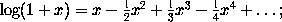
he proved this by writing the equation of a hyperbola in the form
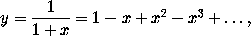
to which Wallis's method of quadrature could be applied. The same
series had been independently discovered by Saint-Vincent.
Sir Christopher Wren was born at Knoyle, Wiltshire, on
October 20, 1632, and died in London on February 25, 1723. Wren's
reputation as a mathematician has been overshadowed by his fame as
an architect, but he was Savilian professor of astronomy at Oxford
from 1661 to 1673, and for some time president of the Royal Society.
Together with Wallis and Huygens he investigated the laws of collision
of bodies; he also discovered the two systems of generating lines on
the hyperboloid of one sheet, though it is probable that he confined
his attention to a hyperboloid of revolution.
Besides these he wrote papers on the resistance of fluids, and the
motion of the pendulum. He was a friend of Newton and (like Huygens,
Hooke, Halley, and others) had made attempts to shew that the force
under which the planets move varies inversely as the square of the
distance from the sun.
Wallis, Brouncker, Wren, and Boyle (the last-named being a chemist
and physicist rather than a mathematician) were the leading
philosophers who founded the Royal Society of London. The society
arose from the self-styled ``indivisible college'' in London in 1645;
most of its members moved to Oxford during the civil war, where
Hooke, who was then an assistant in Boyle's laboratory, joined in
their meetings; the society was formally constituted in London in
1660, and was incorporated on July 15, 1662. The French Academy was
founded in 1666, and the Berlin Academy in 1700. The Accademia
dei Lincei was founded in 1603, but was dissolved in 1630.
Robert Hooke, born at Freshwater on July 18, 1635, and died
in London on March 3, 1703, was educated at Westminster, and
Christ Church, Oxford, and in 1665 became professor of geometry
at Gresham College, a post which he occupied till his death.
He is still known by the law which he discovered, that the tension
exerted by a stretched string is (within certain limits) proportional
to the extension, or, in other words, that the stress is proportional
to the strain. He invented and discussed the conical pendulum, and was
the first to state explicitly that the motions of the heavenly bodies
were merely dynamical problems. He was as jealous as he was vain and
irritable, and accused both Newton and Huygens of unfairly
appropriating his results. Like Huygens, Wren, and Halley, he made
efforts to find the law of force under which the planets move about
the sun, and he believed the law to be that of the inverse square
of the distance. He, like Huygens, discovered that the small
oscillations of a coiled spiral spring were practically isochronous,
and was thus led to recommend (possibly in 1658) the use of the
balance spring in watches. He had a watch of this kind made in
London in 1675; it was finished just three months later than a
similar one made in Paris under the directions of Huygens.
John Collins, born near Oxford on March 5, 1625, and died
in London on November 10, 1683, was a man of great natural
ability, but of slight education. Being devoted to mathematics,
he spent his spare time in correspondence with the leading
mathematicians of the time, for whom he was always ready
to do anything in his power, and he has been described - not
inaptly - as the English Mersenne. To him we are indebted for
much information on the details of the discoveries of the
period.
Another mathematician who devoted a considerable part of his
time to making known the discoveries of others, and to
correspondence with leading mathematicians, was John Pell.
Pell was born in Sussex on March 1, 1610, and died in London on
December 10, 1685. He was educated at Trinity College, Cambridge;
he occupied in succession the mathematical chairs at Amsterdam and
Breda; he then entered the English diplomatic service; but finally
settled in 1661 in London, where he spent the last twenty years of
his life. His chief works were an edition, with considerable new
matter, of the Algebra by Branker and Rhonius, London, 1668;
and a table of square numbers, London, 1672.
René François Walther de Sluze (Slusius),
canon of Liége, born on July 7, 1622, and died on March 19,
1685, found for the subtangent of a curve f(x,y) = 0 an
expression which is equivalent to
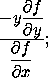
he wrote numerous tracts, and in particular discussed at some
length spirals and points of inflexion.
Vincenzo Viviani, a pupil of Galileo and Torricelli, born at
Florence on April 5, 1622, and died there on September 22, 1703,
brought out in 1659 a restoration of the lost book of Apollonius
on conic sections, and in 1701 a restoration of the work of
Aristaeus. He explained in 1677 how an angle could be trisected
by the aid of the equilateral hyperbola or the conchoid. In 1692
he proposed the problem to construct four windows in a hemispherical
vault so that the remainder of the surface can be accurately determined;
a celebrated problem, of which analytical solutions were given by
Wallis, Leibnitz, David Gregory, and James Bernoulli.
Ehrenfried Walther von Tschirnhausen was born at
Kislingswalde on April 10, 1631, and died at Dresden on
October 11, 1708. In 1682 he worked out the theory of
caustics by reflexion, or, as they were usually called,
catacaustics, and shewed that they were rectifiable.
This was the second case in which the envelope of a moving
line was determined. He constructed burning mirrors of
great power. The transformation by which he removed certain
intermediate terms from a given algebraical equation is
well known; it was published in the Acta Eruditorum
for 1683.
Philippe De la Hire (or Lahire), born in Paris
on March 18, 1640, and died there on April 21, 1719, wrote on
graphical methods, 1673; on the conic sections, 1685; a
treatise on epicycloids, 1694; one on roulettes, 1702; and,
lastly, another on conchoids, 1708. His works on conic sections
and epicycloids were founded on the teaching of Desargues, whose
favourite pupil he was. He also translated the essay of
Moschopulus on magic squares, and collected many of the
theorems on them which were previously known; this was
published in 1705.
Ole Roemer, born at Aarhuus on September 25, 1644, and died
at Copenhagen on September 19, 1710, was the first to measure the
velocity of light; this was done in 1675 by means of the eclipses
of Jupiter's satellites. He brought the transit and mural circle
into common use, the altazimuth having been previously generally
employed, and it was on his recommendation that astronomical
observations of stars were subsequently made in general on the
meridian. He was also the first to introduce micrometers and
reading microscopes into an observatory. He also deduced from the
properties of epicycloids the form of the teeth in toothed-wheels
best fitted to secure a uniform motion.
Michel Rolle, born at Ambert on April 21, 1652, and died in
Paris on November 8, 1719, wrote an algebra in 1689, which contains
the theorem on the position of the roots of an equation which is
known by his name. He published in 1696 a treatise on the
solutions of equations, whether determinate or indeterminate, and
he produced several other minor works. He taught that the
differential calculus, which, as we shall see later, had been
introduced towards the close of the seventeenth century, was nothing
but a collection of ingenious fallacies.
This page is included in a
collection of mathematical biographies taken from
A Short Account of the History of Mathematics
by W. W. Rouse Ball (4th Edition, 1908).
Transcribed by
D.R. Wilkins
(dwilkins@maths.tcd.ie)
School of Mathematics
Trinity College, Dublin
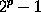 may be prime,
the only values of p, not greater than 257, which are possible
are 1, 2, 3, 5, 7, 13, 17, 19, 31, 67, 127, and 257; the number 67
is probably a misprint for 61. With this correction the statement
appears to be true, and it has been verified for all except twenty-one
values of p, namely 71, 89, 101, 103, 107, 109, 127, 137,
139, 149, 157, 163, 167, 173, 181, 193, 199, 227, 229, 241, and
257. Of these values, Mersenne asserted that p = 127 and
p = 257 make
may be prime,
the only values of p, not greater than 257, which are possible
are 1, 2, 3, 5, 7, 13, 17, 19, 31, 67, 127, and 257; the number 67
is probably a misprint for 61. With this correction the statement
appears to be true, and it has been verified for all except twenty-one
values of p, namely 71, 89, 101, 103, 107, 109, 127, 137,
139, 149, 157, 163, 167, 173, 181, 193, 199, 227, 229, 241, and
257. Of these values, Mersenne asserted that p = 127 and
p = 257 make
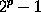 prime, and that the other nineteen
values make
prime, and that the other nineteen
values make
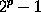 a composite number. It has been asserted
that the statement has been verified when p = 89 and 127,
but these verifications rest on long numerical calculations made
by single computators and not published; until these demonstrations
have been confirmed we may say that twenty-one cases still await
verification or require further investigation. The factors of
a composite number. It has been asserted
that the statement has been verified when p = 89 and 127,
but these verifications rest on long numerical calculations made
by single computators and not published; until these demonstrations
have been confirmed we may say that twenty-one cases still await
verification or require further investigation. The factors of
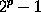 when p = 89 are not known, the calculation merely
showing that the number could not be prime. It is most likely that
these results are particular cases of some general theorem on the
subject which remains to be discovered.
when p = 89 are not known, the calculation merely
showing that the number could not be prime. It is most likely that
these results are particular cases of some general theorem on the
subject which remains to be discovered.
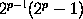 ,
where
,
where